1. Pengantar dan Defenisi Vektor

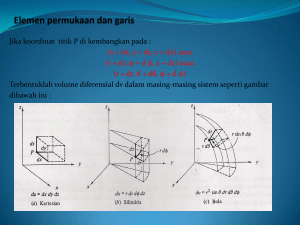
 1. Pengantar Lingkaran adalah kumpulan titik titik yang jaraknya sama dari suatu titik yang disebut pusat lingkaran Jarak adalah besaran skalar yaitu besaran yang hanya mempunyai nilai Titik 𝐴 dan titik 𝐵 pada lingkaran sama jaraknya dari pusat lingkaran 𝑂 0,0 Gambar 1 Lantas apa yang membedakan atau bagaimana membedakan titik 𝐴 dan titik 𝐵? Kedua titik dibedakan dari arahnya terhadap pusat lingkaran 𝑂 0,0 dan sumbu 𝑋 positif Titik 𝐴 membentuk sudut 𝛼 dengan sumbu 𝑋 positif Titik 𝐵 membentuk sudut 𝛽 dengan sumbu 𝑋 positif Pada sistem koordinat Polar letak suatu titik terhadap pusat sumbu 𝑂 0,0 ditulis 𝑟 cos 𝛼 , 𝑟 sin 𝛼 dimana 𝑟 adalah jarak titik terhadap pusat sumbu 𝑂 0,0 𝛼 adalah sudut antara garis yang menghubungkan titik pusat 𝑂 0,0 dan titik pada lingkaran dengan sumbu 𝑋 positif Pada sistem koordinat Cartesius letak suatu titik terhadap pusat sumbu 𝑂 0,0 ditulis 𝑥, 𝑦 Dimana 𝑥 adalah jarak titik ke sumbu 𝑌 𝑦 adalah jarak titik ke sumbu 𝑋 Hubungan antara sistem koordinat Polar dan Cartesius 𝑥 = 𝑟 cos 𝛼 dan 𝑦 = 𝑟 sin 𝛼 Gambar 2 Letak titik 𝐴 relatif terhadap titik 𝑂 adalah 𝑥 ke kanan dan 𝑦 ke atas Panjang atau jarak 𝑂𝐴 atau jari jari lingkaran adalah 𝑑=𝑟=
𝑥 ! + 𝑦 ! 2. Defenisi Vektor Vektor adalah besaran yang mempunyai nilai dan arah Vektor satuan adalah vektor yang panjangnya sama dengan 1 Vektor posisi suatu titik adalah vektor yang awalnya adalah titik 𝑂 0,0 dan ujungnya titik 𝐴 𝑥, 𝑦 Vektor digambarkan dengan garis berpanah dari titik awal ke titik akhir Pada gambar 3 titik awal adalah titik 𝑂 0,0 dan titik akhir adalah titik 𝐴 𝑥, 𝑦 Vektor dilambangkan dengan ruas garis 𝑂𝐴 atau 𝑎 atau 𝑎 Gambar 3 Pada sistem koordinat Cartesius vektor posisi titik 𝐴 𝑥, 𝑦 ditulis 𝑥
𝑂𝐴 = 𝑎 = 𝑎 = 𝑦 = 𝑥ı + 𝑦ȷ dimana 1
ı adalah vektor satuan dalam arah horisontal 0
0
ȷ adalah vektor satuan dalam arah vertikal 1
Dengan menggunakan prinsip Pythagoras pada segitiga siku siku dan gradien pada garis lurus maka 𝑥
Panjang vektor 𝑂𝐴 = 𝑦 = 𝑥ı + 𝑦ȷ adalah 𝑂𝐴 = 𝑎 = 𝑎 =
𝑥 ! + 𝑦 ! Arah atau gradien vektor 𝑂𝐴 adalah 𝑚 = tan 𝛼 =
𝑦
𝑥
3. Sifat Sifat Vektor a. Kesamaan Vektor Vektor 𝑎 = 𝑥! ı + 𝑦! ȷ dikatakan sama dengan vektor 𝑏 = 𝑥! ı + 𝑦! ȷ jika dan hanya jika panjang dan arahnya sama atau 𝑥! = 𝑥! dan 𝑦! = 𝑦! dan ditulis 𝑎 = 𝑏 . Titik awal kedua vektor tidak perlu sama Dua vektor yang sama bisa sejajar, segaris dan berhimpit Gambar 4 Perhatikan jajaran genjang 𝐴𝐵𝐶𝐷 dimana dua pasang sisi sama panjang dan sejajar serta diagonal berpotongan di tengah tengah maka 𝐴𝐷 = 𝐵𝐶 dan 𝐴𝐷 ∥ 𝐵𝐶 sehingga 𝐴𝐷 = 𝐵𝐶 𝐴𝑃 = 𝑃𝐶 dan 𝐴𝑃, 𝑃𝐶 segaris pada garis 𝐴𝐶 sehingga 𝐴𝑃 = 𝑃𝐶 b. Vektor Nol Vektor nol adalah vektor yang titik awal dan akhirnya sama Panjangnya sama dengan nol dan arahnya sama seandainya tidak nol dan ditulis 𝐴𝐴 atau 0 c. Vektor Lawan atau Negatif Suatu Vektor Vektor 𝑏 = 𝑥! ı + 𝑦! ȷ dikatakan lawan atau negatif dari vektor 𝑎 = 𝑥! ı +
𝑦! ȷ adalah jika dan hanya jika besarnya sama 𝑎 = 𝑏 tetapi arahnya berlawanan dan ditulis 𝑏 = −𝑎 atau 𝑥! ı + 𝑦! ȷ = −𝑥! ı − 𝑦! ȷ Pada gambar vektor 𝐷𝑃 = 𝐵𝑃 dan segaris tetapi berlawanan arah maka 𝐷𝑃 = −𝐵𝑃