Elemen permukaan dan garis

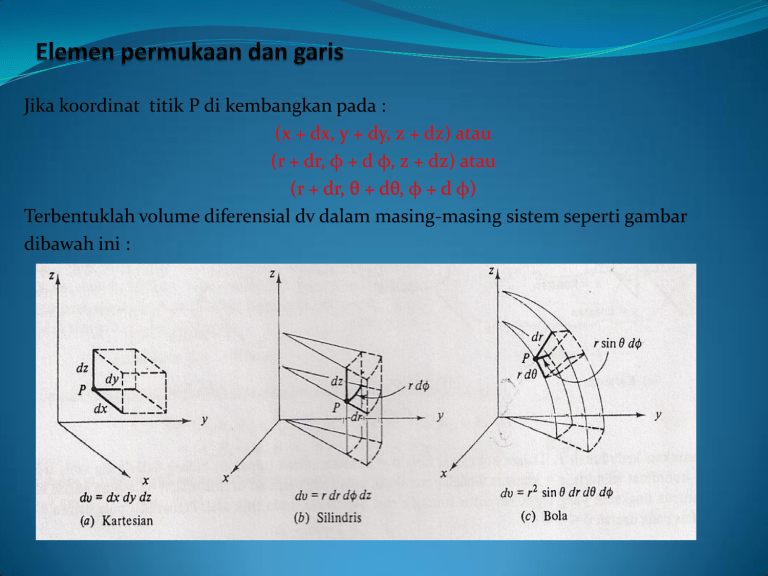
Jika koordinat titik P di kembangkan pada :
(x + dx, y + dy, z + dz) atau
(r + dr, φ + d φ, z + dz) atau
(r + dr, θ + dθ, φ + d φ)
Terbentuklah volume diferensial dv dalam masing-masing sistem seperti gambar
dibawah ini :
Dari gambar di atas dapat pula dibaca luas elemen-elemen permukaan yang
membatasi volume diferensial tadi. Sebagai contoh elemen luas pemukaan
koordinat bola yang tegak lurus
:
dS = (r dθ)(r sin θ d φ) = r² sin sin θ dθ d φ
Elemen garis diferensial dl adalah diagonal yang melalui P :
dl² = dx² + dy² + dz²
kartesian
dl² = dr² + r² dφ² + dz²
silindris
dl² = dr² + r² dθ² + r² sin θ dφ
bola
MEDAN VEKTOR
Medan vektor dalam teori elektromagnetik pada umumnya adalah koefisien vektor
satuan yang mengandung fungsi koordinat-koordinatnya. Oleh karena itu, ia akan
berubah nilai dan arahnya pada satu titik ke titik lain dalam daerah yang ditinjau.
Misal :
E = - x ax + yay
Nilai-nilai x dan y disubstitusikan ke dalam ungkapan tersebut untuk memberikan
E pada tempat-tempat yang berdeda. Setelah di coba beberapa titik, polanya jelas
seperti gambar di bawah ini :
disamping itu, suatu medan vektor dapat berubah dengan waktu. Maka suatu
medan berdimensi dua dapat diberikan perubahan waktu, misalnya :
E = (-x ax + y ay) sin ωt
Atau
E = (-x ax + y ay) eiωt
TRANSFORMASI
Vektor atau medan vektor di dalam suatu persoalan secara fisik memang ada,
sedangkan koordinat yang dipakai untuk mengungkapkannya hanyalah suatu
kerangka acuan saja.
Sehingga kita dapat mentransformasikan suatu koordinat ke koordinat lain.
- dari koordinat kartesian ke koordinat bola, begitu sebaliknya
- dari koordinat kartesian ke koordinat silindris, begitu sebaliknya
- dari koordinar silindris ke koordinat bola, begitu sebaliknya.
Contoh : A = 5 rar + 2 sin φ aθ + 2 cos θ aφ
Dalam koordinat bola. Variabel r, θ, φ dapat diubah menjadi variabel kartesian
dengan mengacu pada gambar :
Dan menerapkan trigonometri dasar. Maka :
Demikian pula komponen-komponen koordinat bola dari medan vektor A dapa
dituliskan dalam x, y, z
ar +
aθ +
aφ
Vektor satuan ar , aθ , aφ juga dapat ditransformasikan ke dalam ekivalensi
kartesiannya, lagi dengan mengacu pada gambar :
Dan menerapkan trigonometri dasar, maka :
ar =
ax +
ay +
az
aθ =
ax +
aφ =
ax +
ay -
az
ay
dengan mengkombinasikan diperoleh :
A=
ax
+
ay +
az