BAB II VEKTOR DAN GERAK DALAM RUANG

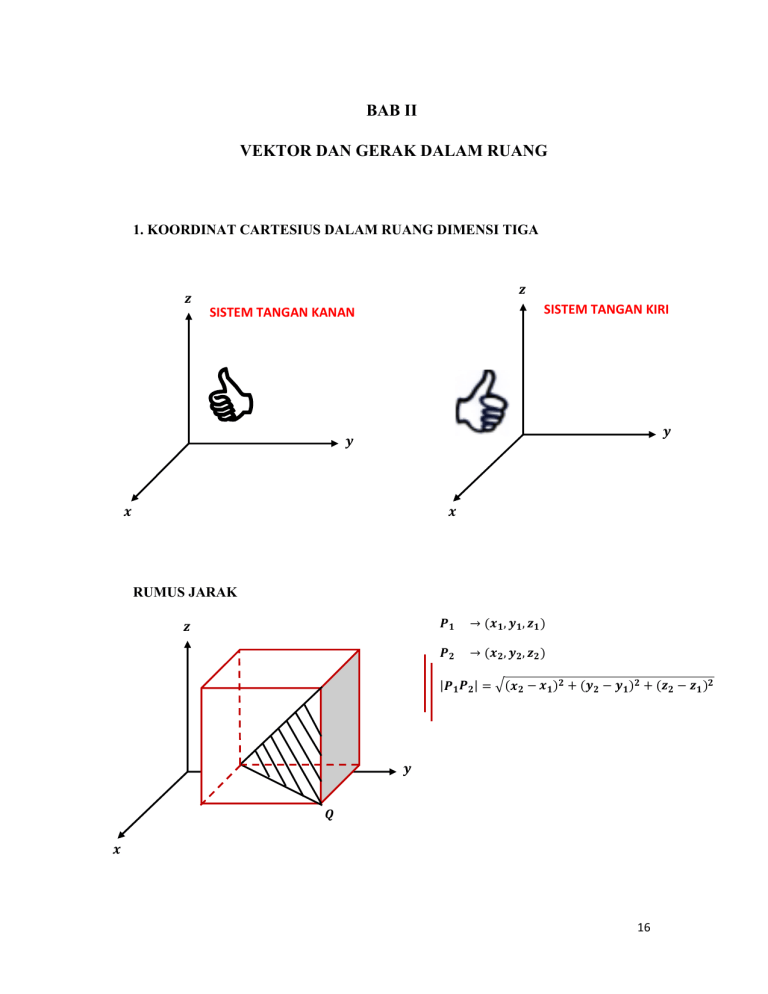
BAB II
VEKTOR DAN GERAK DALAM RUANG
1. KOORDINAT CARTESIUS DALAM RUANG DIMENSI TIGA
SISTEM TANGAN KIRI SISTEM TANGAN KANAN &
RUMUS JARAK
|
,
,
,
,
|
16 Contoh : Carilah jarak antara titik
Solusi : |
,
,
, ,
dan
|
.
,
√
Persamaan baku sebuah bola
Jika
, ,
pada bola dengan radius
, , , maka :
berpusat pada
atau dalam bentuk terurai dapat ditulis sebagai
Contoh : Carilah pusat dan radius bola dengan persamaan :
Solusi :
Pusat bola
, ,
; radius
GRAFIK DALAM RUANG DIMENSI TIGA
Contoh : Gambarkanlah grafik dari
Solusi : Perpotongan dengan sumbu
ambil
&
0
ambil
&
0
, ,
Perpotongan dengan sumbu
17 , ,
Perpotongan dengan sumbu
, ,
, ,
Bidang , ,
, ,
2. VEKTOR DALAM RUANG DIMENSI TIGA
,
, ,
,
disebut vektor basis. Panjang , diberikan sbb:
adalah vektor satuan baku
| |
,
Bila
,
dan
,
,
; maka
.
dan
.
| || |
18 Contoh :
,
Cari sudut ABC jika
,
,
,
,
, ,
,
dan
,
Vektor
Vektor
, ,
,
.
| || |
,
,
,
,
,
,
,
,
,
√
√
,
,
™ SUDUT DAN KOSINUS ARAH
yang tak nol dengan vektor satuan , ,
Sudut antara vektor
disebut sudut-
sudut arah vektor
, maka :
Jika
.
| || |
| |
;
| |
;
| |
19 Contoh : Cari sudut-sudut arah vektor
Solusi : | |
√
√
√
√
;
√
;
,
,
,
Contoh : Cari vektor yang panjangnya 5 satuan yang mempunyai
,
Solusi :
,
Vektor yang memenuhi persyaratan :
,
,
,
,
,
,
,
,
,
, ,
,
,
,
,
,
dan
,
™ BIDANG
Bila
, ,
adalah sebuah vektor tak nol tetap dan
titik tetap. Himpunan semua titik
BIDANG yang melalui
,
Maka,
.
, ,
yang memenuhi
,
,
.
adalah
adalah
dan tegak lurus .
,
setara terhadap
Persamaan ini (paling sedikit salah satu A,B,C tidak nol) disebut bentuk baku
persamaan bidang.
20 Persamaan diatas dapat disederhanakan menjadi :
,
Contoh:
Cari persamaan bidang yang melalui
, ,
, ,
tegak lurus terhadap
. Kemudian cari sudut antara bidang ini dan bidang yang persamaannya
Solusi :
Vektor
,
terhadap bidang kedua adalah
,
. Sudut
antara dua
bidang tersebut adalah :
.
| || |
√
√
,
,
3. HASIL KALI SILANG
Hasil kali silang (hasil kali vektor atau cross product),
dan
,
,
untuk
,
,
didefinisikan sebagai
,
,
Untuk memudahkan, gunakan pengertian determinan
21 Dengan determinan,
hukum anti komutatif
,
Contoh : Andaikan
Hitunglah
dan
,
dan
, ,
menggunakan definisi determinan
Solusi :
Teorema :
Andaikan
dan
vektor-vektor dalam ruang dimensi tiga dan
sudut antara
mereka, Maka :
1. .
2. |
.
|
terhadap ,
| || |
3. Dua vektor
dan
dalam ruang dimensi tiga adalah sejajar jika dan hanya jika
22 Contoh : Cari persamaan bidang yang melalui tiga titik
,
,
,
, ,
,
,
,
Solusi :
,
,
dan
,
,
Maka,
Bidang yang melalui
, ,
dengan normal
mempunyai
persamaan :
atau
™ SIFAT-SIFAT ALJABAR
TEOREMA :
Jika , dan
adalah vektor dalam ruang dimensi tiga dan
skalar, maka :
1.
2.
3.
4.
5. (
6.
23 4. Garis dan Kurva dalam Ruang Dimensi Tiga
Suatu kurva ruang ditentukan oleh suatu tiga persamaan parameter,
,
,
,
, ,
kontinue pada selang I
Suatu kurva dinyatakan dengan cara
memberikan vektor posisi
dari
.
suatu titik
,
,
™ GARIS
garis ditentukan oleh suatu titik tetap
.
dan suatu vector
Garis adalah himpunan semua titik
sedemikian sehingga
adalah sejajar
terhadap ,
;
bilangan riil
dan
Bila
, ,
dan
,
,
,
,
Merupakan persamaan parameter dari garis melalui
, ,
; , ,
,
,
dan sejajar
bilangan-bilangan arah
24 Contoh : Cari persamaan parameter untuk garis yang melalui
,
,
dan
, ,
Solusi :
,
Pilih
,
,
,
sebagai
, ,
,
,
,
,
, maka persamaan parameter :
,
,
, ,
Persamaan simetris garis yang melalui
,
,
dengan bilangan arah a,b,c
yakni :
Persamaan tersebut merupakan konjungsi dari dua persamaan
dan
Contoh : Cari persamaan simetri dari garis yang sejajar vektor
melalui
,
,
dan
, ,
Solusi :
Contoh : Cari persamaan simetri dari garis potong bidang-bidang
dan
Solusi : pilih garis menembus bidang
dan
dan
Menghasilkan titik (0,4,2)
titik , ,
25 vektornya adalah :
,
,
,
,
Dengan menggunakan (3,0,4) untuk
, ,
, ,
,
,
diperoleh :
Contoh : Cari persamaan simetri atau persamaan parameter dari garis yang melalui
(1,-2,3) yang tegaklurus terhadap sumbu x dan garis
Solusi : Sumbu x dan garis yang diberikan arah
, ,
Suatu vektor yang tegak lurus terhadap
dan v :
Garis yang disyaratkan adalah sejajar terhadap
dan
,
,
,
,
Persamaan parameter :
,
,
™ GARIS SINGGUNG PADA KURVA
vektor posisi
,
, dan
adalah
bilangan-bilangan singgung pada
26 Contoh : Cari persamaan simetrik untuk garis singgung pada
, , ⁄
di
Solusi :
Garis singgung mempunyai arah
, ,
.
Persamaan simetriknya adalah :
™ KECEPATAN, PERCEPATAN, dan KELENGKUNGAN
.
Bila
adalah vektor posisi untuk titik
yang menjelajahi kurva selama bertambah besar.
Misalkan
ada dan kontinu dan
dari
ke
kurva mulus. Panjang busur
diberikan oleh
|
|
Jika
waktu
Kecepatan
Percepatan
Laju
|
|
|
|
Contoh :
Suatu titik
bergerak sedemikian hingga vector posisinya pada saat adalah
27 heliks melingkar
•
Cari panjang busur untuk
•
Hitung percepatan
pada
Solusi :
•
Panjang busur
•
™ KELENGKUNGAN
Vektor singgung satuan pada
adalah
|
|
laju perubahan arah garis singgung terhadap jarak sepanjang kurva
|
Kelengkungan
|
dari suatu kurva ruang
|
|
|
|
Contoh : Cari kelengkungan dari heliks melingkar
Solusi :
|
|
|
|
|
|
√
|
|
28 ™ KOMPONEN PERCEPATAN
Vektor normal satuan utama N di P :
⁄
|
⁄
|
adalah normal ( ) terhadap kurva diperoleh dari diferensial .
sehingga
;
.
tegak lurus pada T.
.
.
.
| |
Jika hasil kali silang
|
.
|
Sehingga
|
|
|
|
| || |
atau
|
|
|
|
| |
| |
⁄
Karena
; maka :
|
|
| |
Contoh : pada titik
, ,
, cari , ,
,
, dan
Untuk gerak :
Solusi :
Pada
| |
√
29 | |
√
|
|
| |
√
√
|
√
|
|⁄| |
| |
|
√
√
√
√
√
√
30