Materi Kalkulus 2 : 4 SKS

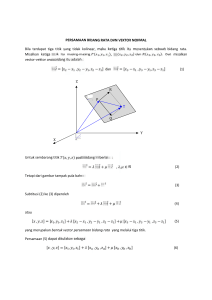
TUJUAN PEMBELAJARAN
Agar pembaca memahami tentang Sistem Koordinat Kartesian beserta
fungsinya yaitu titik, jarak dua titik, persamaan bola serta Vektor
dalam ruang dimensi tiga beserta aplikasinya yaitu sudut antara dua
vektor, persamaan bidang yang dibentuk dari vektor, hasil kali silang
beserta penafsiran secara geometri
OUTCOME PEMBELAJARAN
Setelah mempelajari bab ini diharapkan mahasiswa dapat :
1. Memahami dan mampu menyelesaikan segala permasalahan yang
berkaitan dengan koordinat kartesian dalam ruang dimensi tiga,
antara lain Titik, Jarak dua Titik, Persamaan Bola, Posisi dua
buah Bola, Persamaan Bidang secara Geometri dan Aljabar
2. Memahami dan mampu menyelesaikan Permasalahan yang
berkaitan dengan vektor di Ruang Tiga, yaitu Persamaan Bidang
3. Memahami dan mampu menafsirkan sebuah Hasil Kali Silang dua
vektor beserta penerapannya dalam sebuah bidang
Geometri dalam Ruang, Vektor
129
4.1. Sistem Koordinat Dimensi Tiga
Pada pembahasan yang telah kita lakukan, kita telah memahami dan
belajar pada bidang datar yang dikenal sebagai bidang Euclides atau
ruang dimensi dua hal ini telah diterapkan pada fungsi variable
tunggal yaitu fungsi yang dapat digambarkan pada bidang datar.
Bagaimana jika fungsi yang akan kita pelajari adalah fungsi yang
mempunyai variable ganda atau yang sering kita sebut dengan
kalkulus peubah ganda, yaitu yang diterapkan pada suatu fungsi
yang mempunyai dua peubah atau lebih.
Ambil tiga garis koordinat yang saling tegak lurus, misalnya sumbusumbu X , Y dan Z dengan titik Nol berada pada suatu titik O
yang sama.disebut titik asal. Sistem koordinat dimensi tiga dapat
digambarkan seperti Gambar 4.1
Z
O
X
Y
Gambar 4.1. Sistem Koordinat Dimensi 3
Ketiga sumbu tersebut menentukan tiga bidang, yaitu bidang yz ,
bidang xz dan bidang xy yang membagi ruang menjadi delapan
oktan, Jika titik P dalam ruang, maka koordinat kartesiusnya
dituliskan berupa bilangan ganda tiga yaitu P( x, y, z )
Dalam sistem koordinat dimensi tiga terbagi atas tiga bidang, yaitu :
1. bidang yz yaitu bidang yang tegak lurus sumbu-x
2. bidang xz yaitu bidang yang tegak lurus sumbu-y
3. bidang xy yaitu bidang yang tegak lurus sumbu-z
ketiga bidang tersebut dapat digambarkan seperti Gambar 4.2 berikut
Geometri dalam Ruang, Vektor
130
Z
Z
O
O
Y
Y
X
X
(a) Bidang yz
(b) Bidang xy
Z
O
Y
X
(c) Bidang xz
Gambar 4.2. Tiga Bidang dalam Koordinat Dimensi Tiga
Contoh 4.1 :
Diketahui dua Titik yaitu titik P(2,1,2) dan titik Q(2,3,4) dimana
letak kedua titik tersebut
Penyelesaian 4.1 :
. Titik P(2,1,2) , maka artinya titik P terletak pada 2 satuan dari
Sumbu  X , 1 satuan dari Sumbu  Y dan 2 satuan dari
Sumbu  Z artinya titik P terletak pada Oktan pertama
. Titik Q(2,3,4) , maka artinya titik Q terletak pada -2 satuan
Sumbu  X , -3 satuan dari Sumbu  Y dan 4 satuan dari
Sumbu  Z artinya titik Q terletak pada Oktan ketiga
dari
Geometri dalam Ruang, Vektor
131
Jika titik P( x, y, z ) sebenarnya merupakan jarak dari tiga bidang
tersebut, titik P( x, y, z ) berarti berjarak x dari bidang yz, berjarak y
dari xz dan berjarak z dari bidang xy sehingga jika digambar dalam
sistem koordinat dimensi tiga seperti Gambar 4.3.
Z
x
 (x,y,z)
O
z
X
Y
y
Gambar 4.3. Jarak ke tiga bidang
Contoh 4.2 :
Diketahui titik P(4,3,5) gambarkan dalam sistem koordinat dimesi
tiga
Penyelesaian 4.2 :
Gambar titik P(4,3,5) seperti bangun sebuah balok
Z
-4
O
3
X
Y
 (-4,3,-5)
-5
Geometri dalam Ruang, Vektor
132
4.1.1. Jarak Dua Titik
P1 x1 , y1 , z1  dan P2 x2 , y 2 , z 2  dalam
ruang dimensi tiga dimana x1  x2 , y1  y 2 dan z1  z 2 , P1 dan P2
Misalnya ada dua titik yaitu
merupakan titik sudut yang berlawanan didalam suatu balok seperti
pada Gambar 4.4.
Z
P2  x 2 , y 2 , z 2  
 P1 x1 , y1 , z1 
Y
Q
X
R
Gambar 4.4. Jarak Dua Titik
Jika kita letakan sebuah titik Q dan titik R ternyata masing-masing
Qx2 , y 2 , z1  dan titik R mempunyai
koordinat Rx2 , y1, z1 , karena segiriga P2 QP1 siku-siku di Q dan
titik mempunyai koordinat
QRP1 siku-siku di R , maka akan diperoleh panjang garis
P1 P2 dan panjang garis QP1 menurut rumus Pytagoras yaitu
segitiga
. P1 P2
2
 P2 Q  QP1
2
2
Dan
. QP1
2
 P1 P2
2
 P1 P2
2
 P1P2
2

 QR  RP1
2
2
sehingga panjang garis
 P2 Q  QR  RP1
2
2
2
 z 2  z1    y 2  y1   x2  x1 
2
2
2
atau
 x2  x1    y2  y1   z2  z1 
P1 P2 
2
2
2
x2  x1 2   y2  y1 2  z 2  z1 2
Geometri dalam Ruang, Vektor
133
P1 x1 , y1 , z1  dan P2 x2 , y 2 , z 2 
maka panjang atau jarak antara titik P1 dan P2 dirumuskan sebagai
Secara umum jika diketahui dua titik
berikut :
P1 P2 
x2  x1 2   y2  y1 2  z2  z1 2
Contoh 4.3 :
P3,4,2 dan Q 4,2,5 tentukan jarak titik P ke
titik Q atau PQ
Diketahui titik
Penyelesaian 4.3 :
Diketahui
adalah :
P3,4,2 dan Q 4,2,5 , maka jarak kedua titik itu

PQ 
x2  x1 2   y2  y1 2  z 2  z1 2

PQ 
 4  32   2  42  5  (2)2

PQ 
 72   62  72
 PQ
 42  36  42
 PQ
 120
 PQ
 10,95
Contoh 4.4 :
P4,5,3 dan Q 2,1,7 tentukan jarak titik P
ke titik Q atau PQ
Diketahui titik
Geometri dalam Ruang, Vektor
134
Penyelesaian 4.4 :
Diketahui titik P
titik itu adalah :
4,5,3
dan titik
Q 2,1,7 , maka jarak kedua

PQ 
x2  x1 2   y2  y1 2  z 2  z1 2

PQ 
 2  42   1   52   7  (3)2

PQ 
 62  42   42
 PQ
 36  14  14
 PQ
 64
 PQ
8
4.1.2. Bola dan Persamaanya
Pada pembahasan materi sebelumnya, yaitu telah diketahui bahwa
jarak dua buah titik misalnya titik P1 x1 , y1 , z1
dan titik
P2 x2 , y 2 , z 2 
adalah
P1 P2 
karena sebuah bola merupakan


x2  x1 2   y2  y1 2  z 2  z1 2 ,
himpunan titik P x, y, z  yang
berjarak sama atau konstan yaitu R atau jari-jari dari suatu titik
tetap Q a, b, c sebagai titik pusat bola, maka jarak setiap titik

P x, y, z 
adalah

ke titik pusat
PQ 
titik Q atau
Qa, b, c  menurut rumus jarak dua titik
x  a 2   y  b2  z  c 2 ,
karena jarak titik P ke
PQ sama dengan jari-jari sebuah bola , maka PQ  R
x  a 2   y  b2  z  c 2 , maka
2
2
2
2
PQ  x  a    y  b  z  c  karena PQ  R , maka didapat
2
2
2
2
PQ  R 2 , sehingga diperoleh R 2  x  a    y  b  z  c 
dan karena
PQ 
maka persamaan bola dapat dirumuskan sebagai berikut :
x  a 2   y  b 2  z  c 2  R 2
Geometri dalam Ruang, Vektor
135
Jika kita gambarkan sebuah bola dengan titik pusat
a, b, c 
dengan
jari-jari R seperti pada Gambar 4.5.
Z
 x, y , z 

R

a, b, c 
Y
X
Gambar 4.5. Bola dengan titik pusat (a,b,c)
Jika persamaan x  a    y  b   z  c   R kita uraikan, maka
akan menjadi persamaan :
2
2
2
2
x  a 2   y  b2  z  c2  R 2
x 2  2ax  a 2  y 2  2by  b 2  z 2  2cz  c 2  R 2
2
2
2
2
2
2
2
 x  y  z  2ax  2by  2cz  a  b  c  R
2
2
2
2
2
2
2
 x  y  z  2ax  2by  2cz  a  b  c  R  0
2
2
2
2
Jika A  2a , B  2b , C  2c dan D  a  b  c  R , maka

persamaan akan menjadi :

x 2  y 2  z 2  Ax  By  Cz  D  0
Sehingga persamaan bola dengan titik pusat di
a, b, c  dengan jari-
jari R adalah :
x 2  y 2  z 2  Ax  By  Cz  D  0
Dengan Catatan :
A  2a
B  2b
C  2c
D  a2  b2  c2  R2
Geometri dalam Ruang, Vektor
136
Contoh 4.5 :
Tentukan persamaan bola yang berpusat di titik
jari 4.
2,4,2 dengan jari-
Penyelesaian 4.5 :
Diketahui titik
persamaanya :
pusat
2,4,2
bola
 x  a    y  b   z  c   R
2
2
2
jari-jarinya
R  4 , maka
2
  x  2   y  4   z  2  4
Sehingga persamaan bolanya adalah :
2
2
2
2
x  22   y  42  z  22
 16
Contoh 4.6 :
Tentukan persamaan bola yang berpusat di titik
jari 3.
0,0,0 dengan jari-
Penyelesaian 4.6 :
Diketahui titik
persamaanya :
pusat
bola
0,0,0
 x  a    y  b   z  c   R
2
2
2
2
2
R  3 , maka
2
  x  0   y  0   z  0  3
2
jari-jarinya
2
Sehingga persamaan bolanya adalah :
x2  y2  z 2  9
Contoh 4.7 :
Diketahui bola x
dan kari-jarinya
2
 y 2  z 2  10 x  8 y  12 z  68  0 , tentukan pusat
Geometri dalam Ruang, Vektor
137
Penyelesaian 4.7 :
x 2  y 2  z 2  10 x  8 y  12 z  68  0 ,
maka diperoleh data A  10 , B  8 , C  12 dan D  68 , karena
. A  2a
  2a  10
 a5
. B  2b
  2b  8
 b4
. C  2c
  2c  12
 c6
2
2
2
2
2
2
2
2
. D  a  b  c  R
 68  5  4  6  R
2
 R  25  16  36  68
2
 R 9
 R3
Diketahui persamaan bola
Sehingga diperoleh kesimpulan bola tersebut mempunyai titik pusat
di titik 5,4,6 dengan jari-jari R  3


Grafiknya seperti Gambar 4.6
Z
3

5,4,6
4
Y
5
X
Gambar 4.6. Bola dengan pusat (5,4,6) dan R=3
4.1.3. Titik Tengah
Hal lain yang berkaitan dengan jarak antara dua titik adalah titik
tengah, misalkan diketahui dua titik P1 x1 , y1 , z1 dan P2 x2 , y 2 , z 2
yang masing-masing merupakan titik ujung dari sebuah garis, jika
titik tengah dari garis tersebut dituliskan sebagai M m1 , m2 , m3 

dimana



m1 , m2 dan m3 diperoleh dari rumus :
y  y2
x  x2
z  z2
m2  1
m1  1
m3  1
2 ,
2 ,
2 .
Geometri dalam Ruang, Vektor
138
Jika kita gambar, maka seperti Gambar 4.7
Z
y1
m2
x2
m1
x1
X
z1
Y
z2
m3


y2

P2 x2 , y2 , z2 
M m1 , m2 , m3 
P1 x1 , y1 , z1 
Gambar 4.7. Titik tengah pada suatu Garis
Contoh 4.8 :
Tentukan titik tengah antara titik
P1 2,4,2 dan titi P2 6,4,8
Penyelesaian 4.8 :
P1 2,4,2 dan titik P2 6,4,8 maka koordinattitik
tengahnya adalah M m1 , m2 , m3  dimana :
x  x2
26 8
. m1  1
 m1 
 4
2
2
2
y  y2
4   4 0
. m 2  1
 m2 
 0
2
2
2
z  z2
 2   8  10
. m3  1
 m3 

 5
2
2
2
Sehingga titik tengah mempunyai koordinat M 4,0,5 , jika
Diketahui titik
kitagambarkan seperti pada Gambar 4.8
Geometri dalam Ruang, Vektor
139
Z
-4
4
2
X
6
Y
-5


2,4,2
M 4,0,5

6,4,8
Gambar 4.8. Titik tengah pada suatu Garis
Contoh 4.9 :
Tentukan persamaan bola yang pusatnya merupakan titik tengah
dari suatu garis yang dibentuk dari dua titik P1  1,2,3 dan titik

P2 5,2,7

Penyelesaian 4.9 :
Persoalan yang kita hadapi adalah pusat bola belum diketahui, jarijari belum diketahui, maka langkah pertama adalah menentukan
pusat bola dan jari-jari.
. Koordinat Titik tengah antara titik P1  1,2,3 dan titik P2 5,2,7
adalah
M m1 , m2 , m3  dimana :
x1  x 2
2
y  y2
m2  1
2
z  z2
m3  1
2




1 5 4
 2
2
2
2   2 0
 m2 
 0
2
2
3  7 10
 m3 

5
2
2
Jadi titik tengahnya M 2,0,5 dan titik tengah ini merupakan
m1 
 m1 
titik pusat bola
Geometri dalam Ruang, Vektor
140
. Jari-jari bola adalah jarak titik tengah M 2,0,5 ke titik
P1  1,2,3 yaitu
atau jarak titik
P1 M
M 2,0,5 ke titik
P2 5,2,7 yaitu P2 M

P1 M 
m1  x1 2  m2  y1 2  m3  z1 2

P1 M 
2   12  0  22  5  32

P1 M 
32   22  22

P1 M  9  4  4

P1 M  17
Sehingga persamaan bola yang dimaksud adalah :
 x  2   y  0  z  5 
2
2
2
 x  2  y  z  5  17
Atau dalam bentuk :
2
 17 
2
2
2
x 2  y 2  z 2  4 x  10 z  12  0
4.1.4. Persamaan Bidang Datar
Grafik dalam ruang dimensi tiga pada prinsipnya sama dengan grafik
pada bidang dimensi dua, jika pada dimensi dua berupa garis, maka
pada dimensi tiga akan berupa bidang, demikian juga jika pada
dimensi dua berupa bidang, maka jika digambar pada dimensi tiga
akan berupa ruang.
Persamaan linier pada ruang dimensi tiga merupakan sebuah bidang,
secara umum persamaan linier dalam ruang dimensi tiga dirumuskan
sebagai berikut :
Ax  By  Cz  D
dengan syarat A  B  C  0
jika suatu bidang S memotong ke tiga sumbu koordinat yaitu
sumbu-x, sumbu-y dan sumbu-z, maka untuk menggambar grafiknya
kita tentukan titik potong pada ketiga sumbu tersebut, yaitu titik
potong sumbu-x yaitu P x,0,0 , titik potong sumbu-y yaitu Q 0, y,0
2
2
2

Geometri dalam Ruang, Vektor



141


dan titik potong sumbu-z yaitu R 0,0, z , untuk menentukan nilai
x, y dan z sebagai berikut :
. Untuk menentukan nilai x , maka kita beri nilai y  0 dan z  0
x  0 dan z  0
. Untuk menentukan nilai z , maka kita beri nilai x  0 dan y  0
Sehingga akan diperoleh ketiga titik potong yaitu Px,0,0 , Q0, y,0
dan R0,0, z 
. Untuk menentukan nilai y , maka kita beri nilai
Contoh 4.10 :
Gambarkan grafik dari persamaan 3x  4 y  2 z  12
Penyelesaian 4.10 :
Untuk menentukan ke tiga titik potong terhadap sumbu-sumbu
koordinat, maka kita tentukan nilai-nilai x, y dan z , yaitu :
x , maka kita beri nilai y  0 dan z  0
dan kita substitusikan ke persamaan 3x  4 y  2 z  12 , maka
. Untuk menentukan nilai
diperoleh
 3x  4(0)  2(0)  12
 3x  0  0  12
 3x  12
x  4 sehingga titik potong sumbu-x adalah P4,0,0
. Untuk menentukan nilai y , maka kita beri nilai x  0 dan z  0
dan kita substitusikan ke persamaan 3x  4 y  2 z  12 , maka

diperoleh
 3(0)  4 y  2(0)  12
 0  4 y  0  12
 4 y  12
Q0,3,0
. Untuk menentukan nilai z , maka kita beri nilai x  0 dan y  0
dan kitasubstitusikan ke persamaan 3x  4 y  2 z  12 , maka
 y  3 sehingga titik potong sumbu-y adalah
diperoleh
 3(0)  4(0)  2 z  12
 0  0  2z
 12
Geometri dalam Ruang, Vektor
142
 2 z  12
 z  6 sehingga titik potong sumbu-z adalah R 0,0,6
Sehingga kita peroleh titik-titik potong terhadap ke tiga sumbu yaitu
P 4,0,0 , Q 0,3,0 dan R 0,0,6 jika kita letakkan ketiga titik
tersebut pada sistem koordinat dimensi tiga, maka akan terlihat pada
Gambar 4.9






Z


 R0,0,6
3 x  4 y  2 z  12

X
Q0,3,0

Y
P4,0,0
Gambar 4.9. Bidang dari sebuah persamaan
Contoh 4.11 :
Gambarkan grafik dari persamaan 4 x  6 y  12
Penyelesaian 4.11 :
Karena persamaannya 4 x  6 y  12 dimana tidak mengandung
variable z , maka grafiknya sebuah bidang yang sejajar dengan
sumbu- z , artinya tidak memiliki titik potong terhadap sumbu- z ,
Untuk menentukan ke dua titik potong terhadap sumbu-sumbu
koordinat, maka kita tentukan nilai-nilai x dan y , yaitu :
x , maka kita beri nilai y  0 dan kita
substitusikan ke persamaan 4 x  6 y  12 , maka diperoleh
 4 x  6(0)  12
 4 x  0  12
 4 x  12
 x  3 sehingga titik potong sumbu-x adalah P3,0,0
. Untuk menentukan nilai
Geometri dalam Ruang, Vektor
143
x  0 dan kita
. Untuk menentukan nilai y , maka kita beri nilai
substitusikan ke persamaan 4 x  6 y  12 , maka diperoleh
 4 x  6 y  12
 4(0)  6 y  12
 6 y  12
 y  2 sehingga titik potong sumbu-y adalah
Q0,2,0
Karena dalam persamaan 4 x  6 y  12 tidak ada variabel z , maka
berarti bidang datar tersebut sejajar dengan sumbu-z, sehingga tidak
ada titik potong sumbu-z, kita hanya memperoleh titik potong
terhadap sumbu-x yaitu P 3,0,0 , dan titik potong sumbu-y yaitu




Q 0,2,0 jika kita letakkan kedua titik tersebut pada sistem koordinat
dimensi tiga, maka akan terlihat pada Gambar 4.10
Z
4 x  6 y  12

X
Q0,2,0
Y
 P3,0,0
Gambar 4.10. Bidang Sejajar Sumbu-z
Contoh 4.12 :
Gambarkan grafik dari persamaan
2x  4z  8
Penyelesaian 4.12 :
Karena persamaannya 2 x  4 z  8 dimana tidak mengandung
variable y , maka grafiknya sebuah bidang yang sejajar dengan
sumbu- y , artinya tidak memiliki titik potong terhadap sumbu- y ,
Geometri dalam Ruang, Vektor
144
Untuk menentukan ke dua titik potong terhadap sumbu-sumbu
koordinat, maka kita tentukan nilai-nilai x dan z , yaitu :
. Untuk menentukan nilai x , maka kita beri nilai z  0 dan kita
substitusikan ke persamaan 2 x  4 z  8 , maka diperoleh
 2 x  4(0)  8
2x  0  8
2x  8
 x  4 sehingga titik potong sumbu-x adalah P4,0,0
. Untuk menentukan nilai z , maka kita beri nilai x  0 dan kita
substitusikan ke persamaan 2 x  4 z  8 , maka diperoleh
 2x  4z  8
 2(0)  4 z  8
 4z  8
 z  2 sehingga titik potong sumbu-z adalah R0,0,2
Karena dalam persamaan 2 x  4 z  8 tidak ada variabel y , maka


berarti bidang datar tersebut sejajar dengan sumbu-y, sehingga tidak
ada titik potong sumbu-y, kita hanya memperoleh titik potong
terhadap sumbu-x yaitu P 4,0,0 , dan titik potong sumbu-z yaitu




R 0,0,2 jika kita letakkan kedua titik tersebut pada sistem koordinat
dimensi tiga, maka akan terlihat pada Gambar 4.11
Z

P4,0,0

Q0,0,2 2 x  4 z  8
Y
X
Gambar 4.11. Bidang Sejajar Sumbu Y
Geometri dalam Ruang, Vektor
145
4.1.5. Soal-Soal Latihan
P6,1,3 ke titik Q2,2,5
1. Tentukan jarak titik

 



2. Diketahui titik-titik 4,5,2 , 1,7,3 dan 2,4,5 merupakan titik
sudut suatu segitiga, perlihatkan bahwa segitiga tersebut adalah
segitiga sama sisi

 



3. Diketahui titik-titik 1,0,5 , 3,6,8 dan 7,4,7 merupakan titiktitik sudut suatu segitiga, perlihatkan bahwa segitiga tersebut
adalah segitiga siku-siku dengan bantuan teorema Phytagoras
4. Sebuah kotak persegipanjang sisi-sisinya sejajar bidang-bidang
koordinat dan sebagai titik ujung diagonal utamanya adalah 2,3,4




dan 5,2,0 , Gambarkan kotak itu dan cari koordinat ke delapan
titik sudutnya
5. Tuliskan persamaan bola yang titik pusatnya dan jari-jarinya
sebagai berikut :
a.
c.
3,1,4 , 5
 6,2,3 , 2
b.
d.
 1,0,4 ,
3,0,0 , 3
6. Cari persamaan bola yang pusatnya
bidang xy
6
2,4,5
dan menyinggung
7. Tentukan pusat bola dan jari-jarinya dari persamaan bola di
bawah ini
x 2  y 2  z 2  12 x  14 y  8z  1  0
2
2
2
b. x  y  z  2 x  6 y  10 z  34  0
2
2
2
c. 4 x  4 y  4 z  4 x  8 y  16 z  12  0
2
2
2
d. x  y  z  8x  4 y  22 z  77  0
a.
8. Buatkan sketsa grafik dari persamaan yang diketahui
a. 2 x  6 y  3z  12
b. 3x  4 y  2 z  24
d.  3x  2 y  z  6
c. x  3 y  z  6
9. Tentukan persamaan bola yang mempunyai ruas garis yang
menghubungkan titi  2,3,6 dan 4,1,5 sebagai garis tengah

Geometri dalam Ruang, Vektor



146