3. Sudut Khusus a. Sudut 0 0 ,3600 dan 1800 Perhatikan gambar
advertisement
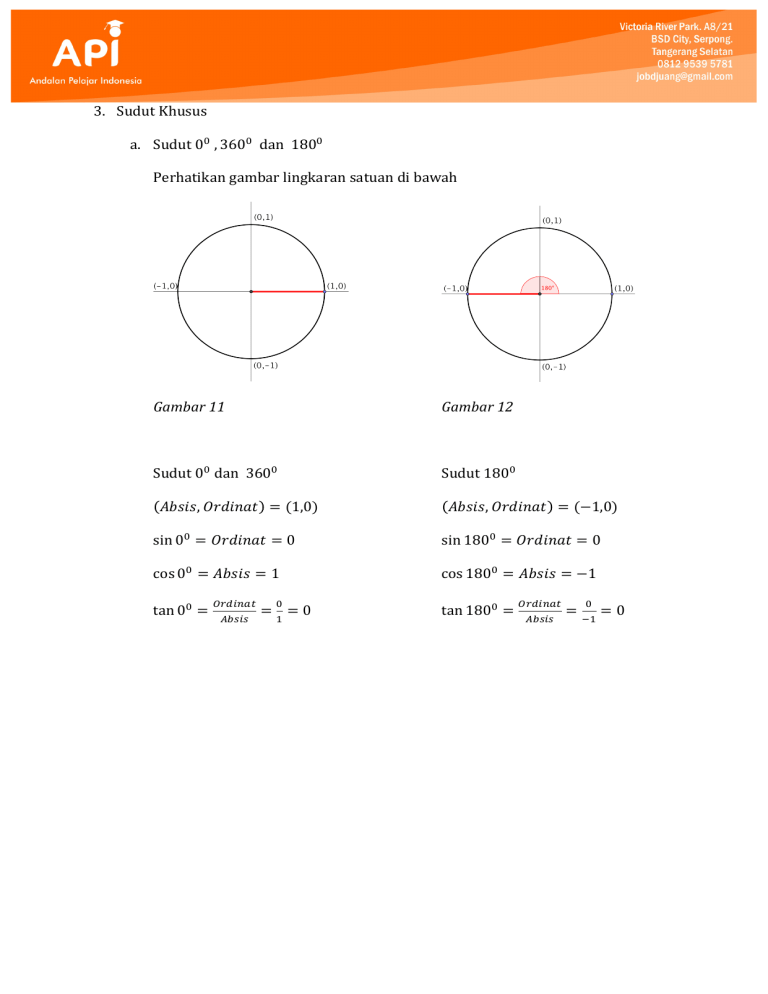
3. Sudut Khusus a. Sudut 0! , 360! dan 180! Perhatikan gambar lingkaran satuan di bawah Gambar 11 Sudut 0! dan 360! π΄ππ ππ , πππππππ‘ = (1,0) sin 0! = πππππππ‘ = 0 cos 0! = π΄ππ ππ = 1 !"#$%&' ! tan 0! = !"#$# = ! = 0 Gambar 12 Sudut 180! sin 180! = πππππππ‘ = 0 cos 180! = π΄ππ ππ = −1 tan 180! = π΄ππ ππ , πππππππ‘ = (−1,0) !"#$%&' !"#$# ! = !! = 0 b. Sudut 90! dan 270! Perhatikan gambar lingkaran satuan di bawah Gambar 13 Sudut 90! π΄ππ ππ , πππππππ‘ = (0,1) sin 90! = πππππππ‘ = 1 cos 90! = π΄ππ ππ = 0 !"#$%&' ! tan 90! = !"#$# = ! = ∞ Gambar 14 Sudut 270! sin 270! = πππππππ‘ = −1 cos 270! = π΄ππ ππ = 0 tan 270! = π΄ππ ππ , πππππππ‘ = (0, −1) !"#$%&' !"#$# = !! ! = −∞ c. Sudut 30! dan 60! βπ΄π΅πΆ adalah segitiga sama sisi dengan panjang sisi sisinya adalah π Pada segitiga sama sisi semua sudutnya adalah 60! π΄π adalah garis tinggi sekaligus garis bagi dan garis berat sehingga ∠π΅π΄π = ∠πΆπ΄π = !"! ! = 30! Lihat βπ΄ππ΅ siku siku di π π΄π΅! = π΄π ! + π΅π ! π! = π΄π ! + !! ! ! !! ! ! !! ! = π΄π ! + − !! ! ! π΅π = πΆπ = ! Gambar 15 ! ! ! !! ! = π΄π ! ! !! ! ± = π΄π ! dan ! ! ± 3 ! = π΄π = π΄π tan 30! ! sin 30 !" cos 30 = !" = sin 30! ! ! ! ! ! =! !" = !" = cos 30! = ! ! ! ! ! = = = ! ! tan 30 = = !" !" ! ! ! ! ! ! ! ! × ! ! ! ! ! Gambar 15 sin 60! !" = !" = sin 60! = ! ! ! ! ! ! cos 60! = cos 60! !" tan 60! = !" ! ! ! ! =! !" = !" = tan 60! ! ! ! ! ! = 3 d. Sudut 45! βπ΄π΅πΆ adalah segitiga siku siku sama kaki dengan panjang sisi miringnya adalah π dan π΄πΆ = π΅πΆ Lihat βπ΄πΆπ΅ siku siku di πΆ π΄π΅! = π΄πΆ ! + π΅πΆ ! ! π = π΄πΆ ! + π΄πΆ ! π! = 2π΄πΆ ! !! Gambar 16 = π΄πΆ ! ! !! ± ! ±π ! ±π ! ! ! = π΄πΆ ! = π΄πΆ = π΄πΆ ! ± ! 2 = π΄πΆ !" sin 45! = !" = sin 45! = ! ! ! ! ! ! cos 45! !" = !" = cos 45! = ! ! ! ! ! ! tan 45! !" = !" = !" !" tan 45! =1
![SDOF2 Respons Getaran Bebas [Compatibility Mode]](http://s1.studylibid.com/store/data/004299603_1-3cfa31a1cbb8989714a57a1dc7b26b0d-300x300.png)
