persamaan eksponen

Persamaan
Eksponen
fungsi eksponen adalah fungsi yang memetakan setiap
bilangan real x ke bilangan real ax
PERSAMAAN
EKSPONEN
persamaan eksponen adalah persamaan bentuk eksponen
yang memuat variabel
Pertidaksamaan eksponen:
- jika bilangan pokok a > 1, maka tanda ketidaksamaan tetap
- jika bilangan pokok 0 < a < 1, maka tanda ketidaksamaan berubah
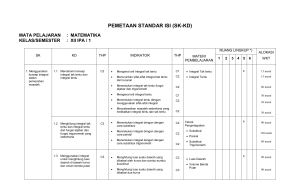
Standart Kompetensi
5. Menggunakan aturan yang berkaitan dengan fungsi eksponen dalam pemecahan
masalah.
Kompetensi Dasar
5.1. Menggunakan sifat-sifat fungsi eksponen dalam pemecahan masalah.
5.2. Menggambar grafik fungsi eksponen.
5.3. Menggunakan sifat-sifat fungsi eksponen dalam penyelesaian pertidaksamaan
eksponen sederhana
Indikator
1.
Mendefinisikan fungsi eksponen
2. Menyelesaikan masalah yang berkaitan dengan fungsi eksoponen
3. Menentukan nilai fungsi eksponen untuk menggambar grafik
4. Mendefinisikan persamaan eksponen
5. Menentukan penyelesaian persamaan eksponen
6. Menentukan penyelesaian pertidaksamaan eksponen dan syaratnya
35/ Matematika SMA (2)/MA Nurul Huda / By Triyanti Mandasari
Persamaan
Eksponen
PERSAMAAN EKSPONEN
 Fungsi Eksponen

Fungsi eksponen adalah fungsi yang memetakan setiap bilangan real x ke
bilangan real ax. Dengan a > 0 dan a ≠ 1.

Bentuk umum fungsi eksponen:
y = f(x) = kax atau f : x → kax
x = peubah bebas dengan daerah asal (domain) D = {𝑥|−∞ < 𝑥 <∝, 𝑥 𝜖 𝑅}
a = bilangan pokok (basis) dengan syarat a > 0 dan a ≠ 1 (0 < a < 1 atau a > 0)
y = peubah tak bebas
k = konstanta sembarang

Menggunakan fungsi eksponen untuk meyelesaikan soal yang berkaitan dengan
pertumbuhan dan peluruhan. Example: pertumbuhan penduduk di suatu kota,
bertambahnya uang tabungan di bank, penyusutan harga barang.
Jika tingkat suku bunga di bank sebesar p % per tahun, setelah t tahun uang
simpanan di bank menjadi:
𝑝
A(t) = A0 (1 + 100)
𝑡
Persamaan ini dapat dinyatakan sebagai fungsi eksponen f(x) = kax
k = konstanta positif dan a > 0.
Pada waktu dibeli, harga sebuah komputer sebesar P 0 dan harga tersebut dari
tahun ke tahun menyusut sebesar p % sehingga harga komputer pada akhir tahun
ke t sebesar:
𝑝
P(t) = P0 (1 − 100)
𝑡
Persamaan ini dapat dinyatakan sebagai fungsi eksponen f(x) = kax
k = konstanta positif dan 0 < a < 1.
Contoh Soal
1. Diketahui grafik fungsi eksponen seperti gambar di
samping!
Tentukan rumus fungsi grafik tersebut!
a. y = 2x
1 𝑥
b. y = (2)
d. y = x2
1
e. y = 2𝑥
c. y = 2x
36/ Matematika SMA (2)/MA Nurul Huda / By Triyanti Mandasari
Persamaan
Eksponen
2. Pak Andi memiliki tabungan sebesar Rp 5.000.000,00 di sebuah bank yang
memberikan bunga majemuk 1,5 % per bulan. Berapa besar uang tabungan Pak
Andi setelah 3 bulan?
(Rp. 5.228.392,00)
Kaji Soal
1. Diketahui grafik fungsi eksponen seperti gambar di
samping!
Tentukan rumus fungsi grafik tersebut!
33
1 𝑥
a. y = 2 √(2)
1 𝑥
3
1 𝑥
23
1 𝑥
e. y = 3 √(2)
b. y = (2)
1
c. y = √(2)
12
d. y = 2 √(2)
𝑥
2. Diketahui grafik fungsi eksponen seperti gambar di
samping!
Persamaan grafik fungsi eksponen tersebut adalah!
a. y = 3x
1 𝑥
b. y = (3)
d. y = x3
1
e. y = 3𝑥
c. y = 3x
 Persamaan Eksponen
Persamaan eksponen adalah persamaan bentuk eksponen yang memuat variabel.
Beberapa bentuk persamaan eksponen beserta penyelesaiannya:

af(x) = am dengan a > 0 dan a ≠ 1.
Penyelesaiannya ditentukan dengan menyelesaikan f(x) = m

af(x) = ag(x) dengan a > 0 dan a ≠ 1.
Penyelesaiannya ditentukan dengan menyelesaikan f(x) = g(x)

af(x) = bf(x) dengan a > 0, a ≠ 1, b > 0, b ≠ 1, dan a ≠ b
Penyelesaiannya ditentukan dengan menyelesaikan f(x) = 0

(h(x))f(x) = (h(x))g(x)
Penyelesaiannya ditentukan dengan menyelesaikan:
-
f(x) = g(x)
-
h(x) = 1
-
h(x) = 0 dengan syarat f(x) dan g(x) keduanya positif
-
h(x) = –1 dengan syarat f(x) dan g(x) keduanya genap atau keduanya ganjil
37/ Matematika SMA (2)/MA Nurul Huda / By Triyanti Mandasari
Persamaan

Eksponen
A(af(x))2 + B(af(x)) + C dengan a > 0, a ≠ 1, A ≠ 1, dan A, B, C 𝜖 R
Penyelesaiannya dicari dengan memisalkan p = af(x) sehingga diperoleh
persamaan kuadrat dalam p.
Contoh Soal
1. Tentukan himpunan penyelesaian dari persamaan berikut:
a. 3𝑥
2 +3𝑥+4
b. 3𝑥
2 −5𝑥+4
HP(-3, -2)
= 9−𝑥−1
= 5𝑥
HP(1, 4)
2 −5𝑥+4
c. (2𝑥 − 3)𝑥+1 = (2𝑥 − 3)𝑥
HP(-2,
2 +𝑥−3
𝟑
𝟐
, 2)
2. Akar – akar persamaan 32 + x + 31 – x = 12 adalah x1 dan x2. Jika x1 > x2, tentukan
x1 = 0 dan x2 = -1
nilai x1 dan x2?
Kaji Soal
1. Penyelesaian persamaan 3𝑥
2 +𝑥−2
= 81𝑥+2 adalah a dan b. Jika a > b, nilai a – b =
.....
a. 9
c. 5
b. 7
d. 3
e. 1
2. Himpunan penyelesaian persamaan (𝑥 − 2)𝑥+3 = (𝑥 − 2)2𝑥−1 adalah....
a. {4, 3}
c. {4, 3, 1}
b. {4, 3, 2}
d. {4, 3, 2, 1}
e. {4, 3, 2, 1, 0}
1
3. Tentukan himpunan penyelesaian persamaan 92𝑥−4 = (27)
𝑥 2 −4
 Pertidaksamaan Eksponen
Tetap atau berubahnya tanda ketidaksamaan tergantung dari nilai bilangan pokoknya.
Untuk a > 1 (tanda ketidaksamaan tetap)
Jika af(x) > ag(x) maka f(x) > g(x)
Jika af(x) ≥ ag(x) maka f(x) ≥ g(x)
Jika af(x) < ag(x) maka f(x) < g(x)
Jika af(x) ≤ ag(x) maka f(x) ≤ g(x)
Terlihat pada pertidaksamaan eksponen jika bilangan pokok a > 1, maka tanda
ketidaksamaan tetap.
38/ Matematika SMA (2)/MA Nurul Huda / By Triyanti Mandasari
Persamaan
Eksponen
Untuk 0 < a < 1 (tanda ketidaksamaan berubah)
Jika af(x) > ag(x) maka f(x) < g(x)
Jika af(x) ≥ ag(x) maka f(x) ≤ g(x)
Jika af(x) < ag(x) maka f(x) > g(x)
Jika af(x) ≤ ag(x) maka f(x) ≥ g(x)
Terlihat pada pertidaksamaan eksponen jika bilangan pokok 0 < a < 1, maka tanda
ketidaksamaan berubah.
Contoh Soal
1. Tentukan himpunan penyelesaian pertidaksamaan berikut:
2
1 𝑥 −3𝑥−5
a. (3)
1 −𝑥−2
𝟏
< (3)
{𝐱|𝐱 > 𝟐}
1 −𝑥+2
b. 83𝑥−4 > (32)
{𝐱|𝐱 < −1} atau 𝐱 > 3
2. Tentukan himpunan penyelesaian pertidaksamaan 4𝑥+1 − 3. 2𝑥+1 + 2 ≤ 0!
{𝐱|−𝟏 ≤ 𝐱 ≤ 𝟎}
Kaji Soal
1
1. Himpunan penyelesaian dari pertidaksamaan
4
a. {𝑥|− 3 ≤ 𝑥 ≤ 1}
1 2𝑥−4
(9)
2
≤ 274−𝑥 adalah...
1
d. {𝑥|−4 ≤ 𝑥 ≤ 3}
4
e. {𝑥|−4 ≤ 𝑥 ≤ 1}
b. {𝑥|−1 ≤ 𝑥 ≤ 3}
1
c. {𝑥|− 3 ≤ 𝑥 ≤ 4}
2. Nilai x yang memenuhi pertidaksamaan 32𝑥 − 4. 3𝑥+1 > 27 adalah....
a. 1 < x < 2
c. x < 1 atau x > 2
b. 2 < x < 9
d. x < 1 atau x > 3
e. x < 3 atau x > 9
 Kaji Soal UN
1. Nilai x yang memenuhi pertidaksamaan 32𝑥+1 + 8. 3𝑥 − 3 > 0 adalah... (UN 2011)
1
a. x < 3
c. x > 3
b. x > 3
d. x > –1
e. x < –3
2. Nilai x yang memenuhi pertidaksamaan 32𝑥+1 + 9 − 28. 3𝑥 > 0 adalah... (UN 2011)
a. x > –1 atau x > 2
d. x < –1 atau x > 2
b. x < –1 atau x < 2
e. x > –1 atau x < –2
c. x < 1 atau x > 2
39/ Matematika SMA (2)/MA Nurul Huda / By Triyanti Mandasari