MATEMATIKA DISKRIT - Staffsite STIMATA

MATEMATIKA DISKRIT
MATEMATIKA DISKRIT
MATEMATIKA DISKRIT
BAB I
HIMPUNAN
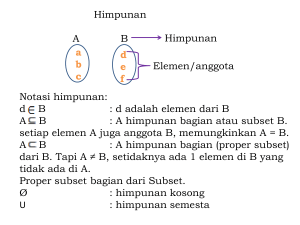
Huruf-huruf besar A, B, C, ... menyatakan himpunan dan huruf-huruf kecil a, b, c, ...
menyatakan elemen-elemen atau anggota dari himpunan.
Notasi himpunan :
pЄA
p adalah elemen dari A atau p anggota dari A
A⊆ B atau B ⊇ A
A adalah himpunan bagian/samadengan (subset) B atau
B mengandung A
A ⊂ B atau B⊃A
A adalah himpunan bagian (proper subset) dari B atau
sebaliknya;
∅
himpunan kosong
∪/S
himpunan semesta
1. Himpunan
a. Suatu himpunan ditunjukkan oleh anggota-anggota himpunannya (Prinsiple of
Extension) : Dua himpunan A dan B adalah sama jika dan hanya jika mereka
mempunyai anggota yang sama.
b. Suatu himpunan dapat digambarkan dalam hal sifatnya (Prinsiple of
Abstraction) : Diberikan sembarang himpunan U dan mempunyai sifat
himpunan P, ada suatu himpunan A sedemikian hingga elemen-elemen dari A
merupakan anggota dari himpunan U yang mempunyai sifat himpunan P.
c. Himpunan Ø tidak memuat satu elemenpun. Himpunan {0} memuat satu
elemen yaitu 0. Himpunan {Ø} juga memuat satu elemen yaitu himpunan
kosong (ini adalah himpunan dari himpunan).
d. A ⊆ B (A adalah subset dari B) menyatakan bahwa setiap elemen dari A juga
anggota dari B, yang memungkinkan bahwa A = B.
A ⊂ B (A adalah proper subset dari B) menyatakan bahwa A adalah himpuan
bagian dari B tetapi A ≠ B; atau setidaknya satu elemen di B yang tidak ada
di A
e. (ii)
(i) Untuk
Untuk sembarang
sembarang himpunan
himpunan A,
A, kita
kita mempunyai
mempunyai ØA ⊆
⊆ AA ⊆ U
(iii) Jika A ⊆ B dan B ⊆ C, maka A ⊆ C
(iv) A = B jika dan hanya jika A ⊆ B dan B ⊆ A
Bukti :
MATEMATIKA DISKRIT
(i)
(ii)
(iii)
(iv)
Setiap himpunan A adalah suatu subset dari himpunan U karena,
menurut definisi, semua anggota dari A adalah anggota dari U. Demikian
juga himpunan Ø adalah subset dari A
Setiap himpunan A adalah subset dari dirinya sendiri karena elemen
elemen dari A adalah anggota dari A.
Jika setiap elemen dari himpunan A anggota dari B, dan setiap elemen
dari B adalah anggta dari suatu himpunan C, maka jelas setiap elemen
dari
makaAAadalah
⊆ C. anggota dari C. dengan kata lain, jika A ⊆ B dan B ⊆ C,
Jika A ⊆ B dan B ⊆ C maka A dan B mempunyai elemen-elemen yang
sama, sehingga A = B. sebaliknya jika A = B maka A ⊆ B dan B ⊆ C
karena setiaphimpunan adalah subset dari dirinya sendiri.
Contoh :
1. Tulislah kembali pernyataan-pernyataan berikut dengan menggunakan notasi
himpunan :
a. 1 bukan anggota dari himpunan A → 1∉ A
b. 5 adalah anggota dari himpunan B → 5 ∈ B
c. A adalah himpunan bagian/sama dengan (subset) C → A ⊆ C
d. A bukan himpunan bagian/sama dengan (subset) D → A⊈ D
e. F mengandung semua elemen dari G → G ⊆ F atau F ⊇ G
f. E dan F mengandung elemen-elemen yang sama → E = F
2. Tuliskan elemen dari himpunan-himpunan berikut; dalam hal ini N = {1, 2,
3,…}
a. A = {x : x ∈ N, 3 ˂ x ˂12} → A = {4, 5, 6, 7, 8, 9, 10, 11}
b. B ={x : x ∈ N, x bilangan genap, x ˂ 15} → B = {2, 4, 6, 8, 10, 12, 14}
c. C = {x : x ∈ N, 4 + x = 3} → C = Ø
Latihan Soal :
1. Tuliskan elemen-elemen dari himpunan berikut; dalam hal ini N = {1, 2, 3, …)
a. A = {x : x Є N, 3 ˂ x < 9}
b. B = {x : x Є N, x2 + 1 = 10}
c. C = {x : x Є N, x bilangan ganjil, -5 < x < 5}
2. Tuliskan elemen-elemen dari himpunan berikut; dalam hal ini Z = {bilangan
bulat)
a. A = {x : x Є Z, 3 ˂ x < 9}
b. B = {x : x Є Z, x2 + 1 = 10}
c. C = {x : x Є Z, x bilangan ganjil, -5 < x < 5}
MATEMATIKA DISKRIT
3. Tentukan himpunan-himpunan berikut dengan menuliskan elemen-elemennya
a. A = {x : x Є R, -5 ˂ x < 5}
b. B = {x : x Є N, x kelipatan 3}
c. C = {x : x warga negara Indonesia, x adalah remaja}
4. Misalkan A = {x : 3x = 6}. Apakah A = 2?
5. Perhatikan himpunan-himpunan berikut : {w}, {y, w, z}, {w, y, x}, {y, z, w},
{w, x, y, z}, {z, w}. Manakah dari himpunan-himpunan tersebut yang sama
dengan himpunan A = {w, y, z}?
2. Diagram Venn
a.
b.
Himpunan A dan AB dan
dapat
diperbandingkan
(comparable
) jika A ⊆ B atau)
B⊆A;
B tidak
dapat diperbandingkan
(noncomparable
jika A sedangkan
⊈ B dan B ⊈ A.
Himpunan A dan B adalah disjoint jika mereka tidak mempunyai elemen
yang sama, yaitu bila tidak ada elemen di A yang menjadi anggota di B dan
tidak ada elemen di B yang menjadi anggota di A.
Sebuah diagram Venn adalah suatu perwakilan gambar dari himpunan-himpunan
berupa titik-titik dalam bidang. Himpunan semesta U diwakili oleh bagian dalam
suatu persegi, dan himpunan-himpunan yang lain diwakili oleh cakram-cakram
dalam persgi. Jika A ⊆ B, maka perwakilan cakram A seluruhnya akan berada di
dalam cakram B seperti gambar (a). jika A dan B disjoint,yaitu tidak mempuyai
elemen bersama. maka perwakilan cakram A akan terpisah dari cakram B seperti
gambar (b). Gambar (c) adalah beberapa objek ada di A tetapi tidak di B, ada di
B tetapi tidak di A, ada di A dan B, dan tidak di kedua-duanya.
(a) A ⊆ B
(b) A & B saling asing
(c)
U
B
A
A
U
Latihan soal :
1. Gambarkan sebuah diagram venn dari himpunan A, B dan C dimana A dan B
mempunyai elemen bersama, B dan C mempunyai elemen bersama, tetapi
himpunan A dan C disjoint.
2. Gambarkan sebuah diagram venn dari himpunan A, B dan C dimana A ⊆ B,
himpunan A dan C saling asing, tetapi himpunan B dan C mempunyai elemen
bersama
MATEMATIKA DISKRIT
3. Gambarkan sebuah diagram venn dari himpunan A, B dan C dimana ketiga
himpunan tersebut saling asing.
4. Gambarkan sebuah diagram venn dari himpunan A, B dan C dimana akan
membagi himpunan semesta U kedalam 23 = 8 bagian. Mengapa terdapat 8?
3. Operasi antar Himpunan
a. Gabungan (union)
Gabungan dari dua himpunan A dan B , dinyatakan dengan A U B, adalah
himpunan semua elemen A atau B :
A U B = {x : x Є A atau x Є B}
b. Irisan (intersection)
Irisan dua buah himpunan A dan B, dinyatakan dengan A ∩ B, adalah
himpunan yang elemen-elemennya merupakan anggota dari A dan juga B.
A ∩ B = {x : x Є A atau x Є B}
c. Komplemen suatu Himpunan (Absolute Complement)
Komplemen himpunan dinyatakan dengan Ac, adalah himpunan dari elemenelemen yang merupakan anggota semesta tetapi bukan anggota A :
Ac = {x : x Є U, x∉ A}
d. Selisih dari Dua Himpunan (The Relative Complement)
Selisih dari A dan B dinyatakan dengan A\B, adalah himpunan dari elemenelemen yang merupakan anggota dari A tetapi bukan anggota dari B :
A\B = {x : x Є A, x ∉ B}
AA
AUB
B
A
A∩B
B
A
A
Ac
B
A\B
Latihan soal :
Diketahui : U = {1, 2, 3, ..., 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8}, C ={3, 4, 5,
6}
Tentukan :
1) A U B
14) Bc
2) A U C
15) Cc
3) B U C
16) A\B
4) B U B
17) C\A
5) (A U B) U C
18) B\C
6) A U (B U C)
19) B\A
7) A ∩ B
20) B\B
MATEMATIKA DISKRIT
8) A ∩ C
9) B ∩ C
10)B ∩ B
11)(A ∩ B) ∩ C
12)A ∩ (B ∩ C)
13)Ac
21)
22)
23)
24)
25)
26)
A ∩ (B U C)
(A ∩ B) U (A ∩ C)
(A U B)c
Ac ∩ Bc
(A ∩ B)\C
(A\B)c
4. Aljabar Himpunan
Hukum atau sifat dari aljabar himpunan
1a. A U A = A
2a. (A U B) U C = A U (B U C)
3a. A U B = B U A
4a. A U (B ∩ C) = (A U B) ∩ (A U C)
5a. A U Ø = A
6a. A U S = S
8a. A U Ac = S
9a. Sc = Ø
10a. (A U B)c = Ac ∩ Bc
Hukum Idempotent
1b. A ∩ A = A
Hukum Assosiatif
2b. (A ∩ B) ∩ C = A ∩ (B ∩ C)
Hukum Komutatif
3b. A ∩ B = B ∩ A
Hukum Distributif
4b. A ∩ (B U C)= (A∩B) U (A ∩ C)
Hukum Identitas
5b. A ∩ S = A
6b. A ∩ Ø = Ø
Hukum Involusi
7. (Ac)c = A
Hukum Komplemen
8b. A ∩ Ac = Ø
9b. Ø = S
Dalil de Morgan
10b. (A ∩ B)c = Ac U Bc
Contoh :
Gunakan hukum-hukum pada tabel diatas untuk membuktikan identitas berikut :
(S ∩ A) U (B ∩ A) = A
(S ∩ A) U (B ∩ A) = (A ∩ S) U (A ∩ B)
sifat komutatif 3b
= A ∩ (S U B)
sifat distributif 4b
= A ∩ (B U S)
sifat komutatif 3a
=A∩S
sifat identitas 6a
=A
sifat identitas 5b
Latihan soal :
Buktikan identitas-identitas berikut :
1. (B U C) ∩ A = (B ∩ A) U (C ∩ A)
2. (B ∩ C) U A = (B U A) ∩ (C U A)
3. (A U B) ∩ (A U Bc) = A
4. A U (A ∩ B) = A
5. (Bc ∩ U) ∩ (Ac U Ø) = (A U B)c
MATEMATIKA DISKRIT
5. Argumen dan Diagram Venn
Pada bagian ini diagram venn digunakan untuk menunjukkan kebenaran dari
suatu argumen.
Contoh :
1. Terjemahkan setiap pernyataan berikut dalam bentuk diagram venn :
a. Semua mahasiswa adalah malas
b. Beberapa mahasiswa adalah malas
c. Tidak ada mahasiswa yang malas
d. Tidak semua mahasiswa adalah malas
Jawab :
orang malas
Orang
malas
mahasiswa
(a)
mahasiswa
Orang
malas
(b) dan (d)
mahasiswa
(c)
(a) Himpunan mahasiswa tercakup dalam himpunan orang malas seperti
ditunjukkan gambar a
(b) Himpunan mahasiswa dan orang malas mempunyai suatu elemen bersama
seperti gambar b
(c) Himpunan mahasiswa dan orang malas adalah saling asing seperti gambar
c.
(d) Dalam hal ini himpunan mahasiwa tidk tercakup dalam himpunan orangorang malas. Ini enunjuk pada gambar b (dengan kemungkinan bahwa
irisan himpunannya kosong)
2. Tunjukkan bahwa argumen berikut adalah benar :
S1 : Panci adalah sesuatu yang saya punya, terbuat dari timah
S2 : Saya mendapatkan semua pemberian kamu yang sangat berguna
S3 : Tak satupun dari panci saya yang berguna
S : Pemberian kamu pada saya bukan terbuat dari timah
 Menurut S1 barang dari timah tercakup dalam himpunan panci dan
menurut S3 himpunan panci dan barang berguna adalah saling asing;
seperti digambarkan dalam diagram venn berikut :
Barang dr timah
panci
Barang yg berguna
MATEMATIKA DISKRIT

Menurut S2 himpunan “hadiah anda” adalah subset dari himpunan barang
berguna seperti gambar berikut :
Hadiah anda
Barang
Barang yg berguna
panci
Kesimpulannya dengan jelas cocok oleh diagram venn di atas karena
himpunan “hadiah anda” adalah disjoint dari himpunan barang yang tebal
Latihan soal :
1. Perhatikan asumsi-asumsi berikut :
S1 : Penyair adalah orang yang bahagia
S2 : Setiap dokter adalah orang kaya
S3 : Tak satupun orang yang bahagia adalah orang kaya
Tunjukkan kebenaran dari setiap kesimpulan berikut :
a. Tak ada penyair yang kaya
b. Dokter adalah orang yang bahagia
c. Tak ada satupun yang menjadi penyair dan dokter
2. Tunjukkan bahwa argumen berikut adalah tidak benar :
S1 : Semua mahasiswa adalah pemalas
S2 : Tak seorangpun yang kaya adalah seorang mahasiswa
S : Orang pemalas adalah tidak kaya
3. Tunjukkan bahwa argumen berikut benar
S1 : Tidak ada mahasiswa yang pemalas
S2 : John adalah seorang artis
S3 : Semua artis adalah pemalas
S : John bukan seorang mahasiswa
4. Tunjukkan bahwa arguman berikut adalah benar :
S1 : Semua pengacara adalah orang kaya
S2 : Penyair adalah orang temperamental
S3 : Audrey adalah seorang pengacara
S4 : Tidak ada orang temperamental adalah orang kaya
S : Audrey bukan seorang penyair
MATEMATIKA DISKRIT
6. Induksi Lengkap
Prinsip bentuk induksi matematika yang ekuivalen :
1. Bentuk I : Misalkan P adalah sebuah proporsisi yang didefinisikan pada
bilangan bulat positif N; P(n) bisa benar atau salah utuk setiap n dalam N.
anggap P mempunyai dua sifat berikut :
(i)
P(1) adalah benar
(ii)
P(n + 1) bernilai benar bilaman P(n) benar
Maka P berlaku untuk setiap bilangan bulat positif.
2. Bentuk II (induksi lengkap) : Misalkan P adalah sebuah proporsisi yang
didefinisikan pada bilangan bulat positif N, sedemikian hingga :
(i)
P(1) adalah benar
(ii)
P(n) bernilai benar bilaman P(k) benar untuk setiap 1 ≤ k ≤ n.
Maka P berlaku untuk setiap bilangan bulat positif.
Prinsip induksi matematika dimulai dengan n0 = 1 dan membuktikanbahwa P(n)
berlaku untuk setiap n ≥ 1. Atau dapat dimulai dengan sembarang n0 = m dan
membuktikan bahwa P(n) berlaku untuk setiap n ≥ m.
Contoh :
1. Misalkan P adalah proposisi bahwa jumlah n bilangan ganjil pertama adalah
n2, yaitu, P(n): 1 + 3 + 5 + … + (2n - 1) = n2 (bilangan ganjil ke-n adalah 2n
– 1, dan bilangan ganjil berikutnya adalah 2n + 1). Buktikan P berlaku untuk
setiap bilangan bulat positif n Є N.
Penyelesaian :
Karena 1 = 12, maka P(1) benar. Asumsikan P(n) benar. kita tambahkan 2n +
1 pada kedua sisi P(n), di dapat :
1 + 3 + + 5 + … + (2n - 1) + (2n + 1) = n2 + (2n + 1) = (n + 1)2
yang mana adalah P(n + 1). Sehingga P(n + 1) benar bilaman P(n) benar.
Menurut prinsip induksi matematika, P berlaku untuk setiap n
2. Buktikan proposisi P, jumlah n bilangan bulat positif pertama adalah ½ n(n +
1); yaitu
P(n) : 1 + 2 + 3 + … + n = ½ n (n + 1)
Penyelesaian :
Proposisi berlaku untuk n = 1 karena 1 = ½ (1) (1 + 1), sehingga P(1) benar.
Asumsikan P(n) benar, kita tambahkan n + 1 pada keua sisi P(n), didapat :
1 + 2 + 3 + … + n + (n + 1) = ½ n (n + 1) + (n + 1)
= ½ [(n (n + 1) + 2(n + 1)]
= ½ [(n + 1)(n + 2)]
MATEMATIKA DISKRIT
Yang mana adalah P(n + 1) benar blamana P(n) benar. Menurut prinsip
induksi, P berlaku untuk setiap n.
Latihan soal :
Buktikan proposisi berikut :
1. P(n) : 12 + 22 + … + n2 =
2. P(n) : 1 + 4 + 7 + … + (3n – 2) =