A himpunan bagian a

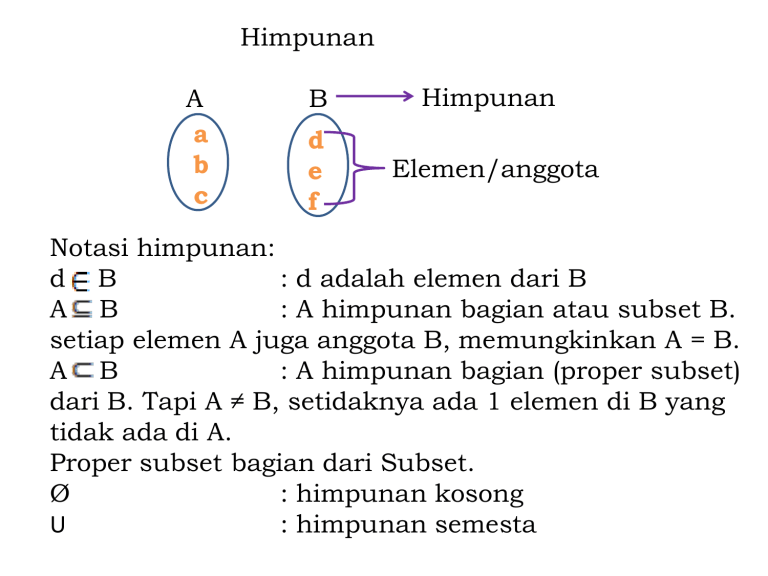
Himpunan
A
a
b
c
B
Himpunan
d
e
f
Elemen/anggota
Notasi himpunan:
d B
: d adalah elemen dari B
A B
: A himpunan bagian atau subset B.
setiap elemen A juga anggota B, memungkinkan A = B.
A B
: A himpunan bagian (proper subset)
dari B. Tapi A ≠ B, setidaknya ada 1 elemen di B yang
tidak ada di A.
Proper subset bagian dari Subset.
Ø
: himpunan kosong
U
: himpunan semesta
Ex:
Terangkan dengan kata-kata bagaimana
membuktikan setiap pernyataan berikut:
1. A sama dengan B.
2. A subset B.
3. A proper subset dari B.
4. A bukan subset dari B.
Teorema:
1. Untuk sembarang himpunan A, Ø ⊆ A ⊆ U.
2. Untuk sembarang himpunan A, A ⊆ A.
3. Jika A ⊆ B dan B ⊆ C, maka A ⊆ C.
4. A = B jika dan hanya jika A ⊆ B dan B ⊆ A.
anda
Soal:
1. Tunjukan bahwa A = [ a, b, c } bukan subset dari B =
{a, i, u, o, e}.
2. A = { a }, B = { a, c, b }, C = { c, a }, D = { c, b, a }, E = {
b }, Ø. Manakah dari himpunan tersebut yang
merupakan subset dari x = { a, b, c }? Dan manakah
yang merupakan proper subset dari X?.
3. A = { x, y, z }. Berapakah banyak subset dari A,
sebutkan?
4. Ø, A = { 1 }, B = { 1, 3 }, C = { 1, 5, 9 }, D = { 1, 2, 3, 4,
5 }, E = { 1, 3, 5, 7, 9 }, ⋃ = { 1, 2, 3, ... 8, 9 }.
I. Masukan simbol yang tepat a). Ø, A; b) A, B
II. Masukan simbol yang tepat a). B, C; b) B, E
III. Masukan simbol yang tepat a). C, D; b) C, E
IV. Masukan simbol yang tepat a). D, E; b) D, ⋃
N: himpunan bilangan positif: 1, 2, 3, …
Z: himpunan bilangan bulat: …-3, -2, -1, 0, 1, 2, 3…
Q: himpunan bilangan rasional
R: himpunan bilangan real
Himpunan dipisahkan tanda koma dan ditutup dengan { }.
Contoh:
A = { a, b, c, d} = himpunan A mempunyai elemen a, b, c,
d.
B = { x : x adalah bilangan bulat, x > 0 }.
B adalah himpunan dari x sedemikian hingga x
adalah bilangan bulat yang lebih besar dari 0.
Artinya:
 B mempunyai elemen bilangan bulat positif.
 x = tipe/jenis anggota himpunan.
 : = sedemikian hingga.
 , = dan.
Soal:
I. Tuliskan elemen – elemen dari himpunan berikut, N
= { 1, 2, 3, …}.
1. A = { x : x N, 3 < x < 12 }.
2. B = { x : x N, x bilangan genap, x < 15}.
3. C = { x : x N, 4 + x = 3 }.
II. Tuliskan elemen dari himpunan berikut:
1. A = { x : x N, 3 < x < 9 }.
2. B = { x : x N, X2 + 1 = 10 }.
3. C = { x : x N, x bilangan ganjil, -5 < x < 5 }.
III. Tuliskan elemen dari himpunan berikut, Z = {
bilangan bulat }
1. A = { x : x Z, 3 < x < 9 }.
2. B = { x : x Z, X2 + 1 = 10 }.
3. C = { x : x Z, x bilangan ganjil, -5 < x < 5 }.
Himpunan Kosong
{0} = memiliki 1 elemen yaitu 0
himpunan = tidak memuat 1 elemen pun
{ } = memuat 1 elemen yaitu himpunan kosong.
Contoh:
1. X = { x : X2 = 9, 2x = 4 }
2. Y = { x : x ≠ x}.
3. Z = { x : x + 8 = 8}.
Himpunan Semesta
= Anggota dari semua himpunan yang diamati
biasanya
merupakan
anggota
dari
suatu
himpunan besar tertentu.
Ex:
{ Dalam geometri } = { semua titik-titik dalam
bidang }.
Himpunan yang comparable, noncomparable,
saling
asing (disjoint)
 Himpunan A dan B dapat diperbandingkan
(comparable) jika A ⊆ B, atau B ⊆ A.
Himpunan A dan B tidak dapat diperbandingkan
(noncomparable) jika A⊈ B, atau B ⊈ A.
 himpunan A dan B disjoint jika A dan B tidak
memiliki elemen yang sama.
ex: diketahui:
A = { 1, 2 }, B = { 1, 2, 3, 4 }, C = { 1, 5 }, D = { 3, 4, 5 },
E = { 4, 5 }. Manakah dari himpunan tersebut yang
comparable? Noncomparable? Disjoint?
Operasi antar himpunan
a. Gabungan (union)
A U B = { x : x A atau x
a. Irisan (inter-section)
A B = { x : x A atau x
c.
Absolut complemen
himpunan).
Ac = { x : x U, x
A}
B}
B}
(komplemen
suatu
d. Relative complement (selisih dari A dan B).
A
={x:x
U, x
B}
Soal:
U = { 1, 2, 3, …, 8,9 }, A = { 1, 2, 3, 4 }, B = { 2, 4, 6, 8 },
C = { 3, 4, 5, 6 }.
Tentukan:
1. a). A U B, b). A U C, c). B U C, d). B U B.
2. a). (A U B) U C, b). A U (B U C).
3. a). A ∩ B, b). A ∩ C, c). B ∩ C, d). B ∩ B.
4. a). (A ∩ B) ∩ C, b). A ∩ (B ∩ C).
5. a). Ac, b). Bc, c). Cc .
6. a). A \ B, b). C \ A, c). B \ C, d). B \ A, e). B \ B.
7. a). A ∩ (B U C), b). ( A ∩ B ) U ( A ∩ C ).
8. a). (A U B)c , b). Ac Bc
9. a). ( A ∩ B ) \ C, b). ( A \ B )c