Matematika Ekonomi dan Bisnis

Matematika Ekonomi
FEUG
BUKU REFERENSI
1. Mathematical Analysis:
Business and Economic Applications, oleh Jean E. Weber,
Penerbit Harper & Row Inc., Cambrige.
2. Fundamental Methods of Mathematical Economics, oleh Alpha C. Chiang, McGraw-Hill
Publisher Inc., New York.
3. Matematika Untuk Ilmu Ekonomi dan Bisnis, oleh M. Nababan, Penerbit Erlangga, Jakarta.
4. Matematika Dasar Untuk Perguruan Tinggi, oleh Yusuf Yahya, Suryadi H.S, dan Agus S,
Penerbit Ghalia Indonesia, Jakarta.
5. Matematika Terapan Untuk Bisnis dan Ekonomi, oleh Dumairy, Penerbit BPFE Yogyakarta.
6. Pengantar Matematika Untuk Ekonomi, oleh H. Johannes dan Budiono Sri Handoko,
Penerbit LP3ES, Jakarta.
MATERI KULIAH
I.
Teori Himpunan
II.
Teori Bilangan
III.
Deret
IV.
Aplikasi Deret dalam Bisnis dan Ekonomi
V.
Fungsi Linear
VI.
Aplikasi Fungsi Linear dalam Bisnis dan Ekonomi
1. Fungsi Permintaan dan Fungsi Penawaran
2. Market Equilibrium
3. Pengaruh Pajak dan Subsidi terhadap Market Equilibrium
4. Fungsi biaya, Fungsi Penerimaan, dan Fungsi Profit
5. Analisis Break-Even
6. Fungsi pendapatan, Fungsi Konsumsi, dan Fungsi Tabungan
7. MPC dan MPS
VII.
Fungsi Non Linear
VIII. Aplikasi Fungsi Non Linear dalam Bisnis dan Ekonomi
IX.
Matriks dan Determinan
X.
Aplikasi Matriks dalam Bisnis dan Ekonomi
XI.
Sistem persamaan Linear.
©Rina Sugiarti
Page 1
Matematika Ekonomi
FEUG
TEORI HIMPUNAN (SET THEORY)
 Teori himpunan merupakan dasar bagi pengembangan dan penerapan matematika
modern yang juga dapat digunakan untuk menjelaskan hubungan antara matematika
dengan filsafat.
 Teori himpunan pertama kali dikemukakan oleh George Boole (1815-1864) yang
kemudian dikembangkan lebih lanjut oleh George F. Cantor (1845-1918).
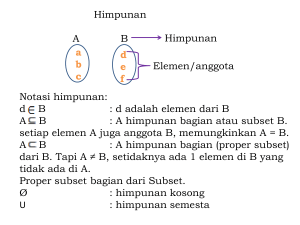
 Himpunan (set) didefinisikan sebagai kumpulan dari objek-objek yang memiliki karakteristik
tertentu, dimana setiap objek secara individual merupakan elemen atau anggota himpunan
bersangkutan. Untuk menunjukkan suatu himpunan digunakan sepasang kurung kurawal {
}.
 Suatu himpunan dinyatakan dengan hurup besar, seperti A, B, C, D, ... sedangkan elemen
himpunan dinyatakan dengan hurup kecil, seperti a, b, c, d, ... Pernyataan bahwa x elemen
himpunan A dituliskan sebagai x  A dan y bukan elemen himpunan A dituliskan sebagai x
 A.
 Untuk menuliskan suatu himpunan dapat digunakan dua cara, yaitu :
1. Cara pendaftaran, yaitu dengan menuliskan semua unsur atau elemen himpunan
2. Cara pencirian, yaitu dengan mendeskripsikan karakteristik umum dari semua elemen
umum himpunan
Misalnya, himpunan semua huruf hidup dalam huruf alfabet (latin)
Cara pendaptaran, A = {a, i, u, e, o}
Cara pencirian, A = {x|x huruf hidup dalam huruf latin}
 Tentukan himpunan-himpunan berikut dengan cara pencirian :
1. A = {1, 4, 9, 16}
2. B = {1, 1/8, 1/27, 1/64}
3. C = {2, 1, 2/3, 1/2, 2/5, 1/3, 2/7}
Jawab :
1. A = { x|x = n2, n bilangan asli < 5}
2. B = { x|x = 1/n3, n bilangan asli < 5}
3. C = { x|x = 2n, n bilangan asli < 5}
 Tentukan himpunan-himpunan berikut dengan cara pendaftaran :
1. D = { x|0 < x < 16, x bilangan ganjil}
2. E = { x|x2 – 1 = 0}
Jawab :
1. D = {1, 3, 5, 7, 9, 11, 13, 15}
2. E = {-1, 1}
 Mungkinkah himpunan B = {-2, 1/3, 4, 7} dapat dituliskan dengan cara pencirian
©Rina Sugiarti
Page 2
Matematika Ekonomi
FEUG
 Jika diketahui himpunan H = { x|x = 3-n, n bilangan cacah}, tentukan apakah anggota
himpunan H tersebut ada yang berupa bilangan cacah ?
 Himpunan kosong (null set) adalah himpunan yang tidak mempunyai anggota dan
dituliskan dengan simbol Ø atau { }
 Himpunan semesta (universe set) adalah himpunan semua elemen yang dibicarakan dan
dituliskan dengan simbol S atau U.
 Bilangan kardinal adalah bilangan yang menunjukkan banyaknya elemen dari suatu
himpunan. Banyaknya elemen himpunan A dituliskan sebagai n(A).
A = {1, 2, 3, 4, 5, 6} → n(A) = 6
B = {a, i, u, e, o} → n(B) = 5
C = {1, 3, 5, 7, 9, 11, 13, 15} → n(C) = 8
 Diagram Venn adalah diagram yang digunakan untuk menggambarkan hubungan
beberapa himpunan secara visual.
 Gambarkan diagram Venn untuk himpunan A dan B jika berlaku :
1. A  B
2. B  A
3. A = B
4. A  B → A dan B bersifat inklusif → A  B  { }
5. A dan B bersifat ekslusif → A  B  { }
Jawab :
1.
S
2.
S
A
B
A
B
3.
S
4.
S
A
A=B
B
A∩B
S
5.
A
B
 Jika A = { x|x2 – 3x + 2 = 0} dan B = {1, 2} apakah A = B ?
Jawab : x2 – 3x + 2 = 0 → (x – 1)(x – 2) = 0 → x = 1 dan x = 2
Karena A = {1, 2} dan B = {1, 2}, maka A = B
©Rina Sugiarti
Page 3
Matematika Ekonomi
FEUG
 Himpunan komplemen adalah himpunan yang memiliki elemen yang tidak termasuk ke
dalam suatu himpunan.
 Jika diketahui himpunan A, maka himpunan komplemen dari A adalah A C = { x|x  A}
S
AC
A  Ac  S
A  Ac  { }
A
 Himpunan bagian (sub set) :
Jika berlaku A  B maka x  A juga berlaku x  B
Jika n(A) = r, maka jumlah subset sebanyak 2r
Diketahui A = {1, 3, 5, 7} maka subset dari A adalah { }, {1}, {3}, {5}, {7}, {1, 3}, {1, 5}, {1,
7}, {3, 5},
{3, 7}, {5, 7}, {1, 3, 5}, {1, 3, 7}, {3, 5, 7}, {1, 5, 7}, {1, 3, 5, 7}
 Operasi himpunan:
1. Gabungan (union): A  B  x x  A atau x  B
2. Irisan (intersection): A  B  x x  A dan x  B
3. Selisih (subtraction): A  B  x x  A dan x  B
4. Pertambahan (addition):
A  B  A  B  A  B  A  B  A  B  A  B
A  B  C  A  B  C  ( A  B  A  C  B  C)  ( A  B  C)
1.
2.
S
A
S
A
B
B
3.
4.
S
B
A
©Rina Sugiarti
B
S
B
A
A
A
B
C
Page 4