Matematika I

Erna Sri Hartatik
Matematika 1
Pertemuan 1
Himpunan
Pembahasan


Kontrak Perkuliahan
Pemahaman Tujuan Perkuliahan
Himpunan
 Pengertian himpunan
 Diagram Venn
Operasi antar Himpunan


Kontrak Perkuliahan
Kontrak kuliah Mtk.doc
GBPP.doc
Berisi:
-Materi kuliah
-aturan perkuliahan
-aturan penilaian
-daftar pustaka
Himpunan
Gerorg Cantor dianggap sebagai bapak teori
himpunan.
Himpunan adalah sekumpulan objek yang mempunyai
syarat tertentu dan jelas.
Objek yang dimaksud dapat berupa bilangan, manusia,
hewan, tumbuhan, negara dan sebagainya.
Objek ini selanjutnya dinamakan anggota atau elemen
dari suatu himpunan .

Suatu himpunan dikatakan baik (well-defined set)
jika mempunyai syarat tertentu dan jelas dalam
menentukan anggota suatu himpunan, ini sangat
penting karena untuk membedakan mana yang
menjadi anggota himpunan dan mana yang bukan
merupakan anggota himpunan
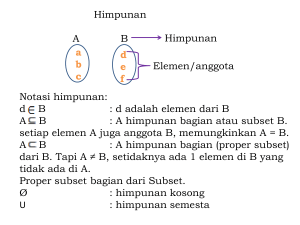
Notasi Himpunan





Dinyatakan dengan huruf besar A, B, C, H, K , dsb
Untuk menyatakan suatu himpunan digunakan
simbol “{….}”.
Untuk melambangkan anggota himpunan biasanya
menggunakan huruf kecil a, b, c, x, y , dsb
Untuk menyatakan anggota suatu himpunan
digunakan lambang “€” (baca: anggota)
Untuk menyatakan bukan anggota suatu himpunan
digunakan lambang “€” (baca: bukan anggota).
Pendefinisian Himpunan

Mendaftarkan semua anggotanya.
Ex: A = {a,e,i,o,u}
B = {2,3,5,7,11,13,17,19}

Menyatakan sifat yang dimiliki anggotanya
Ex: A = Himpunan vokal dalam abjad latin
B = Himpunan bilangan prima yang kurang dari 20

Menyatakan sifat dengan pola
Ex: P = {0,2,4,8,10,…,48}
Q = {1,3,5,7,9,11,13,15,…}

Menggunakan notasi pembentuk himpunan
Ex: P = {x | x himpunan bilangan asli antara 7 dan 15}
(Maksudnya P = {8,9,10,11,12,13,14})
Q = { t | t biangan asli}
(Maksudnya Q = {1,2,3,4,5,6,7,8,9,10,…}
R = { s | s2 -1=0, s bilangan real}
(Maksudnya R = {-1,1})
Macam-macam Himpunan

Himpunan Semesta
adalah himpunan yang anggotanya semua objek
pembicaraan.
Dilambangkan dengan S atau U.

Himpunan Kosong.
adalah himpunan yang tidak mempunyai anggota.
Dilambangkan dengan “Ø” atau { }




Himpunan Bagian
Diberikan himpunan A dan B. Jika setiap anggota A
merupakan anggota B maka dikatakan A
merupakan himpunan bagian (subset) dari B atau
dikatakan B memuat A
Dilambangkan dengan AB.
Jadi AB jika dan hanya jika
xA
xB
Jika ada anggota dari A yang bukan merupakan
anggota B maka A bukan bukan himpunan bagian
dari B,
Dilambangkan dengan AB.
Diagram Venn

Merupakan sebuah metode dalam
merepresentasikan objek-objek diskrit dan
hubungan antara objek-objek tersebut secara
grafis.

Salah satu cara merepresentasikan himpunan
Contoh : S = { a, e, i, o, u }
U = himpunan semua huruf
U
S
a
u
e
i
o
Contoh





N = { 0, 1, 2, 3, …. } = himpunan bilangan natural
Z = { …, -3, -2, -1, 0, 1, 2, 3, …. } = himpunan bilangan
bulat (integer)
Z+ = { 1, 2, 3, …. } = himpunan integer positif
Q = { p/q | p  Z, q  Z, q  0 } = himpunan
bilangan rasional
R = himpunan bilangan nyata (real numbers)
Operasi Himpunan

Gabungan (Union)
 Diberikan himpunan A dan B.
 Gabungan himpunan A dan B ditulis dengan AB
adalah suatu himpunan yang anggotanya berada
di A atau berada di B.
 Jadi AB = { x | xA atau xB }
 Contoh:
A = {a,b,c,1,2} dan B = {c,d,e,f}.
Maka AB = {a,b,c,d,e,f,1,2}

Irisan (Intersection)
 Diberikan himpunan A dan B.
 Irisan himpunan A dan B ditulis dengan AB
adalah suatu himpunan yang anggotanya berada
di A dan juga berada di B.
 Jadi AB = { x | xA dan xB }
 Contoh:
• A = {a,b,c,1,2} dan B = {c,d,e,f}.
Maka AB = {c}
• P = {a,b,c,1,2} dan Q = {d,e,f}.
Maka AB = Ø

Komplemen
 Diberikan suatu himpunan A.
 Komplemen dari A ditulis dengan “ Ac“ adalah
himpunan yang anggotanya berada dalam
himpunan semesta tetapi bukan berada di A.
 Jadi Ac= { x | xS, xA }
 Contoh:
Diberikan semesta himpunan bilangan asli.
Jika A = {0,2,4,6,…} maka Ac = {1,3,5,…}

Power Set
 S adalah himpunan berhingga dengan n anggota
 Maka power set dari S -dinotasikan P(S)- adalah
himpunan dari semua subset dari S dan |P(S)| =
2n
 Contoh: S = { a, b, c}
P(S) = { , {a}, {b}, {c}, {a, b}, {a, c}, {b,
c}, {a, b, c} }
Sifat-sifat operasi

Komutatif
Diberikan himpunan A dan B.
Maka berlaku A  B = B  A dan juga A  B = B  A

Asosiatif
Diberikan himpunan A, B dan C.
Maka berlaku (A  B)  C = A  (B  C) dan
juga (A  B)  C= A (B  C).

Idempoten
Diberikan suatu himpunan A.
Maka berlaku A  A=A dan juga A  A=A

Identitas
Diberikan suatu himpunan A dalam semesta S.
Maka A  S=A dan juga A  S=A

Distributif
Diberikan himpunan A,B dan C.
Maka A (B  C) = (A  B) (A  C) dan
juga A (B  C)=(A  B) (A  C)

Komplementer
Diberikan suatu himpunan A dalam semesta S.
Maka A  Ac= S dan A  Ac = Ø

Dalil De Morgan
Diberikan himpunan A dan B.
Maka (A  B)c = Ac  Bc
dan (A  B)c= Ac  Bc

Prinsip inklusi-eksklusi
 |A  B| = |A| + |B| - |A  B|
 |A  B  C| = |A| + |B| + |C|- |A  B| - |A  C| |B  C| + |A  B  C|
 |A  B  C  D| = |A| + |B| + |C| + |D| - |A  B|
- |A  C| - |A  D| - |B  C| - |B  D| - |C  D|
+ |A  B  C| +|A  B  D| + |A  C  D| +
|B  C  D|
- |A  B  C  D|
Contoh


Dari survei terhadap 270 orang didapatkan hasil sbb.:
 64 suka brussels sprouts,
 94 suka broccoli,
 58 suka cauliflower,
 26 suka brussels sprouts dan broccoli,
 28 suka brussels sprouts dan cauliflower,
 22 suka broccoli dan cauliflower,
 14 suka ketiga jenis sayur tersebut.
Berapa orang tidak suka makan semua jenis sayur yang
disebutkan di atas ?
Jawaban
•
•
•
•
•
•
A = {orang yang suka brussels sprouts }
B = {orang yang suka broccoli }
C = {orang yang suka cauliflower }
|A  B  C|
= |A| + |B| + |C| - |A  B| - |A  C| - |B
 C| + |A  B  C|
= 64 + 94 + 58 – 26 – 28 – 22 + 14 = 154
Jadi mereka yang tidak suka ketiga jenis sayur
tersebut ada sebanyak 270 – 154 = 116 orang
Latihan Soal



Buktikan bahwa (AB)A
Tentukan Power Set dari himpunan dibawah ini:
 {a}
 {a,b}
 {, {}}
Diketahui A={1,2,3,4,5} dan B={0,3,6}. Tentukan:
 AB
 A–B
 AB
 B–A