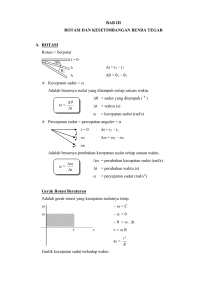
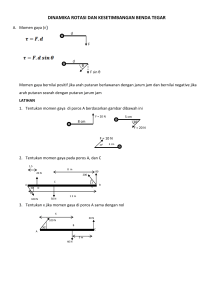
kesetimbangan benda tegar
advertisement

KESETIMBANGAN BENDA TEGAR Kemampuan apa yang akan kalian pelajari di Bab ini? Memformulasikan pengaruh momen/torsi pada sebuah benda dalam kaitannya dengan gerak rotasi benda tersebut. Mengungkap analogi Hukum II Newton tentang gerak translasi dan rotasi. Memformulasikan momen inersia untuk berbagai bentuk benda tegar. Memformulasikan hukum kekekalan momentum sudut pada gerak rotasi. Menganalisis masalah dinamika rotasi benda tegar untuk berbagai keadaan. Menganalisis gerak menggelinding tanpa slip. Benda Tegar (Rigid Body) Dalam dinamika partikel, benda dianggap suatu titik materi (ukuran benda diabaikan). Akibatnya, gaya-gaya yang bekerja pada benda hanya mungkin menimbulkan gerak translasi. Dalam dinamika benda tegar, ukuran benda diperhitungkan, sehingga gayagaya yang bekerja dapat menyebabkan gerak translasi dan rotasi terhadap suatu poros. Gambar 1. Tim akrobatik wanita China mempertahankan keseimbangan agar tidak jatuh. Sumber: en.wuqiaoren.com Ayo Cek Kemampuan Kalian! 1. Masih ingatkah kalian dengan energi mekanik dan hukum kekekalan energi mekanik? 2. Gambarlah diagram gaya pada sistem benda berikut. katrol licin tali balok tali m1 Bidang miring yang kasar m2 balok Torsi/Momen Pengertian Torsi Torsi atau momen gaya, hasil perkalian antara gaya dengan lengan gaya. r F Keterangan: = torsi (Nm) r = lengan gaya (m) F = gaya (N) Jika gaya F yang bekerja pada jarak r arahnya tidak tegaklurus terhadap sumbu rotasi putar benda maka besar torsi pada benda Fr sin Keterangan: = torsi (Nm) r = lengan gaya (m) F = gaya (N) = sudut antara gaya dan sumbu rotasi putar Torsi positif Torsi negatif ( Fi ri ) i Kopel dan Momen Kopel Kopel Kopel, pasangan gayagaya sejajar tetapi berlawanan arah yang mengakibatkan benda berotasi. Kopel terdiri atas 2 buah gaya sebesar F dipisahkan oleh jarak tegak lurus garis kerja kedua gaya d Momen Kopel Besarnya kopel dinyatakan dalam momen kopel, didefinisikan sebagai perkalian antara gaya F dengan jarak kedua gaya d. Kopel positif M Fd Kopel negatif M ( Fi d i ) i Keterangan: M = momen kopel (Nm) F = gaya (N) R = jarak antara kedua gaya (m) Momen Inersia Momen Inersia Partikel Momen inersia, sebuah partikel bermassa m yang melakukan gerak rotasi atau gerak orbital pada jarijari lintasan r adalah I mr Keterangan: I = momen inersia (kgm2) m = massa partikel (kg) r = jari-jari lintasan (m) 2 Hubungan langsung antara percepatan sudut dengan torsi yang diberikan adalah I Keterangan: τ = torsi (Nm) α = percepatan sudut (rad/s2) Momen Inersia Benda Tegar Benda tegar, benda yang tidak mengalami perubahan bentuk atau volume akibat bekerjanya gaya pada benda tersebut. Momen Inersia Beberapa Benda Dinamika Gerak Rotasi Pusat Massa • Titik pusat massa, titik yang bergerak dalam lintasan yang sama dengan yang dilewati partikel jika mendapat gaya yang sama. • Pusat koordinat titik pusat massa suatu benda panjang (1 dimensi) ditentukan sebagai berikut. pm = (Xpm ; Ypm) X pm mi xi i mi i Ypm mi yi i mi i Gerak Rotasi Benda Tegar Hukum II Newton untuk gerak rotasi dapat dinyatakan sebagai berikut “ Besar torsi resultan sama dengan momen inersia dikalikan percepatan sudut.” I Keterangan: = torsi pada benda (Nm) I = momen inersia benda (kgm2) = percepatan sudut benda (rad/s2) Katrol Dengan anggapan bahwa antara katrol dengan tali tidak terjadi selip, torsi resultan pada katrol adalah rT 1 rT2 Keterangan: r = jari-jari katrol (m) T = tegangan tali (N) Hubungan percepatan linier dengan percepatan sudut gerak rotasi katrol adalah a r Keterangan: a = percepatan gerak beban (m/s2) = percepatan sudut katrol Hukum II Newton untuk gerak kedua beban m1 dan m2 dapat dinyatakan dengan persamaan m1 g T1 m1a T2 m2 g m2 a Dengan menjumlahkan kedua persamaan di atas diperoleh, m1 m2 a g m1 m2 I r2 Gerak Menggelinding • Suatu benda yang menggelinding tanpa selip, melibatkan gerak translasi dan rotasi. • Hubungan sederhana antara laju linier v dengan kecepatan sudut pada benda yang menggelinding berjari-jari r dinyatakan dengan v r Keterangan: v = laju linier (m/s) = kecepatan sudut (rad/s2) R = jari-jari (m) Gerak Menggelinding pada Bidang Horizontal Gerak translasi silinder: F fs ma Gerak rotasi silinder: I Torsi penyebab gerak rotasi silinder hanya ditimbulkan oleh gaya gesek statis maka: rf s • Gaya gesek statis yang terjadi dapat bervariasi tergantung pada besarnya momen inersia I, percepatan a, dan jari-jari r a fs I 2 r • Percepatan gerak translasi silinder dapat ditulis dalam persamaan: a F I m 2 r • Percepatan translasi silinder pejal yang menggelinding adalah Keterangan: a = percepatan linier (m/s2) F = gaya penggerak (N) I = momen inersia (kg m2) r = jari-jari (m) m = massa (kg) 2F a 3m Gerak Menggelinding pada Bidang Miring • Gerak translasi silinder yang tidak mengalami selip: mg sin fs ma • Gerak rotasi silinder: • Percepatan gerak translasi silinder: mg sin a I r2 m a I r Percepatan translasi silinder pejal yang menggelinding tanpa selip sepanjang bidang miring dengan sudut kemiringan terhadap horizontal Ө adalah 2 g sin a 3 Keterangan: a = percepatan gerak translasi (m/s2) m = massa (kg) g = percepatan gravitasi (m/s2) Ө = sudut kemiringan bidang ( °) I = momen inersia (kg m2) r = jari-jari (m) Momentum Sudut Pengertian Momentum Sudut Sebuah benda bermassa m berotasi pada sumbu tetap dengan kecepatan sudut sehingga memiliki momen inersia I, besar momentum sudutnya: L I Keterangan: L = momentum sudut (kg m2/s) I = momentum inersia (kg m2) = kecepatan sudut (rad/s) Hukum Kekekalan Momentum Sudut “Momentum sudut total pada benda yang berotasi, tetap konstan jika torsi total yang bekerja padanya sama dengan nol.” I11 I 22 I konstan Aplikasi hukum kekekalan momentum sudut Keseimbangan Benda Tegar Keseimbangan Statis dan Dinamis • Sebuah benda berada dalam keadaan setimbang jika benda tersebut tidak mengalami percepatan linier ataupun percepatan sudut. • Benda yang diam merupakan benda yang berada pada kesetimbangan statis. • Benda yang bergerak tanpa percepatan merupakan benda yang berada pada kesetimbangan dinamis. Syarat Kestimbangan Benda Tegar F 0 Pada kondisi ini, kemungkinan keadaan benda adalah: a. diam (kesetimbangan statis), dan b. bergerak dengan kecepatan linier tetap (kesetimbangan dinamis). 0 Pada kondisi ini kemungkinan keadaan benda adalah: a. diam (kesetimbangan statis), dan b. berotasi dengan kecepatan sudut tetap (kesetimbangan dinamis). Macam-Macam Kestimbangan Benda Tegar a. Kesetimbangan Stabil Ketimbangan stabil, kesetimbangan yang dialami benda, dimana jika pada benda diberikan gangguan yang mengakibatkan posisi benda berubah, setelah gangguan tersebut dihilangkan, benda akan kembali ke posisi semula b. Kesetimbangan Labil Kesetimbangan labil, kesetimbangan yang dialami benda, di mana jika pada benda diberikan ganguan yang mengakibatkan posisi benda berubah, dan setelah gangguan tersebut dihilangkan maka benda tidak kembali ke posisi semula. c. Kesetimbangan Indiferen Kesetimbangan indiferen, kesetimbangan yang dialami benda di mana jika pada benda diberikan gangguan yang mengakibatkan posisi benda berubah, dan setelah gangguan tersebut dihilangkan, benda tidak kembali ke posisi semula, namun tidak mengubah kedudukan titik beratnya. Contoh Soal 1. Tentukan tegangan tali pengikat beban di bawah 300 T2 600 T1 8 kg Jawab. Nilai tegangan tali T1 = ? W cos T1 sin ( ) Nilai tegangan tali T2 = ? 8.10 cos 30 T1 sin ( 30 60 ) 1 80 . 3 2 T1 1 W cos T2 sin ( ) 80 cos 60 T2 sin (30 60 ) 1 80. 2 T2 1 T1 40 3 T2 40 N 2. Tentukan besar gaya F agar sistem setimbang 300 600 F 60 kg Perhatikan uraian vektor pada sistem itu. Y T1 300 600 T2 F 60 kg Jawab. T1 T2 = W = m. g = 600 N T1x T1 y T 2y 300 600 T2 x F T2 Sumbu x Fx Sumbu y. Fy 0 T2 x – T1x = 0 T1 y + T2 y – F = 0 T2 sin 60 = T1 sin 30 T1 cos 30 + T2 cos 60 = F T2 . ½ 3 = T1 ½ ½ T1 = 600 3 N …..1 F = ½ T1 = T2 3 0 F = T1 + ½ 3 T2 = F . 600 F = 3. 600 + 600 F = 2400 N T1 + ½ 3 T2 + 3600 3