ROTASI BENDA TEGAR

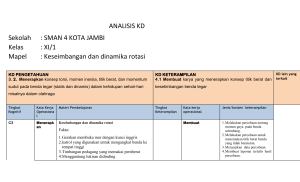
ROTASI
BENDA TEGAR
KECEPATAN SUDUT
DAN PERCEPATAN SUDUT
lintasan titik P
Panjang busur lintasan : s  rq
Posisi sudut :
q s r
P
r
q
r q2
q1
(10.1b)
Kecepatan sudut rata-rata :
q  q q
 2 1
t
t2  t1
Kecepatan sudut sesaat :
q
dq
  lim

dt
t 0 t
Percepatan sudut rata-rata :
Q,t2
r
(10.1a)
P,t1
(10.2)
(10.3)

t
(10.4)
 d

dt
t 0 t
(10.5)

 2  1
t2  t1

Percepatan sudut sesaat :
  lim
GERAK ROTASI UNTUK PERCEPATAN SUDUT TETAP
konstan

 (t )
t
o d  0 dt
d
dt
 (t )  o  t
 (t )  o  t

dq
dt
(10.6)
q (t )
t
qo dq  0 dt
q (t )
t
qo dq  0 (o  t )dt
q (t )  q o  ot  12 t 2 (10.7)
 2  o2  2 (q  qo ) (10.8)
GLBB
v(t )  vo  at
s(t )  so  vot  12 at 2
v 2  vo2  2a ( s  so )
Adakah relasi antara besaran sudut dan besaran linier ?
RELASI BESARAN SUDUT DAN LINIER

v
P
r
q
Kecepatan linier :
ds
v
dt
s  rq
panjang lintasan
vr
dq
dt
v  r
(10.9)
Percepatan tangensial :
at 

at
a
ar
P
d
dv
r
dt
dt
at  r
Percepatan radial :
v2
ar 
 r 2
r
(10.10)
(10.11)
a  at2  ar2  r 2 2  r 2 4  r  2   4 (10.12)
ENERGI KINETIK ROTASI
Energi kinetik partikel ke i :
K i  12 mi vi2

vi
ri
q
vi  ri
Energi kineti seluruh benda :
mi
K   Ki   12 mi vi2  12  mi ri2 2


K  12  mi ri2  2
m
(10.13)
Momen kelembaman
I   mi ri2
(10.14)
K  12 I 2
(10.15)
Momen kelembaman untuk benda pejal :
rapat massa :
m dm
  lim

V 0 V
dV
I  lim  r 2 m   r 2 dm
m  0
dm  dV
I   r 2dV
(10.16)
Teorema Sumbu Sejajar
Jika Ic adalah momen kelembaman benda terhadap sumbu putar yang melalui
pusat massanya, maka momen kelembaman benda terhadap sembarang
sumbu putar yang sejajar dan berjarak d dari sumbu tersebut adalah :
I  I c  Md 2
C
d
O
(10.17)
MOMEN GAYA
F3
F1
r3
d1
  rF sin 
r sin   d
  Fd
(10.18)
 net  1   2  F1d1  F2d 2
r1
Bagaimana keterkaitan momen gaya dengan besaran sudut ?
d2
r2

F2
F2 sin 
Ft
r
m
F2 cos 
  Ft r
Ft  mat
  (mat )r
at  r
  (mr )r
  (mr 2 )
  I
(10.19)
Usaha dan Energi
F
F sin

Usaha :
dW  F  ds  ( F sin  )rdq
dW   dq
ds
dq

P
  I  I
d
d
d dq
I
I

dt
dq
dq dt
dW  I d
t
W   I d
o
 12 It2  12 Io2
Usaha yang dilakukan oleh gaya luar untuk memutar benda tegar terhadap
sumbu tetap sama dengan perubahan energi kenetik rotasi benda tersebut !
KESETIMBANGAN
Kest. Translasi, Kest Rotasi, dan
Kest. Statis
Syarat Kesetimbangan untuk Benda Tegar
F
F”
Benda tegar
r
CM
F’
Apa yang terjadi jika terdapat gaya yang bekerja padanya ?
τ  rF
(12.1)
Pengaruh gaya pada benda tegar bergantung pada :
 Bentuk dan ukuran benda
 Berbagai gaya yang bekerja padanya
 Titik tangkap masing-masing gaya
Bilamana benda dikatakan dalam kesetimbangan ?
Kesetimbangan translasi
1. Jika resultan gaya luar nol
F  0
(12.2)
Kesetimbangan rotasi
2. Jika resultan momen gaya luar nol
τ  0
(12.3)
Kesetimbangan statis
vcm  0 dan   0