Titik Berat Benda Titik berat benda

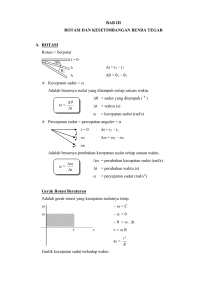
KESETIMBANGAN
Momen Gaya ( τ )
Momen gaya atau torsi adalah besaran yang dapat menyebabkan
benda berotasi atau berputar.
Besar momen gaya didefinisikan sebagai hasil kali antara gaya yang
bekerja dengan lengan. Momen gaya termasuk dalam besaran vektor.
τ =rxF
dengan:
τ = momen gaya (Nm).
r = jarak sumbu rotasi ke titik tangkap gaya (m),
F = gaya yang bekerja pada benda (N).
Contoh soal :
Perhatikan gambar di bawah ini!
Berdasarkan gambar tersebut, tentukan
a. τ1, τ2, τ3, dan τ4!
b. Jumlah total torsi yang bekerja!
c. Ke mana arah batang mengguling?
Penyelesaian
Diketahui :
F1 = 4 N r1 = 1 m
F2 = 5 N r2 = 2 m
F3 = 5 N r3 = 1 m
F4 = 4 N r4 = 2 m
1
Ditanyakan :
a. τ1, τ2, τ3, dan τ4 = ...?
b. ∑τ = ...?
c. Arah batang mengguling?
Jawab :
a. Kita tetapkan bahwa arah mengguling searah putaran jarum
jam bernilai positif.
τ1 = - F1 · r1 = - 4 · 1 = - 4 Nm
τ2 = F2 · r2 = 6 · 2 = 12 Nm
τ3 = - F3 · r3 = - 5 · 1 = - 5 Nm
τ4 = F4 · r4 = 4 · 2 = 8 Nm
b. Σ τ = τ1 + τ2 + τ3 + τ4
= -4 + 12 + (-5) + 8
= 20 - 9
= 11 Nm
c. Benda akan mengguling searah jarum jam, karena Στ = 11
Nm (bernilai positif)
Apabila gaya F yang bekerja pada benda membentuk sudut tertentu
dengan lengan gayanya (r), maka
τ = r F sin α
dimana :
τ = momen gaya (Nm)
r = lengan gaya (m)
F = gaya yang bekerja (N)
α = sudut antara garis kerja gaya (F) dan lengan gaya (r).
2
Apabila pada sebuah benda bekerja beberapa gaya, maka jumlah
momennya sama dengan momen gaya dari resultan semua gaya yang
bekerja
pada benda tersebut.
Σ τ = τ1 + τ2 + τ3 + ....
Contoh soal :
Pada sebuah benda bekerja gaya 20 N seperti pada gambar.
Jika titik tangkap gaya berjarak 25 cm dari titik P, berapakah besar momen
gaya terhadap titik P?
Penyelesaian :
Diketahui:
F = 20 N
r = 25 cm = 0,25 m
α = 150°
Ditanyakan : τ = ....?
Jawab :
τ = r F sin α
= (0,25 m)(20 N)(sin 150°)
1
2
= (0,25 m)(20 N)( )
= 2,5 Nm.
Pusat Massa
Benda tegar yang melakukan gerak rotasi, memiliki pusat massa
yang tidak melakukan gerak translasi (v = 0).
Letak pusat massa suatu benda menentukan kestabilan
(kesetimbangan) benda tersebut. Jika dari titik pusat massa benda ditarik
garis lurus ke bawah dan garis tersebut jatuh pada bagian alas benda,
dikatakan benda berada dalam keadaan setimbang stabil. Namun, apabila
garis lurus yang ditarik dari titik pusat massa jatuh di luar alas benda maka
benda dikatakan tidak stabil.
3
Jika kita memiliki sebuah sistem yang terdiri atas 2 massa, massa 1
di titik x1 dan massa 2 ditik x2. Pusat massa sistem terletak di titik tengah.
x pm 
x1m 1  x 2 m 2
m1  m 2
Bila sistem terdiri atas banyak benda bermassa maka pusat massa sistem
adalah:
N
xpm
x m  x 2m 2  ...  xn m n
 1 1

m1  m 2  ...  m n
x m
n
n
n 1
N
m
n
n 1
N
y pm
y m  y 2m 2  ...  y n m n
 1 1

m1  m 2  ...  m n
y m
n
n
n1
N
m
n
n1
N
z pm
z m  z 2m 2  ...  z n m n
 1 1

m1  m 2  ...  m n
z m
n
n
n 1
N
m
n
n 1
4
Contoh soal :
Sebuah sistem terdiri atas dua massa masing-masing bermassa 3 kg.
Massa 1 terletak di titik (0,0), masa kedua di titik (0,4) di manakah pusat
massa benda?
Penyelesaian :
x m  x 2 m 2 (0)(3)  (0)(3)
x pm  1 1

0
m1  m 2
3 3
y m  y2 m 2 (0)(3)  (4)(3)
y pm  1 1

2
m1  m 2
33
Pusat massa terletak di tengah kedua benda tersebut atau
berada pada (0 , 2)
Titik Berat Benda
Titik berat benda adalah titik tangkap gaya berat suatu benda, di
mana titik tersebut dipengaruhi oleh medan gravitasi.
Jika benda tersebut berada dalam medan gravitasi maka masingmasing partikel tersebut mempunyai berat (w1, w2, w3, w4, wn).
Resultan dari gaya berat dari masing-masing partikel itulah yang
kemudian disebut dengan berat benda (w) dan titik tangkap gaya berat itu
disebut dengan titik berat (Zo).
Menentukan letak titik berat :
a. Bangun dan bidang simetris homogen
Untuk bangun atau bidang simetris dan homogen titik beratnya
berada pada titik perpotongan sumbu simetrinya. Contohnya : bujur
sangkar, balok kubus dan bola.
5
b. Bangun atau bidang lancip
Untuk benda ini titik beratnya dapat ditentukan dengan digantung
benang beberapa kali, titik potong garis-garis benang (garis berat)
itulah yang merupakan titik beratnya. Dari hasil tersebut ternyata
dapat diketahui kesamaannya seperti berikut.
c. Bagian bola dan lingkaran
Untuk bagian bola yaitu setengah bola pejal dan bagian lingkaran
yaitu setengah lingkaran dapat dilihat pada Gambar berikut.
d. Gabungan benda
Untuk gabungan benda-benda homogen, letak titik beratnya dapat
ditentukan dari rata-rata jaraknya terhadap acuan yang ditanyakan.
Rata-rata tersebut ditentukan dari momen gaya dan gaya berat.
6
N
x w  x 2 w 2  ...  xn w n
x0  1 1

w 1  w 2  ...  w n
x w
n
n
n1
N
w
n
n 1
N
y w  y 2 w 2  ...  y n w n
y0  1 1

w 1  w 2  ...  w n
y w
n
n
n 1
N
w
n
n 1
N
z 1w 1  z 2 w 2  ...  z n w n 
z0 
 n1N
w 1  w 2  ...  w n
znwn
w
n
n1
Pada benda-benda homogen (massa jenisnya sama) w dapat diubah seperti
berikut.
 Bila diketahui massanya:
N
N
x m
n
x0 
n 1
N
m
n 1
y m
n
n
y0 
n
N
n 1
N
m
n 1
z m
n
n
z0 
n
n
n 1
N
m
n
n 1
7
 Bila diketahui volumnya:
N
N
x V
n
x0 
y V
n
n1
N
N
n
y0 
V
z
n
n1
N
z0 
V
n
Vn
n1
N
V
n
n1
n
n
n1
n 1
 Bila diketahui luas permukaannya:
N
N
x A
n
x0 
y
n
n1
N
y0 
A
N
n
n 1
N
z0 
A
n
n1
z
An
n
An
n1
N
A
n
n1
n
n1
 Bila benda berbentuk garis:
N
N
x L
n
x0 
n 1
N
L
n 1
y L
n
n
y0 
n
N
n 1
N
L
n 1
z L
n
n
z0 
n
n
n 1
N
L
n
n 1
Contoh soal :
Sebuah karton homogen berbentuk L ditempatkan pada sistem koordinat
seperti gambar berikut.
Tentukan titik berat karton tersebut!
Penyelesaian
Untuk menentukan titik beratnya, karton bentuk L tersebut dapat
dianggap sebagai dua benda.
Benda I : Z1 (20, 10) → A1 = 40 . 20 = 800 cm2
Benda II : Z2 (50, 20) → A2 = 20 . 40 = 800 cm2
8
Titik berat benda memenuhi:
x A  x 2 A 2 20.800  50.800
x0  1 1

 35 cm
A1  A 2
800  800
y A  y2 A 2 10.800  20.800
y0  1 1

 15 cm
A1  A 2
800  800
Berarti Zo = (35 , 15) cm
Kesetimbangan
Benda dikatakan dalam keadaan kesetimbangan bila gaya dan torsi
pada benda adalah nol, maka benda tidak akan mengalami perubahan
gerak maupun rotasi.
Secara umum, benda dapat mengalami gerak translasi, gerak rotasi
atau gerak translasi sekaligus rotasi (menggelinding).
 Gerak translasi disebabkan oleh gaya.
 Gerak rotasi disebabkan oleh momen gaya.
a. Syarat benda akan translasi adalah ΣF ≠ 0 dan τ = 0
b. Syarat benda akan rotasi adalah ΣF = 0 dan τ ≠ 0.
c. Syarat benda menggelinding adalah ΣF ≠ 0 dan τ ≠ 0.
Macam-macam Kesetimbangan
a. Kesetimbangan stabil.
jika benda diberi gangguan dari sikap setimbangnya maka ia
akan kembali ke kedudukannya semula. Ini terjadi jika dalam
gangguan tersebut titik berat berpindah ke atas.
9
b. Kesetimbangan labil,
jika benda diberi gangguan dari sikap setimbangnya, maka ia
tidak akan kembali kedudukan semula. Ini terjadi jika dalam
gangguan tersebut titik berat berpindah ke bawah.
c. Kesetimbangan netral (indeferen)
jika benda diberi gangguan dari sikap setimbangnya, maka
dalam kedudukan barunya ia tetap setimbang. Ini terjadi jika
dalam gangguan tersebut titik beratnya tingginya tetap.
10