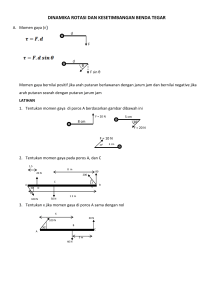
dinamika rotasi dan keseimbangan benda tegar
advertisement
FISIKA XI SMA 3 Magelang @iammovic Standar Kompetensi: Menerapkan konsep dan prinsip mekanika klasik sistem kontinu dalam menyelesaikan masalah Kompetensi Dasar: Merumuskan hubungan antara konsep torsi, momentum sudut, dan momen inersia, berdasarkan hukum II Newton serta penerapannya dalam masalah benda tegar Momen gaya atau torsi adalah ukuran keaktifan sebuah gaya yang bekerja pada suatu benda untuk memutar benda tersebut terhadap suatu titik poros tertentu. Jika sudut antara r dan F adalah πΌ, maka besar momen gaya adalah : π = ππ π¬π’π§ πΆ atau π = π πππ πΆ π π sin πΌ = π , dimana disebut lengan momen. Sehingga besar momen gaya dapat dinyatakan sebagai hasil kali lengan momen dan besar gaya : π = π. π Contoh : - Sebuah gaya πΉ = 120 π π + 180 π π dikerjakan pada suatu benda pada suatu titik yang memiliki vector kedudukan π = 3 π π − 2 π π terhadap acuan πΆ. Hitunglah momen yang dikerjakan gaya ini terhadap titik πΆ. Momen adalah hasil kali vector antara vector titik tangkap gaya π dan vector gaya π, yaitu π = π π π. Untuk vector yang hanya dinyatakan dalam π dan π, π lebih cepat ditentukan dengan aturan π x π = π dan π x π = −π. Jadi, π = π π π = 3 π − 2 π π₯ 120 π + 180 π = 540 +π − 240 −π = πππ π Momen gaya total pada suatu benda yang disebabkan oleh dua buah gaya atau lebih yang bekerja terhadap suatu poros : π = π1 + π2 + π3 … + ππ Catatan : 1. Lengan momen π adalah panjang garis yang ditarik dari titik poros sampai mendorong tegak lurus garis kerja vector gaya πΉ. 2. Arah momen gaya π dinyatakan oleh arah putaran vector gaya πΉ terhadap titik poros. Arah positif momen ditetapkan sembarang, tetapi umumnya ditetapkan momen yang menghasilkan putaran searah jarum jam adalah positif (+) dan yang berlawanan arah jarum jam adalah negative (-). Contoh : - Batang AB yang panjangnya 2 m dipengaruhi tiga gaya seperti pada gambar. Tentukan torsi batang tersebut di titik O. π = −π1 + π2 + π3 = − 120 π 1 π sin 30° + 100 π 0,5 π + 150 π 1 π sin 37° = −60 π. π + 50 π. π + 90,3 π. π = β― π. π Karena torsi analog dengan gaya F, dan percepatan sudut analog dengan percepatan linier, apakah torsi berkaitan dengan percepatan sudut dari gerak rotasi? π = ππ Karena π sama denganπΉ. πΆ, maka : π = π. πΉ. πΆ Dengan mengalikan kedua ruas dengan πΉ, maka : πΉ. π = π. πΉπ . πΆ Karena πΉ. π adalah Torsi dan π. πΉπ adalah Momen Inersia, jadi : π π = π°. πΆ = π° πΉ Besaran yang menyatakan ukuran kelembaman benda yang mengalami gerka rotasi. Momen inersia π° dari sebuah partikel bermassa π dan berjarak π dari poros putar dinyatakan oleh : π° = πππ Momen inersia dari beberapa partikel (titik massa) terhadap suatu poros diperoleh dengan menjumlahkan secara aljabar biasa tiap-tiap momen inersia. ππ πππ π°= π Contohnya, momen inersia dari tiga buah partikel terhadap suatu poros adalah : πΌ = 3π=1 ππ ππ2 = π1 π12 +π2 π22 +π3 π32 Contoh : Tiga buah benda masing-masing bermassa 0,6 kg diikatkan pada batang, yang massanya dapat diabaikan seperti pada gambar. Tentukan momen inersia sistem terhadap poros rotasi melalui ujung batang. πΌ = 3π=1 ππ ππ2 = π1 π12 +π2 π22 +π3 π32 *dari soal, π1 = π2 = π3 = π = 0,6 ππ π1 = 10 ππ = 10π₯10−2 π π2 = 10 + 15 ππ = 25π₯10−2 π π1 = 25 + 20 ππ = 45π₯10−2 π Jadi, πΌ = π1 π12 +π2 π22 +π3 π32 = π π12 + π22 + π32 = 1,65π₯10−1 πππ2 Contoh : Roda tipis berjari – jari 30 cm dan massa 1 kg menggelinding bersama bola pejal berjari – jari 8 cm dan bermassa 1,5 kg. Tentukan perbandingan momen inersia bola dan roda. πππππ = 1 ππ π ππππ = 30 cm = 0,3 m πππππ = 1,5 ππ π ππππ = 8 cm = 0,08 m Jawab: πΌππππ = ππ 2 = 1 ππ 0,3 π 2 = 1 ππ 0,09 π2 = 0,09 ππ. π2 πΌππππ = ππ 2 = 1,5 ππ 0,08 π 2 = 1,5 ππ 0,0064 π2 = 0,0096 ππ. π2 πΌππππ 0,09 3 = = πΌππππ 0,0096 0,32 Sebuah kopel adalah sepasang gaya sejajar yang sama besar tetapi arahnya berlawanan. Kopel tidak menghasilkan gerak translasi karena resultan gaya sama dengan nol πΉ = 0 , tetapi kopel akan menghasilkan momen kopel yang menyebabkan gerak rotasi. Besar momen kopel, π, adalah hasil kali antara besar gaya πΉ dengan jarak π antara kedua pasangan gaya. Kopel yang menghasilkan putaran searah jarum jam ditetapkan bertanda positif dan sebaliknya negatif. Momentum sudut didefinisikan sebagai perkalian antara momen inersia dan kecepatan sudut. Secara matematis, ditulis sebagai berikut : π³ = π°. π Jika lengan Torsi dan kecepatna linier diketahui, maka π£ 2 πΏ = πΌπ = ππ π π³ = π. π. π Momentum sudut merupakan besaran vektor karena memiliki besar dan arah. Arah momentum sudut dapat ditentukan dengan aturan tangan kanan. “Jika tidak ada momen gaya luar yang bekerja pada suatu system yang mengalami gerak rotasi πππ’ππ , maka momentum sudut system selalu tetap. πΏπ ππ π‘ππ = 0 πΏ1 = πΏ2 π°π ππ = π°π ππ Menggelinding merupakan perpaduan gerak translasi dan rotasi sebuah benda (tanpa selip). Dalam melakukan gerak menggelinding, dibutuhkan gaya gesek antara benda dengan permukaan. Jika tidak ada gaya gesek maka benda tersebut akan tergelincir atau slip (benda hanya melakukan gerak translasi). Ketika sedang menggelinding, benda memiliki energi kinetik yang terbagi 1 2 atas dua jenis, yaitu energi kinetik translasi πΈπΎπππππ πππ π = ππ£ 2 dan energi kinetik rotasi πΈπΎπ ππ‘ππ π = 1 πΌπ2 2 . Jadi energi totalnya : π π π π π¬π²π»ππππ = π¬π²π»ππππππππ + π¬π²πΉπππππ = ππ + π°π π π Jika resultan momen gaya luar yang bekerja pada benda sama dengan nol (tidak ada momen gaya luar yang bekerja pada benda), pada gerak rotasi tersebut berlaku Hukum Kekekalan Energi Mekanik : βπ¬π· = βπ¬π²π»ππππππππ + βπ¬π²πΉπππππ 1. Gerak Menggelinding Pada Bidang Datar (kasar) Pada Gerak Translasi berlaku Hukum II Newton, πΉ = π. π π − π = π. π * π = Gaya gesek Pada Gerak Rotasi berlaku : π = π°. πΆ 2. Gerak Menggelinding Pada Bidang Miring (Kasar) Pada Gerak Translasi berlaku Hukum II Newton, πΉ = π. π : π. π sin π½ − π = π. π Pada Gerak Rotasi berlaku : π = π°. πΆ MACAM-MACAM KESEIMBANGAN KESEIMBANGAN STATIS Ada 3 macam keseimbangan statis, semua dapat diperkirakan dengan memperhatikan apa yang terjadi dengan kedudukan titik beratnya ketika benda diberi gangguan kecil. • Keseimbangan labil : Jika setelah gangguan kecil dihilangkan, titik berat bergerak ke bawah. • Keseimbangan stabil : Jika setelah gangguan kecil dihilangkan, titik berat bergerak ke atas. • Keseimbangan netral (indeferen) Jika titik berat selalu berada pada ketinggian yang tetap. KESETIMBANGAN STABIL KESETIMBANGAN LABIL KESETIMBANGAN INDEFEREN MACAM-MACAM KESEIMBANGAN KESEIMBANGAN DINAMIS • Keseimbangan translasi : Keseimbangan yang dialami benda ketika bergerak tanpa mengalami percepatan linier π = π, π = πππππ . • Keseimbangan rotasi : Keseimbangan yang dialami benda ketika bergerak tanpa mengalami percepatan sudut πΆ = π, π = πππππ . SYARAT-SYARAT KESEIMBANGAN 1. Resultan gaya pada benda = 0 πΉ=0 Pada kondisi ini, kemungkinan keadaan benda adalah: a. Diam (kesetimbangan statis), dan b. Bergerak dengan kecepatan linier tetap (kesetimbangan dinamis). 2. Resultan torsi pada benda = 0 π=0 Pada kondisi ini kemungkinan keadaan benda adalah: a. Diam (kesetimbangan statis), dan b. Berotasi dengan kecepatan sudut tetap (kesetimbangan dinamis). KESEIMBANGAN Contoh : Batang AC bermassa 40 kg dan panjangnya 3 m. Jarak tumpuan A dan B adalah 2 m (di B papan dapat berputar) seorang anak bermassa 25 kg berjalan dari A menuju C. Berapa jarak minimum anak dari titik C agar papan tetap setimbang (ujung batang A hampir terangkat)? π=0 π€π΄πΆ π·π΅ = ππ΄πππ 1 − π₯ 400 0,5 = 250 1 − π₯ 200 = 250 − 250π₯ 250π₯ = 50 π₯ = 0,2 π KESEIMBANGAN Contoh : Pada sistem kesetimbangan benda tegar seperti pada gambar di samping, batang AB homogen dengan panjang 80 cm, beratnya 18 N, menyangga beban seberat 30 N, BC adalah tali. Berapakah tegangan pada tali (dalam newton) jika jarak AC = 60 cm? π΅πΆ = π΄π΅2 + π΄πΆ 2 = 802 + 602 = 100 ππ 60 sin πΌ = = 0,6 100 Syarat kesetimbangan di titik A : ππ΄ = 0 1 π΄π΅ − 30 π΄π΅ = 0 2 π 48 − 18 40 − 30 80 = 0 48π − 720 − 2400 = 0 3120 π= = 65 π 48 π π΄π΅ sin πΌ − 18 KESEIMBANGAN TIGA GAYA Syarat keseimbangan statis untuk tiga gaya sebidang yang bekerja pada suatu sistem partikel, adalah : πΉ1 πΉ2 πΉ3 = = sin πΌ sin π½ sin πΎ *dimana πΌ + π½ + πΎ = 360° KESEIMBANGAN TIGA GAYA Contoh : Benda pada gambar memiliki berat 400 N dan digantung dalam keadaan diam. Tentukanlah besar tegangan yang terjadi pada kedua tali yang menahan benda. (Ingat, tegangan adalah gaya yang terdapat pada seutas tali yang menarik suatu benda). π»π π»π ππ π1 π2 π€3 = = → = = πππ πΆπ πππ πΆπ πππ πΆπ sin 143° sin 127° sin 90° π1 π2 400 = = 0,6 0,8 1 π»π =240 N, π»π = πππ π΅ KESEIMBANGAN TIGA GAYA Contoh : Seutas tali ABCD digantungkan pada titik A dan D. Pada titik C digantungkan beban seberat w. Tentukanlah besar w agar sistem dalam kesetimbangan. Titik B Titik C π» πππ ππ°+ππ° π 1 2 12 =1 3 2 = ππ πππ ππ°+ππ° →π =4 3π π» πππ ππ°+ππ° 4 3 1 2 3 = π€ 1 2 = ππ πππ ππ°+ππ° →π€ =4π TITIK BERAT Titik berat adalah suatu titik dalam suatu benda (dapat juga di luar benda) dimana gaya berat benda bekerja secara efektif. 1. Titik berat benda homogen (massa jenis sama dalam keseluruhan sistem) yang bentuknya teratur, terletak pada perpotongan diagonalnya. 2. Titik berat benda gabungan dari benda-benda teratur bentuknya, dapat ditentukan dengan koordinat ππ , ππ . Jika diketahui : • Berat tiap partikel : π€1 π₯1 + π€2 π₯2 + π€3 π₯3 + β― + π€π π₯π π₯0 = π€1 + π€2 + π€3 + β― + π€π π€1 π¦1 + π€2 π¦2 + π€3 π¦3 + β― + π€π π¦π π¦0 = π€1 + π€2 + π€3 + β― + π€π TITIK BERAT • Benda berbentuk bidang datar : • Benda berbentuk bangun ruang: • Benda berbentuk kurva : π΄1 π₯1 + π΄2 π₯2 + π΄3 π₯3 + β― + π΄π π₯π π₯0 = π΄1 + π΄2 + π΄3 + β― + π΄π π΄1 π¦1 + π΄2 π¦2 + π΄3 π¦3 + β― + π΄π π¦π π¦0 = π΄1 + π΄2 + π΄3 + β― + π΄π π1 π₯1 + π2 π₯2 + π3 π₯3 + β― + ππ π₯π π₯0 = π1 + π2 + π3 + β― + ππ π1 π¦1 + π2 π¦2 + π3 π¦3 + β― + ππ π¦π π¦0 = π1 + π2 + π3 + β― + ππ π1 π₯1 + π2 π₯2 + π3 π₯3 + β― + ππ π₯π π₯0 = π1 + π2 + π3 + β― + ππ π1 π¦1 + π2 π¦2 + π3 π¦3 + β― + ππ π¦π π¦0 = π1 + π2 + π3 + β― + ππ @iammovic
