BAB XVIII KESEBANGUNAN dan KONGRUENSI

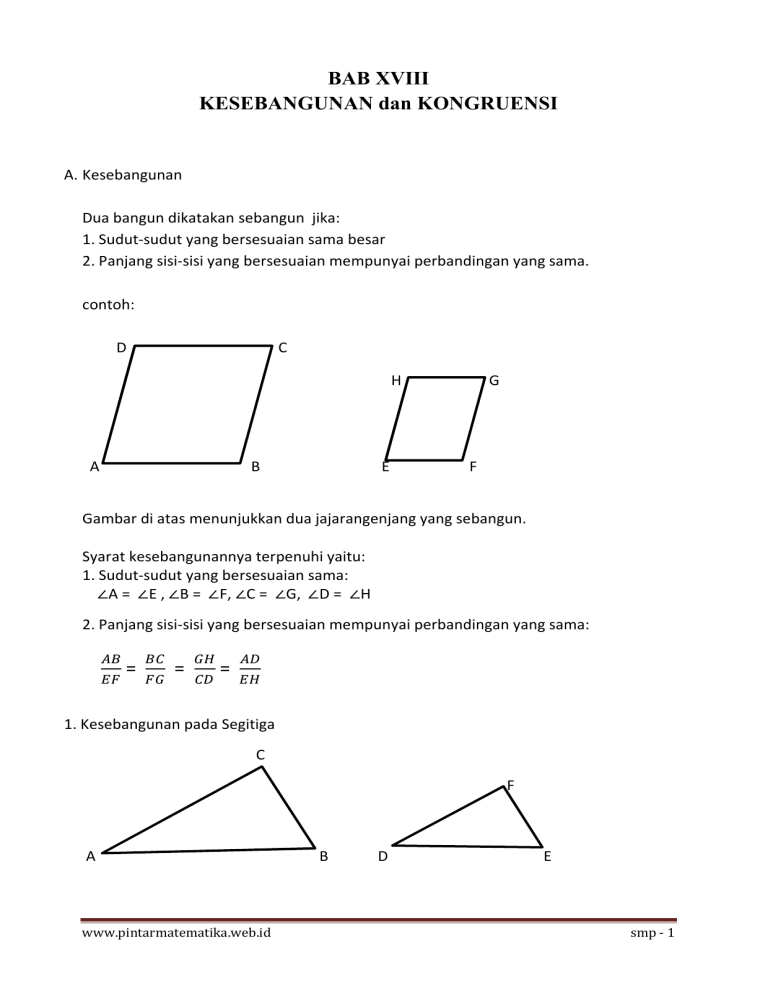
BAB XVIII
KESEBANGUNAN dan KONGRUENSI
A. Kesebangunan
Dua bangun dikatakan sebangun jika:
1. Sudut-sudut yang bersesuaian sama besar
2. Panjang sisi-sisi yang bersesuaian mempunyai perbandingan yang sama.
contoh:
D
C
H
A
B
E
G
F
Gambar di atas menunjukkan dua jajarangenjang yang sebangun.
Syarat kesebangunannya terpenuhi yaitu:
1. Sudut-sudut yang bersesuaian sama:
∠A = ∠E , ∠B = ∠F, ∠C = ∠G, ∠D = ∠H
2. Panjang sisi-sisi yang bersesuaian mempunyai perbandingan yang sama:
=
=
=
1. Kesebangunan pada Segitiga
C
F
A
www.pintarmatematika.web.id
B
D
E
smp - 1
Sudut-sudut yang bersesuaian pada dua segitiga di atas adalah sama:
∠A = ∠D , ∠B = ∠E, ∠C = ∠F
Jika segitiga ABC dan DEF sebangun maka panjang sisi-sisi yang bersesuaian
mempunyai perbandingan yang sama:
=
=
Perbandingan Panjang Sisi Dua Segitiga Sebangun
a. AB sejajar DE :
C
D a
c E
b
d
A
B
Pada segitiga di atas berlaku:
1.
=
=
atau
=
=
2. ∠a = ∠b dan ∠c = ∠d
b. AD tegak lurus BC ( AD ⊥ BC):
C
D
A
www.pintarmatematika.web.id
B
smp - 2
1. ∆ ABC sebangun dengan ∆ ADC maka AC2 = CD x CB atau AC = √
2. ∆ ABC sebangun dengan ∆ ABD maka AB2 = BD x BC atau AB = √
3. ∆ ABD sebangun dengan ∆ ADC maka AD2 = BD x CD atau AD = √
c.
a
b
c
d
f
e
= =
berlaku :
2. Kesebangunan pada segiempat ( trapesium) :
D
C
E
F
A
B
berlaku :
EF =
.
.
B. Kekongruenan
Dua bangun datar dikatakan kongruen jika kedua bangun tersesebut memiliki bentuk
dan ukuran yang sama.
www.pintarmatematika.web.id
smp - 3
Dua segitiga kongruen jika:
1. Dua sisi sama panjang dan sudut apitnya sama besar
(sisi, sudut, sisi)
C
F
A
-
AB = DE
∠A = ∠D
AC = DF
B
D
E
sisi
sudut
sisi
2. Dua sudut sama besar dan sisi yang diapit sama panjang
(sudut, sisi, sudut)
C
A
-
∠A = ∠D
AB = DE
∠B = ∠E
F
B
D
E
sudut
sisi
sudut
www.pintarmatematika.web.id
smp - 4
3. Ketiga sisi sama panjang (sisi,sisi,sisi)
C
A
-
AC = DF
AB = DE
BC = EF
F
B
D
E
sisi
sisi
sisi
www.pintarmatematika.web.id
smp - 5