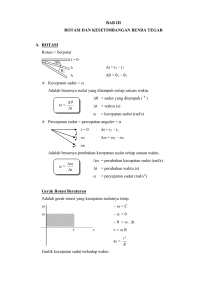
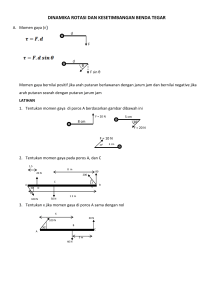
Titik berat benda berbentuk garis dan busur

http//:yohafrinal.wordpress.com
BAB. 6
DINAMIKA ROTASI DAN KESETIMBAGAN BENDA TEGAR
A. MOMEN GAYA DAN MOMEN INERSIA
1. Momen Gaya
Benda hanya dapat mengalami perubahan gerak rotasi jika pada benda tersebut diberi momen gaya,
dengan adanya momen gaya maka benda akan mengalami perubahan kecepatan sudut, sehingga
momen gaya merupakan perkalian silang antara antara posisi (r) dan gaya (F). dimana r = l sin θ
Secara matematis momen gaya dirumuskan sebagai berikut:
𝜏=𝑟𝑥𝐹
atau
𝜏 = −𝐹 𝑙 sin 𝜃
τ = negatif jika berputar berlawanan arah jarum jam
𝜏 = 𝐹 𝑙 sin 𝜃
τ = positif jika berputar searah jarum jam
F
F
l
l
torsi berlawanan arah jarum jam
(negatif)
torsi searah jarum jam
(Positif)
Jika pada benda bekerja lebih dari satu gaya, resultan momen gaya yang bekerja pada benda merupakan
jumlah vector dari setiap momen gaya
𝜏 = ∑(𝑟 𝑥 𝐹)
Catatan
Jika arah rotasi yang ditimbulkan oleh F, searah dengan arah jarum jam maka τ berharga positif.
Jika arah rotasi yang ditimbulkan oleh F, berlawanan arah dengan arah jarum jam maka τ berharga
negatif.
2. Momen Kopel
Momen kopel merupakan pasangan dua buah gaya yang sejajar, sama besar, dan berlawan arah.
Momen kopel (M) adalah perkalian silang antara vector gaya dan vektor jarak antara dua gaya
tersebut
𝑀=𝐹𝑥𝑑
Penentuan arah momen kopel sesuai aturan sekrup (aturan tangan kanan)
Jika arah (M) masuk bidang gambar dianggap positif
Jika arah (M) keluar bidang gambar dianggap negative
Modul Fisika Kelas XI. IPA Kurikulum 2013
1
http//:yohafrinal.wordpress.com
Jika pada sebuah gambar sebuah benda ada beberapa buah kopel sebidang, putaran resultan momen
kopelnya merupakan jumlah aljabar dari setiap momen kopelnya.
𝑀𝑟𝑒𝑠 = ∑ 𝑀
𝑀
𝑑 = |𝐹 |
d = pergeseran titik tangkap gaya
3. Momen Inersia benda titik (partikel)
Kecenderungan benda untuk selalu mempertahankan geraknya
Momen inersia tergantung pada massa dan posisi massa benda ke sumbu putarnya, semakin jauh
posisi massa benda ke pusat rotasinya, maka semakin besar momen inersia benda tersebut.
𝐼 = 𝑚𝑟 2
Momen inersia sebuah benda yang tersusun oleh partikel-partikel dapat ditulis menjadi
𝐼 = ∑ 𝑚𝑛 𝑟𝑛2
𝑛
4. Momen Inersia benda tegar
𝑥2
𝑚
𝑚 𝑥2
𝐼 = ∫ 𝑥 2 ( ) 𝑑𝑥 = ( ) ∫ 𝑥 2 𝑑𝑥
𝑙
𝑙 𝑥1
𝑥1
No
1
Gambar
Nama
Momen Inersia
1
𝑚𝑙 2
12
Batang terhadap sumbu yang
melalui pusat
𝐼=
Batang terhadap sumbu pada
satu ujungnya
1
𝐼 = 𝑚𝑙 2
3
Cincin tipis terhadap sumbu
silinder
𝐼 = 𝑚𝑅 2
l
2
l
3
R
Modul Fisika Kelas XI. IPA Kurikulum 2013
2
http//:yohafrinal.wordpress.com
No
4
Gambar
Nama
R
5
Momen Inersia
Piringan atau cakram titik
terhadap sumbu melalui pusat
𝐼=
1
𝑚𝑅 2
2
Silinder pejal terhadap sumbu
silinder
𝐼=
1
𝑚𝑅 2
2
l
6
Silender berongga terhadap
sumbu melalui titik pusat
R1
R2
7
2R
8
2R
engsel
𝐼=
2
𝑚𝑅 2
5
Bola berongga terhadap sumbu
melalui titik pusat
𝐼=
2
𝑚𝑅 2
3
F2 = 5 N
300
1
𝑚(𝑅12 + 𝑅22 )
2
Bola pejal terhadap sumbu
melalui titik pusat
Uji Kompetensi
1. Jika diketahui panjang batang adalah 1 meter,
maka resultan momen gaya yang bekerja pada
engsel
F1 = 10 N
𝐼=
0,25 m
2. Sebuah pesawat sederhana digunakan untuk
mengangkat beban bermassa 10 kg, jika
panjang batang pengungkit 2 m dan letak
penumpu 0,75 m dari ujung beban, maka gaya
yang dibutuhkan untuk mengangkat beban
adalah …
F3 = 10 N
a.
b.
c.
d.
e.
1,50 Nm
1,25 Nm
1,50 Nm
2,75 Nm
2,90 Nm
Modul Fisika Kelas XI. IPA Kurikulum 2013
a.
b.
c.
d.
e.
30 N
40 N
50 N
60 N
70 N
0,75 m
3
http//:yohafrinal.wordpress.com
3. Sebuah batang panjangnya l, massa m, dan
1
sumbu rotasi terletak pada 3 𝑙 dari ujung kiri
batang dan tegak lurus terhadap batang,
tentukan besarnya momen inersia batang
terhadap sumbu rotasinya…
1
1
a. 𝐼 = 3 𝑚𝑙 2
𝑙
5. Sebuah segitiga siku-siku, panjang sisi
miringnya AC = 50 cm, pada titik sudutnya
ditempatkan partikel bermassa 0,01 kg, sebuah
sumbu putar melalui titik A dan tegak lurus
garis AB, tentukan momen inersianya.
(cos 37 = 0,8 dan sin 37 = 0,6)
C
3
1
a.
b.
c.
d.
e.
b. 𝐼 = 6 𝑚𝑙 2
1
c. 𝐼 = 9 𝑚𝑙
1
l
2
d. 𝐼 = 12 𝑚𝑙
0,1 g.cm2
0,2 g.cm2
0,3 g.cm2
0,4 g.cm2
0,5 g.cm2
2
50 cm
A
370
B
1
e. 𝐼 = 24 𝑚𝑙 2
4. Pada titik sudut sebuah segitiga siku-siku
dengan panjang sisi 3 cm dan 5 cm, ditempat
titik materi dengan massa mA = 5 gram, mB =
10 gram dan mc = 20 gram. Tentukan momen
inersia titik-titik materi tersebut jika sumbu
rotasi di titik A dan tegak lurus bidang ABC.
a. 190 g.cm2
C
2
b. 290 g.cm
c. 390 g.cm2
d. 490 g.cm2
e. 590 g.cm2
5 cm
A
3 cm
B
B. DINAMIKA GERAK ROTASI
Telah diketahui bahwa penyebab gerak translasi adalah gaya dan penyebab gerak rotasi momen gaya,
kedua gerak tersebut dapat diungkapkan menggunakan hukum II Newton, dari keadaan diam diam
sebuah benda bermassa m dapat memiliki percepatan a karena pengaruh F sehingga hubungan tersebut
dapat ditulis dengan F = ma. Demikian juga dari keadaan diam sebuah roda yang memiliki inersia I
dapat memiliki percepatan sudut α karena pengaruh momen gaya F, sehingga secara matematis dapat di
tulis dengan τ = Iα
Modul Fisika Kelas XI. IPA Kurikulum 2013
4
http//:yohafrinal.wordpress.com
Analogi dan hubungan antara persamaan gerak translasi benda tegar sepanjang garis lurus dan gerak
rotasi mengelilingi sumbu rotasi dapat di lihat seperti table
Gerak translasi
Jarak linier
Gerak rotasi
s
Jarak (posisi) sudut
𝑑𝑠
𝑑𝑡
𝑑𝑣
𝑎𝑡 =
𝑑𝑡
Kecepatan linier
𝑣=
Percepatan
tangensial
Kecepatan sudut
Percepatan sudut
Hubungan
Θ
s = θR
𝑑𝜃
𝑑𝑡
𝑑𝜔
𝛼=
𝑑𝑡
v = ωR
𝜔=
a = αR
𝑁
Kelembaman rotasi
benda tegar (momen
inersia)
I
F = ma
Torsi (momen gaya)
τ = Iα
τ=rF
Energi Kinetik
1
𝐸𝑘 = 𝑚𝑣 2
2
Energi kinetik
1
𝐸𝑘 = 𝐼𝜔2
2
-
Momentum linier
p = mv
Momentum sudut
L = Iω
-
Daya
p=Fv
Daya
p = τω
-
Kelembaman
translasi (massa)
m
Gaya
𝐼 = ∑ 𝑚𝑅 2
𝑖=1
Aplikasi Gerak Rotasi
1. Katrol dihubungkan dengan beban
a. Tinjau gaya-gaya pada beban m dengan menggunakan
Hukum II Newton
α
∑ 𝐹 = 𝑚𝑎
b. Tinjauan gaya-gaya pada katrol untuk gerak rotasi
Hukum II Newton untuk gerak rotasi pada katrol
𝑎
∑ 𝜏 = 𝐼𝛼
dengan 𝛼 = 𝑅
𝑎
𝑇𝑅 = 𝐼 𝑅

a
T
𝑚𝑔 − 𝑇 = 𝑚𝑎
T
mg
𝑎
𝑇 = 𝐼 𝑅2
Modul Fisika Kelas XI. IPA Kurikulum 2013
5
http//:yohafrinal.wordpress.com
Dengan mensubsitusi kedua persamaan tersebut diperoleh hubungan sebagai berikut:
𝑎=
𝑚𝑔
𝑚+
𝐼
𝑅2
2. Menggelinding pada bidang horizontal
a. Tinjau gaya-gaya pada benda dengan menggunakan
∑ 𝐹 = 𝑚𝑎
dan
∑𝐹 = 0
𝐹 − 𝑓𝑠 = 𝑚𝑎
dan
𝑁 − 𝑚𝑔 = 0
N
α
F
Fs
b. Tinjauan gaya-gaya pada katrol untuk gerak rotasi
Hukum II Newton untuk gerak rotasi pada katrol
𝑎
∑ 𝜏 = 𝐼𝛼
dengan 𝛼 = 𝑅
𝑎
𝑎

𝑓𝑠 𝑅 = 𝐼 𝑅
mg
𝑓𝑠 = 𝐼 𝑅2
Dengan mensubsitusi kedua persamaan tersebut diperoleh hubungan sebagai berikut:
𝑎=
𝐹
𝑚+
𝐼
𝑅2
3. Menggelinding pada bidang miring
N
a. Tinjau gaya-gaya pada benda dengan menggunakan
fs
∑ 𝐹 = 𝑚𝑎
dan
𝑚𝑔 sin 𝜃 − 𝑓𝑠 = 𝑚𝑎
∑𝐹 = 0
dan
𝑎

mg con θ
𝑁 − 𝑚𝑔 𝑐𝑜𝑠 𝜃 = 0
b. Tinjauan gaya-gaya pada katrol untuk gerak rotasi
Hukum II Newton untuk gerak rotasi pada katrol
𝑎
∑ 𝜏 = 𝐼𝛼
dengan 𝛼 = 𝑅
𝑓𝑠 𝑅 = 𝐼 𝑅
mg sin θ
mg
θ
𝑎
𝑓𝑠 = 𝐼 𝑅2
Dengan mensubsitusi kedua persamaan tersebut diperoleh hubungan sebagai berikut:
𝑎=
𝑚𝑔 sin 𝜃
𝐼
𝑚+ 2
𝑅
Modul Fisika Kelas XI. IPA Kurikulum 2013
6
http//:yohafrinal.wordpress.com
4. Energi Kinetik dan Hukum kekekalan energi kinetik
1
1
𝐸𝑘 = 2 𝑚𝑣 2 + 2 𝐼𝜔2
dan
𝐸𝑘1 + 𝐸𝑝1 = 𝐸𝑘2 + 𝐸𝑝2
Uji Kompetensi
1. Tentukan besarnya momentum sudut dari
sebuah piringan CD yang massanya 60 gram,
jari-jarinya 5 cm ketika sedang berotasi dengan
sumbu putar melalui titik pusat massa dan
tegak lurus piringan dengan kecepatan sudut 10
rad/s. …
a. 5 kgm2s-2
b. 5 kgm2s-2
c. 5 kgm2s-2
d. 5 kgm2s-2
e. 5 kgm2s-2
2. Diketahui massa katrol 1 kg, jari-jari 5 cm,
massa beban m1 =0,4 kg, dan m2 = 0,6 kg
tentukan percepatan linier system
a. 1/3 m/s2
b. 2/3 m/s2
c. 4/3 m/s2
d. 5/3 m/s2
e. 7/3 m/s2
m1
m2
4. Silinder pejal bermassa 20 kg dan jari-jari 10
cm, didorong dengan gaya 100 N pada bidang
datar yang kasar, maka percepatan yang
dialami benda adalah …
a. 3,33 m/s2
b. 4,33 m/s2
c. 5,33 m/s2
d. 6,33 m/s2
e. 7,33 m/s2
5. Sebuah cincin tipis bermassa 20 gram
menggelinding tanpa slip pada sebuah bidang
miring dengan sudut 300 terhadap bidang
horizontal dengan kecepatan awal 2 m/s,
tentukan percepatan dan kecepatan cincin
setelah menempuh jarak 1 m …
a. ..
b. ..
c. ..
d. ..
e. ..
3. Sebuah bola pejal dapat melakukan gerakan
translasi dan rotasi pada sebuah bidang miring
yang memiliki ketinggian 1 m, jika g = 10 m/s2
. tentukan kecepatannya pada kaki bidan
miring.
a. 3,0 m/s
b. 3,3 m/s
c. 3,6 m/s
d. 4,3 m/s
e. 4,6 m/s
Modul Fisika Kelas XI. IPA Kurikulum 2013
7
http//:yohafrinal.wordpress.com
C. KESETIMBANGAN BENDA TEGAR
Menurup hukum I Newton, jika resultan gaya-gaya sama dengan nol, percepatan partikel sama dengan
nol, maka benda dalam keadaan diam atau bergerak lurus beraturan, dan partikel dalam keadaan diam
dikatakan mengalami kesetimbangan statis, sedangkan patikel dalam kedaan bergerak dengan kecepatan
tetap mengalami kesetimbangan dinamis. (∑ 𝐹 = 0)
1. Syarat kesetimbangan benda tegar translasi
∑ 𝐹𝑥 = 0 ; ∑ 𝐹𝑦 = 0; ∑ 𝐹𝑧 = 0
2. Syarat kesetimbangan benda tegar rotasi
∑ 𝜏𝑥 = 0 ; ∑ 𝜏𝑦 = 0; ∑ 𝜏𝑧 = 0
salah satu contoh kesetimbangan benda tegar translasi, dan cara penyelesaian persoalannya, Perhatikan
gambar dibawah kita dapat menentukan tegangan tali (T1 dan T2)
∑ 𝐹𝑥 = 0 dan
600
∑ 𝐹𝑦 = 0
T1
Semua gaya yang bekerja pada system harus diproyeksikan pada
Sumbu-x dan sumbu-y
300
T2
T1 sin 60
T2 sin 30
m=10 kg
T1 cos 60
T2 cos 30
w=mg
1
1
∑ 𝐹𝑥 = 0  𝑇2 cos 30 − 𝑇1 cos 60 = 0  𝑇2 ( √3) − 𝑇1 ( ) = 0 …. (1)
2
2
1
1
∑ 𝐹𝑦 = 0  𝑇1 sin 60 + 𝑇2 sin 30 − 𝑤 = 0  𝑇1 ( √3) + 𝑇2 ( ) − 100 = 0 …. (2)
2
2
Subsitusikan persamaan (1) dan persamaan (2)
1
1
1
1

Pers (1)
𝑇2 (2 √3) − 𝑇1 (2) = 0
Pers (2)
𝑇1 (2 √3) + 𝑇2 (2) − 100 = 0 
Modul Fisika Kelas XI. IPA Kurikulum 2013
𝑇2 (√3) − 𝑇1 = 0
 𝑇2 (√3) = 𝑇1
𝑇1 (√3) + 𝑇2 − 200 = 0
8
http//:yohafrinal.wordpress.com
𝑇2 (√3)(√3) + 𝑇2 − 200 = 0
𝑇2 3 + 𝑇2 − 200 = 0
4𝑇2 = 200
𝑇2 = 50 𝑁
Untuk menentukan T1 yaitu dengan menggunakan salah satu persamaan
Pers (1)
𝑇2 (√3) = 𝑇1 
𝑇1 = 50√3
fB
Berikut contoh kesetimbangan benda tegar translasi dan rotasi
pada batang homogen, lantai dan dinding kasar, datang tepat akan meluncur.
NB
B
Syarat kesetimbangan benda tegar translasi pada sumbu xy
∑ 𝐹𝑥 = 0
∑ 𝐹𝑦 = 0
𝑓𝐴 − 𝑁𝐵 = 0 … (1)
𝑓𝐵 + 𝑁𝐴 − 𝑤 = 0 …. (2)
l
NA
Syarat kesetimbangan benda tegar rotasi dengan tinjauan pusat
Momen gaya di A
w
α
fA
A
∑ 𝜏𝐴 = 0
1
𝑤. 2 𝑙 cos 𝛼 − 𝑁𝐵 . 𝑙 sin 𝛼 − 𝑓𝐵 . 𝑙 cos 𝛼 = 0 …(3)
Dengan mensubsitusikan ketiga persamaan dapat ditentukan besarnya gaya yang bekerja pada tiap titik
pada batang homogen tersebut.
D. TITIK BERAT BENDA
Titik berat adalah titik tangkap gaya berat sebuah benda
Untuk benda bidang :
untuk benda bermassa
𝑦0 =
∑ 𝐴𝑦
∑𝐴
Modul Fisika Kelas XI. IPA Kurikulum 2013
𝑦0 =
∑ 𝑤𝑦
∑𝑤
9
http//:yohafrinal.wordpress.com
Titik berat benda berbentuk garis dan busur
Gambar
Nama
y0
A
Z
A
Hubungan
Garis lurus
1
𝑦0 = 𝐴𝐵
2
Z = tengah tengan AB
𝐴𝐵 = 𝑡𝑎𝑙𝑖 𝑏𝑢𝑠𝑢𝑟 𝐴𝐵
Busur lingkaran
𝐴𝐵
𝑦0 = 𝑅
̂
𝐴𝐵
𝐴𝐵 = ̂
𝑏𝑢𝑠𝑢𝑟 𝐴𝐵
R = Jari-jari
B
Z
y0
Letak titik berat
B
R
M
Busur setengah
lingkaran
z
y0
𝑦0 =
2𝑅
3𝜋
R = Jari-jari lingkaran
M
Titik berat benda berbentuk bidang himogen
Gambar
A
z
R
Nama
B
Juring lingkaran
y0
Letak titik berat
𝑦0 =
Hubungan
1 𝐴𝐵
𝑅
̂
2 𝐴𝐵
𝐴𝐵 = 𝑡𝑎𝑙𝑖 𝑏𝑢𝑠𝑢𝑟 𝐴𝐵
̂ = 𝑏𝑢𝑠𝑢𝑟 𝐴𝐵
𝐴𝐵
R = Jari-jari
4𝑅
3𝜋
R = Jari-jari lingkaran
M
Setengah lingkaran
z
y0
𝑦0 =
M
Titik berat benda berbentuk selimut
Gambar
Nama
Selimut setengah bola
z
y0
Letak titik berat
𝑦0 =
1
𝑅
2
Hubungan
R = Jari-jari bola
R
M
Selimut limas
y0
Modul Fisika Kelas XI. IPA Kurikulum 2013
1
𝑦0 = 𝑡
3
t = tinggi limas
10
http//:yohafrinal.wordpress.com
Gambar
Nama
Letak titik berat
1
𝑦0 = 𝑡
3
Selimut kerucut
y0
Hubungan
t = tinggi kerucut
Titik berat benda berbentuk pejal homogeny
Gambar
Nama
Letak titik berat
Setengah bola pejal
z
y0
𝑦0 =
3
𝑅
8
Hubungan
R = jari-jari bola
R
M
Limas Pejal
1
𝑦0 = 𝑡
4
t = tinggi limas
Kerucut pejal
1
𝑦0 = 𝑡
4
t = tinggi kerucut
y0
y0
Uji Kompetensi
1. Sebuah benda dengan berat 480 N digantung
dalam keadaan setimbang, seperti pada gambar,
maka besar tegangan tali T1 adalah
a.
b.
c.
d.
e.
500 N
480 N
240 N
120 N
80 N
530
370
T2
T1
w
2. Sebuah tangga AB homogen panjangnya 5 m
dan beratnya 100 N, ujung A terletak pada
lantai dan ujung B pada dinding, ujung A
berjarak 3 meter dari dinding, koefisien statis A
dan B sama yaitu 0,5, maka jarak terjauh yang
dapat dicapai seseorang yang memanjat tangga
dengan berat 500 N adalah (tangga belum
tergelincir)
B
a. 3,5 m
b. 3,6 m
c. 3,7 m
d. 3,8 m
e. 3,9 m
A
Modul Fisika Kelas XI. IPA Kurikulum 2013
11
http//:yohafrinal.wordpress.com
Modul Fisika Kelas XI. IPA Kurikulum 2013
12