Materi Kalkulus 2 : 4 SKS

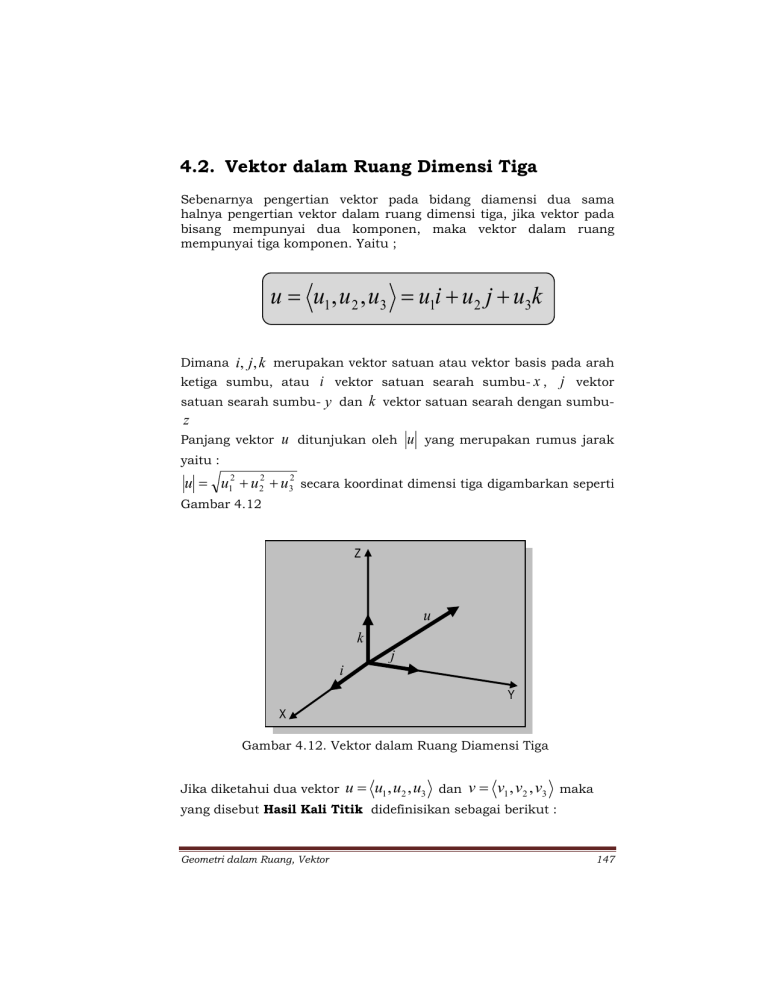
4.2. Vektor dalam Ruang Dimensi Tiga
Sebenarnya pengertian vektor pada bidang diamensi dua sama
halnya pengertian vektor dalam ruang dimensi tiga, jika vektor pada
bisang mempunyai dua komponen, maka vektor dalam ruang
mempunyai tiga komponen. Yaitu ;
u  u1 , u2 , u3  u1i  u2 j  u3k
Dimana i, j , k merupakan vektor satuan atau vektor basis pada arah
ketiga sumbu, atau i vektor satuan searah sumbu- x , j vektor
satuan searah sumbu- y dan
k vektor satuan searah dengan sumbu-
z
Panjang vektor
u ditunjukan oleh u yang merupakan rumus jarak
yaitu :
u  u12  u 22  u32 secara koordinat dimensi tiga digambarkan seperti
Gambar 4.12
Z
u
k
j
i
Y
X
Gambar 4.12. Vektor dalam Ruang Diamensi Tiga
Jika diketahui dua vektor
u  u1 , u2 , u3 dan v  v1 , v2 , v3 maka
yang disebut Hasil Kali Titik didefinisikan sebagai berikut :
Geometri dalam Ruang, Vektor
147
u  v  u1v1  u2 v2  u3v3
u  v  u v Cos
Contoh 4.13 :
Tentukan
sudut
ABC
C  5,3,2 dan Gamarkan
jika
A  1,2,3 ,
B  2,4,6
dan
Penyelesaian 4.13 :
Jika digamabar sebagai berikut :
A  1,2,3

B  2,4,6  
.
 C  5,3,2 
Misalkan vektor
u adalah vektor yang titik asalnya di titik B dan titik

ujungnya di titik A atau vektor BA dan vektor
v adalah vektor yang

titik asalnya di titik B dan titik ujungnya di titik C atau vektor BC ,
maka vektor u dan v dapat ditentukan sebagai berikut.

.
BA  u  (1  2), (2  4), (3  (6))   1,6,9
.
BC  v  (5  2), (3  4), (2  (6))  3,7,8


Cos 
uv
uv
Geometri dalam Ruang, Vektor
148
Cos 
 (1)
(1)(3)  (6)(7)  (9)(8)
2
 (6) 2  9 2
 3
2
 (7) 2  8 2
 3  42  72
Cos 
 1  36  81
Cos 
111
 118  122 
Cos 
111
10,86311,045
Cos 
111
 0,925
119,9818
9  49  64


  22,310
4.2.1. Sudut dan Kosinus Arah
Jika diketahui suatu vektor yaitu vektor u , sudut yang tak nol antara
vektor u dengan vektor satuan yang searah dengan sumbu koordinat
yaitu i , j dan k disebut sudut-sudut arah vektor u , jika sudutsudut tersebut dilambangkan dengan ,  dan , jika vektor
u
u  u1i  u 2 j  u3 k , maka sudut-sudut itu
dinyatakan sebagai Cos , Cos dan Cos dimana secara rumus
dinyatakan
sebagai
diberikan :
Cos 
u
ui
 1
ui
u
Cos 
u
uj
 2
u j
u
Cos 
u
uk
 3
uk
u
Berlaku juga
Cos 2  Cos 2   Cos 2  1 seperti Gambar 4.13
Geometri dalam Ruang, Vektor
149
Z
u
k
j
i
Y
X
Gambar 4.13. Sudut-Sudut Arah Vektor
Contoh 4.14 :
Diketahui vektor u  2i  3 j  4k tentukan sudut-sudut arah untuk
vektor u
Penyelesaian 4.14 :
Diketahui vektor u  2i  3 j  4k , maka
u  2 2  32  4 2  4  9  16  29



Cos 
Cos 
Cos 
2
29
3
29
4
29
Geometri dalam Ruang, Vektor
150
4.2.2. Bidang Dibentuk Oleh Vektor
Untuk melukiskan sebuah bidang ada beberapa cara, salah satunya
dengan menggunakan bahasa vektor atau dengan menggunakan
bantuan vektor, misalkan
nol dan
n  A, B, C adalah sebuah vektor yang tak
P1 x1 , y1 , z1  adalah titik tetap, jika koordinat Px, y, z  yang
memenuhi persamaan

P1 P n  0 adalah sebuah bidang yang melalui
P1 dan tegak lurus n , seperti pada Gambar 4.14
n  A, B, C
P1P  x  x1 , y  y1 , z  z1

P1 x1 , y1 , z1 

Px, y, z 
Bidang
Gambar 4.14. Bidang Melalui titik P1
karena vektor
n  A, B, C

tegak lurus dengan vektor
P1 P atau

P1 P n  0 atau :


x  x1 , y  y1 , z  z1  A, B, C  0
Ax  x1   B y  y1   Cz  z1   0
Sehingga secara umum jika diketahui sebuah vektor
yang tegak lurus pada sebuah bidang di titik
persamaan bidang dapat ditentukan yaitu :
n  A, B, C
P1 x1 , y1 , z1  , maka
Ax  x1   B y  y1   C z  z1   0
Geometri dalam Ruang, Vektor
151
Contoh 4.15 :
Tentukan persamaan bidang yang melalui titik
lurus dengan vektor
P2,4,3 dan tegak
n  4,3,6
Penyelesaian 4.15 :
P2,4,3 sehingga didapat nilai x1  2 , y1  4 , dan
z1  3 serta vektor n  4,3,6 sehingga didapat nilai A  4 , B  3 ,
dan C  6 , karena rumus untuk menentukan persamaan bidang
adalah Ax  x1   B y  y1   C z  z1   0 , maka :
 Ax  x1   B y  y1   C z  z1   0
 4x  2  3 y  4  6z  3  0
 4 x  8  3 y  12  6 z  18  0
 4 x  3 y  6 z  38
Diketahui titik
Contoh 4.16 :
Tentukan persamaan bidang yang melalui titik
P 4,2,3 dan tegak
lurus dengan vektor n  2i  6 j  4k
Penyelesaian 4.16 :
P 4,2,3 sehingga didapat nilai x1  4 , y1  2 ,
dan z1  3 serta vektor n  2i  6 j  4k sehingga didapat nilai
A  2 , B  6 , dan C  4 , karena rumus untuk menentukan
persamaan bidang adalah Ax  x1   B y  y1   C z  z1   0 , maka :
 Ax  x1   B y  y1   C z  z1   0
 2x   4  6 y  2  4z   3  0
 2 x  8  6 y  12  4 z  12  0
 2 x  6 y  4 z  16
Diketahui titik
Geometri dalam Ruang, Vektor
152
4.2.3. Jarak Titik Ke Bidang
Px0 , y0 , z 0  dan sebuah bidang yang
mempunyai persamaan Ax  By  Cz  D , maka jika L menyatakan
Jika diberikan suatu titik
suatu jarak dari titik tertentu ke suatu bidang, maka
dinyatakan dengan rumus :
L
jarak itu
Ax0  By0  Cz0  D
A2  B 2  C 2
Pandang sebuah bidang seperti Gambar 4.15
n  A, B, C

x0 , y0 , z0 
L  m
x1 , y1 , z1 
Gambar 4.15. Jarak Titik ke Bidang
Misalkan titik
x1 , y1 , z1 
terletak pada bidang datar, andaikan
m  x0  x1 , y0  y1 , z 0  z1  adalah vektor dari titik
titik x0 , y 0 , z 0  .
x1 , y1 , z1 
ke
n  A, B, C adalah vektor yang tegak lurus terhadap bidang yang
diberikan, maka bilangan L adalah proyeksi vektor m pada n , maka
diperoleh :

L  m cos  

L
mn
n
Ax0  x1   B y 0  y1   C z 0  z1 
A2  B 2  C 2
Geometri dalam Ruang, Vektor
153

L

L

L
Ax 0  Ax1  By 0  By1  Cz 0  Cz1
A2  B 2  C 2
Ax 0  By 0  Cz 0   Ax1  By1  Cz1 
A2  B 2  C 2
Ax 0  By 0  Cz 0  D
karena titik
A2  B 2  C 2
bidang, maka Ax1  By1  Cz1  D
x1 , y1 , z1 
terletak pada
Contoh 4.17 :
Tentukan jarak titik
P 4,2,3 ke bidang 3x  4 y  5z  9
Penyelesaian 4.17 :
A  3 , B  4 ,
C  5 , dan D  9 , dari titik P 4,2,3 diketahui nilai x1  4 ,
y1  2 , dan z1  3 , maka jarak titik P 4,2,3 ke bidang
3x  4 y  5z  9 adalah :
Ax 0  By 0  Cz 0  D
 L
A2  B 2  C 2
(3)(4)  (4)(2)  (5)(3)  9
 L
3 2  (4) 2  5 2
Dari bidang datar 3x  4 y  5z  9 diketahui nilai

L

L
 12  8  15  9
9  16  25
41
50
Geometri dalam Ruang, Vektor
154
4.2.4. Dua Bidang Sejajar
Diketahui ada dua buah bidang yang masing-masing mempunyai
persamaan A1 x  B1 y  C1 z  D1 dan A2 x  B2 y  C2 z  D2 kedua
bidang dikatakan sejajar jika :
A1  A2 , B1  B2 , C1  C2 dan D1  D2 ,
Catatan :
 Suatu
Pa, b, c  dikatakan terletak pada
A1 x  B1 y  C1 z  D1 jika A1 a   B1 b  C1 c   D1
Pa, b, c  dikatakan terletak pada
 Suatu titik
A2 x  B2 y  C2 z  D2 jika A2 a   B2 b  C2 c   D2
titik
bidang
bidang
Contoh 4.18 :
3x  4 y  2 z  8 ,
tentukan sebuah bidang yang melalui titik P2,2,2 dan sejajar
dengan bidang 3x  4 y  2 z  8
Diketahui
sebuah
bidang
dengan
persamaan
Penyelesaian 4.18 :
3x  4 y  2 z  8 , maka bidang
3x  4 y  2 z  8
bidang
adalah
Diketahui bidang dengan persamaan
yang
sejajar
dengan
3x  4 y  2 z  D2 , karena bidang yang sejajar dengan bidang
3x  4 y  2 z  8 melalui titik P2,2,2 , maka diperoleh nilai D2 yaitu
 3x  4 y  2 z  D2
 32  42  22  D2
 6  8  4  D2
 D2  10
Sehingga
persamaan
bidang
yang
sejajar
dengan
bidang
3x  4 y  2 z  8 dan melalui titik P2,2,2 adalah 3x  4 y  2 z  10
Geometri dalam Ruang, Vektor
155
Contoh 4.19 :
Diketahui dua bidang sejajar yaitu bidang I :
bidang II :
itu
5x  3 y  4 z  12 , dan
5x  3 y  4 z  4 , berapa jarak kedua bidang yang sejajar
Penyelesaian 4.19 :
Jika kita ilustrasikan dengan gambar, sebagai berikut :
Bid I : 5x  3 y  4 z  12
L
Pa, b, c  
Bid II : 5x  3 y  4 z  4
Untuk menentukan jarak kedua bidang itu atau L , maka kita harus
menentukan sebuah titik P a, b, c yang terletak pada bidang II,
caranya adalah :
 5x  3 y  4 z  4
jika kita beri nilai x  1 dan y  1 , maka
diperoleh :
 5 1  3 1  4z  4


 
 5  3  4z  4
 8  4z  4
  4 z  4
 z 1
Sehingga diperoleh titik yang terletak pada bidang


5x  3 y  4 z  4
yaitu P 1,1,1 , dan untuk mengetahui jarak kedua bidang kita
gunakan jarak sebuah titik ke bidang, dalam hal ini kita tentukan
jaraka titik P 1,1,1 ke bidang I yaitu 5x  3 y  4 z  12 dengan


menggunakan rumus :
L
Geometri dalam Ruang, Vektor
Ax 0  By 0  Cz 0  D
A2  B 2  C 2
156

L

L

L

L

L
Ax 0  By 0  Cz 0  D
A2  B 2  C 2
51  31  41  12
5 2  3 2   4
2
5  3  4  12
25  9  16
8
50
8
50
Sehingga diperoleh jarak bidang I :
5x  3 y  4 z  4 adalah
5x  3 y  4 z  12 ke bidang II :
8
50
4.2.5. Dua Bidang Tegak Lurus
Jika diketahui dua bidang yaitu bidang I
bidang II A2 x  B2 y  C2 z 
lurus seperti Gambar 4.16
A1 x  B1 y  C1 z  D1 dan
D2 , dua bidang tersebut dikatakan tegak
m  A2 , B2 , C2
A1 x  B1 y  C1 z  D1
n  A1 , B1 , C1
A2 x  B2 y  C2 z  D2
Gambar 4.16 : Bidang Saling Tegak Lurus
Geometri dalam Ruang, Vektor
157
n  A1 , B1 , C1
Dari Gambar 4.16 dapat diketahui, bahwa vektor
adalah vektor yang tegak lurus bidang I
sedangkan vektor
m  A2 , B2 , C2
A1 x  B1 y  C1 z  D1 ,
adalah vektor yang tegak lurus
A2 x  B2 y  C2 z  D2 , bidang I dikatakan tegak lurus
n  A1 , B1 , C1
II jika vektor
tegak lurus vektor
bidang II
bidang
m  A2 , B2 , C2 , dua buah vektor
m  A2 , B2 , C2
dikatakan
tegak
n  A1 , B1 , C1
lurus
jika
dan
nm  0
vektor
atau
A1 A2  B1 B2  C1C2  0
Contoh 4.20 :
Diketahui dua buah bidang yaitu bidang I dengan persamaan
2 x  3 y  2 z  7 dan bidang II dengan persamaan x  2 y  2 z  9
apakah kedua bidang tersebut tegak lurus ?
Penyelesaian 4.20 :
Diketahui bidang I 2 x  3 y  2 z  7 maka vektor yang tegak lurus
bidang I adalah
n  2,3,2 , bidang II x  2 y  2 z  9 maka vektor
m  1,2,2 , dua bidang tersebut
dikatakan saling tegak lurus jika n  m  0 , maka :
 nm  0
 A1 A2  B1 B2  C1C2  0
 21  3 2  22  0
 264  0
 00
Karena n  m  0 artinya vektor n  2,3,2 saling tegak lurus dengan
yang tegak lurus bidang II adalah
m  1,2,2 , akibatnya bidang I 2 x  3 y  2 z  7 tegak lurus
bidang II x  2 y  2 z  9
vektor
Geometri dalam Ruang, Vektor
158
Contoh 4.20 :
Diketahui dua buah bidang yaitu bidang I dengan persamaan
3x  4 y  z  9 dan bidang II dengan persamaan  2 x  by  2 z  12
tentukan nilai
b agar kedua bidang itu tegak lurus
Penyelesaian 4.20 :
Diketahui bidang I 3x  4 y  z  9 maka vektor yang tegak lurus
bidang I adalah
n  3,4,1 dan bidang II  2 x  by  2 z  12 maka
vektor yang tegak lurus bidang II adalah
m   2, b,2 , agar kedua
bidang itu tegak lurus, maka haruslah kedua vektor
n  3,4,1 dan
m   2, b,2 juga harus tegak lurus, vektor n  3,4,1 tegak lurus
m   2, b,2 jika n  m  0
 nm  0
 A1 A2  B1 B2  C1C2  0
 3 2   4b  12  0
  6  4b  2  0
  4  4b  0
  4b  4
 b  1
Sehingga agar bidang I 3x  4 y  z  9 tegak lurus bidang II
 2 x  by  2 z  12 , maka nilai b  1
vektor
Geometri dalam Ruang, Vektor
159
4.2.6. Soal-Soal Latihan
A.
Untuk tiap pasangan titik
sketsa ruas garis berarah
dalam bentuk ai  bj  ck
P dan P2 dibawah ini, berikan
1

P1 P2 dan kemudian tulis vektornya
P1 1,2,3 dan P2 4,5,1
2. P1  1,3,3 dan P2  2,4,1
3. P1 0,2,0 dan P2 1,1,1
4. P1  2,1,3 dan P2  4,0,2
1.
B.
Tentukan sudut antara vektor
m dan vektor n di bawah ini
1. m  4,3,2 dan n   1,2,5
2.
m  2,4,1 dan n  2,2,3
m  1,3,3 dan n  1,2,1
4. m  2i  3 j  5k dan n  i  j  k
3.
C.
Tentukan Persamaan Bidang yang melalui titik P dan tegak
lurus vektor n
P1,1,5 dan n  2i  2 j  3k
2. P2,1,3 dan n  3i  2 j  k
3. P1,1,1 dan n  i  4 j  2k
4. P3,1,5 dan n  2i  3 j  2k
1.
D.
Tentukan Persamaan Bidang yang Melalui titik P dan Sejajar
dengan bidang Ax  By  Cz  D
P1,1,1 dan bidang  2 x  4 y  2 z  3
2. P 1,2,3 dan bidang 2 x  4 y  z  6
3. P 4,1,2 dan bidang 2 x  3 y  4 z  0
1.
E.
Tentukan Jarak Titik P ke Bidang Ax  By  Cz  D
P1,1,2 dan bidang x  3 y  z  7
2. P2,6,3 dan bidang  3x  2 y  z  9
1.
F.
Tentukan Jarak Bidang-Bidang Sejajar Berikut
1.  3x  2 y  z  9 dan bidang 6 x  4 y  2 z  19
2. 5x  3 y  2 z  5 dan bidang  5x  3 y  2 z  7
Geometri dalam Ruang, Vektor
160
4.3. Hasil Kali Silang (Cross Product)
Sudah kita ketahui bahwa hasilkali titik dari dua buah vektor
u  u1 , u 2 , u3 dan vektor v  v1 , v2 , v3 adalah sebuah scalar yaitu
melalui rumus :
u  v  u1v1  u2 v2  u3v3
Lain halnya dengan hasilkali silang (cross product) yang menghasilkan
sebuah vektor, jika diketahui dua buah vektor
v  v1 , v2 , v3
u  u1 , u 2 , u3
dan
maka yang disebut hasil kali silang dirumuskan
sebagai berikut :
uxv  u 2 v3  u 3 v2 , u 3 v1  u1v3 , u1v2  u 2 v1
Untuk memperlancar pembahasan hasilkali silang, kita ingat kembali
cara menghitung Determinan, misalnya :
1. Determinan 2x2
Misal diketahui determinan A dengan orde 2x2 yaitu :
A
a b
 ad  bc
c d
2. Determinan 3x3
Misalkan diketahui determinan A dengan orde 3x3 yaitu :
a1
A  b1
c1
a2
b2
c2
a1
 a1 b1
c1
 a1
b2
c2
a3
b3
c3
a2
b2
c2
a3
a1
b3  a2 b1
c3
c1
a2
b2
c2
a3
a1
b3  a3 b1
c3
c1
a2
b2
c2
a3
b3
c3
b3
b b
b b
 a 2 1 3  a3 1 2
c3
c1 c3
c1 c2
Geometri dalam Ruang, Vektor
161
Sehingga jika kita identikan dimana
u  u1 , u 2 , u3 dan
v  v1 , v2 , v3 maka :
i
uxv  u1
v1
j
u2
v2
k
u
u3  2
v2
v3
u3
u u3
u u2
i 1
j 1
k
v3
v1 v3
v1 v2
 u 2 v3  u3 v2 i  u1v3  u3 v1  j  u1v2  u 2 v1 k
 u 2 v3  u3 v2 i  u3 v1  u1v3  j  u1v2  u 2 v1 k
uxv  u2v3  u3v2 , u3v1  u1v3 , u1v2  u2v1
Jika kita menukar uxv menjadi vxu maka komponen vektor u
menempati baris ke tiga dan komponen vektor v menempati baris ke
dua, yaitu :
i
vxu  v1
u1
j
v2
u2
k
v
v3  2
u2
u3
v3
v v3
v v2
i 1
j 1
k
u3
u1 u 3
u1 u 2
 v2 u3  v3u 2 i  v1u3  v3u1  j  v1u 2  v2 u1 k
 v2 u3  v3u 2 i  v3u1  v1u3  j  v1u 2  v2 u1 k
vxu  v2 u3  v3u 2 , v3u1  v1u3 , v1u 2  v2 u1
Contoh 4.21 :
Misalkan
u  1,2,1 dan v   2,4,1 tentukan u  v dan v  u
Penyelesaian 4.21 :

i
j
k
u  v  1  2 1
2 4
1
Geometri dalam Ruang, Vektor
162

 2 1
1 1
1 2
i
j
k
4
1
2 1
2 4
 (2)(1)  (4)(1)i  (1)(1)  (2)(1) j  (1)(4)  (2)(2)k
  2  4i  1  2 j  4  4k
u  v  2i  j  0k

i
j
k
vu   2 4
1
1  2 1

4
1
2 1
2 4
i
j
k
 2 1
1 1
1 2
 (4)(1)  (2)(1)i  (2)(1)  (1)(1) j  (2)(2)  (1)(4)k
  4  2i  2  1 j  4  4k
v  u  2i  j  0k
4.3.1. Tafsiran Geometri u x v
Arti dari hasil kali silang juga perlu digambarkan secara geometri
untuk memperjelas.
Teorema A :
Andaikan u dan v vektor-vektor dalam ruang dimensi tiga
dan  sudut antara mereka, maka :
1.
u  uxv   0  v  uxv  berarti uxv tegak lurus terhadap u
dan v
2. u, v dan uxv membentuk suatu system tangan kanan
rangkap tiga
3.
uxv  u v sin 
Geometri dalam Ruang, Vektor
163
Bukti :
Misalkan diketahui dua buah vektor yaitu
v  v1 , v2 , v3
u  u1 , u 2 , u3
dan
maka sesuai dengan rumus hasilkali silang didapat
uxv  u2v3  u3v2 , u3v1  u1v3 , u1v2  u2v1 , sehingga diperoleh :
u 
uxv 
 u1 u 2 v3  u3 v2   u 2 u3 v1  u1v3   u3 u1v2  u 2 v1 
 u1u 2 v3  u1u3 v2  u 2 u3 v1  u 2 u1v3  u3u1v2  u3u 2 v1
 u1u2 v3  u2u1v3  u1u3v2  u3u1v2  u2 u3v1  u3u2 v1
 u1u 2 v3  u1u 2 v3  u1u3 v2  u1u3 v2  u 2 u3 v1  u 2 u3 v1
u  uxv   0
Artinya vektor
uxv tegak lurus terhadap vektor u
Teorema B :
Dua vektor u dan v dalam ruang dimensi tiga adalah sejajar
jika dan hanya jika u x v = 0
Penerapan dari hasil kali silang kedua vector salah satunya adalah
untuk menentukan persamaan bidang yang melalui tiga titik yang
tidak segaris.
Misalkan diketahui tiga titik yaitu
Aa1 , a2 , a3  , Bb1 , b2 , b3  dan
C c1 , c2 , c3  , dari ketiga titik tersebut dapat diketahui dua buah

vektor
yaitu
vektor
AB  b1  a1 , b2  a2 , b3  a3
dan
vektor

AC  c1  a1 , c2  a2 , c3  a3 .
     

 

Aa1 , a2 , a3  dan tegak lurus bidang yang memuat titik Aa1 , a2 , a3  ,
Vektor  AB    AC   pi  qj  rk adalah vektor yang melalui titik
Bb1 , b2 , b3  dan C c1 , c2 , c3  , maka bidang yang memuat tiga titik
Aa1 , a2 , a3  , Bb1 , b2 , b3  dan C c1 , c2 , c3  mempunyai persamaan :
px  a1   q y  a2   r z  a3   0
Geometri dalam Ruang, Vektor
164
Contoh 4.22 :
Tentukan persamaan bidang yang melalui tiga titik
P2 4,1,2 dan titik P3  2,3,0
P1 1,2,3 , titik
Penyelesaian 4.22 :
Misalkan
vector
menentukan vector

  
u  P2 P1 dan
  
v  P2 P3 sehingga
kita
dapat
u dan vector v yaitu :
  
u  P2 P1  1  4,  2  1, 3  (2)   3,3,5
  
u  P2 P1  3i  3 j  5k

  
v  P2 P3   2  4,  3  1), 0  (2)   6,4,2
  
v  P2 P3  6i  4 j  2k
Diperoleh :
i
j k
uxv   3  3 5
6 4 2
3 5
3 5
3 3
i
j
k
4 2
6 2
6 4
 (3)(2)  (4)(5)i  (3)(2)  (6)(5) j 
(3)(4)  (6)(3)k
  6  20i   6  30 j  12  18k
 14i  24 j  6k

Sehingga bidang yang melalui titik
14i  24 j  6k mempunyai persamaan :
 Ax  x1   B y  y1   Cz  z1   0
 14x  4  24 y  1  6z  2  0
 14 x  56  24 y  24  6 z  12  0
 14 x  24 y  6 z  56  24  12  0
 14 x  24 y  6 z  44
Geometri dalam Ruang, Vektor
P2 4,1,2 dengan normal
165
P1 1,2,3 karena
juga terletak pada bidang dengan normal 14i  24 j  6k
Atau dapat juga ditentukan dengan mengambil titik
titik P1
mempunyai persamaan :
 Ax  x1   B y  y1   Cz  z1   0
 14x  1  24 y  2  6z  3  0
 14 x  14  24 y  48  6 z  18  0
 14 x  24 y  6 z  14  48  18  0
 14 x  24 y  6 z  44
Contoh 4.23 :

Perlihatkan bahwa luas jajaran genjang yang dibentuk oleh vector u

dan v sebagai sisi berdampingan adalah
u.x.v
Penyelesaian 4.23 :
Jika kita gambarkan secara geometri, maka sebagai berikut :
u
u Sin
v
Karena luas jajaran genjang itu adalah Luas  alas.x.tinggi dimana
alas.  v dan tinggi .  u Sin sehingga Luas jajaran genjang itu
adalah :
L  v u Sin dan karena u.x.v  u v Sin , maka terbukti bahwa
luas jajaran genjang di atas adalah
Geometri dalam Ruang, Vektor
L  u.x.v
166
Contoh 4.24 :
Sebuah jajaran genjang yang dibentuk dari dua buah vektor
u  3i  2 j  k dan vektor v  4i  2 j  3k adalah
Penyelesaian 4.24 :
Diketahui vektor u  3i  2 j  k dan v  4i  2 j  3k , maka
uv 
i
j
k
1
 uv  3  2
4 2 3
2 1
3 1
3 2
i
j
k
2 3 4 3
4 2
 u  v  6  2i   9  4 j  6  8k
 u  v  4i  13 j  14k

uv 
Luas jajaran genjang adalah

L  uv

L  4 2   13  14 2

L  16  169  196

L  381
L  uv
2
Geometri dalam Ruang, Vektor
167
4.3.2. Soal-Soal Latihan
A.
Dikebrikan u  3i  2 j  2k , v  i  4 j  3k dan
w  2i  j  4k tentukan :
1. uxv
2. ux(v  w)
3. u  (vxw)
4. ux(vxw)
B.
Tentukan vector satuan yang tegak lurus terhadap bidang
yang dibentuk oleh tiga titik yaitu :
1. A  1,2,0 , B 5,1,3 dan C 4,0,2
2.
C.


 


A0,1,5 , B2,2,2 dan C  3,4,1
Tentukan Luas Jajaran Genjang yang dibentuk dari vector A
dan B sebagai dua sisi yang berdampingan
1. A  2i  j  4k dan B  4i  2 j  5k
2. A  2i  5 j  2k dan B  3i  3 j  6k
D.
Tentukan Luas segitiga yang dibentuk dari tiga titik A, B dan
C yaitu :
1. A 3,2,1 , B 2,4,6 dan C  1,2,7
2.
E.



  
A 1,2,1 , B0,3,0 dan C 4,5,6
Tentukan persamaan bidang yang melalui tiga titik A, B dan
C yaitu
1. A 2,5,6 , B 1,1,2 dan C 4,0,6
2.
  
 

A 1,2,3 , B4,2,1 dan C 5,1,6
Geometri dalam Ruang, Vektor
168