Document

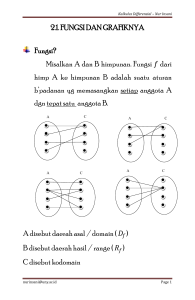
PRE UTS
Matematika dan Statistik
Purcell E.J., Varberg D., 2003, KALKULUS, edisi V, Erlangga, Jakarta.
Stewart, J., 1998, KALKULUS, edisi IV, Erlangga, Jakarta.
Vandermeer, J., 1981, Elementary Mathematical Ecology, Willey,
New York.
Walpole, R.E., 1995, Pengantar Statistika, edisi III, Gramedia,
Jakarta.
Fungsi
Sebuah Fungsi
f
adalah suatu aturan atau padanan yang
menghubungkan tiap objek x dalam satu himpunan, yang disebut daerah
asal, dengan sebuah nilai unik f(x) dari himpunan kedua. Himpunan nilai
yang diperoleh secara demikian disebut daerah hasil fungsi tersebut.
Notasi Fungsi memakai sebuah huruf tunggal seperti f (atau g atau F)
1
2
3
4
5
Pertemuan II
Daerah Asal dan Daerah Hasil Suatu Fungsi
Daerah asal adalah himpunan elemen-elemen pada mana fungsi itu
mempunyai nilai.
Daerah hasil adalah himpunan nilai-nilai yang diperoleh berdasarkan
aturan fungsi
1
2
3
4
5
Pertemuan II
Grafik Fungsi. Bilamana daerah asal dan daerah hasil sebuah fungsi
merupakan bilangan riil, kita dapat membayangkan fungsi itu dengan
menggambarkan grafiknya pada suatu bidang koordinat. Dan grafik
fungsi f adalah grafik dari persamaan y=f(x)
1
2
3
4
5
Pertemuan II
Kesimetrian Grafik
Jika f(-x)=f(x), maka grafik simetri terhadap sumbu y. Fungsi yang
demikian disebut fungsi genap.
Jika f(-x)=-f(x), maka grafik simetri terhadap titik asal. Fungsi yang
demikian disebut fungsi ganjil.
1
2
3
4
5
Pertemuan II
Fungsi Khusus
Fungsi Nilai Mutlak
 x
x 
 x
jika x  o
jika x  0
Fungsi Bilangan Bulat Terbesar
lebih kecil atau sama dengan x



= bilangan bulat terbesar yang
Gambarlah grafik dari kedua fungsi tersebut…
Apakah kedua fungsi tersebut merupakan fungsi genap ? atau fungsi
ganjil ?
1
2
3
4
5
Pertemuan II
Operasi pada dua buah fungsi
( f  g )( x)  f ( x)  g ( x)
( f  g )( x)  f ( x)  g ( x)
( f .g )( x)  f ( x). g ( x)
f 
f ( x)
 ( x) 
g ( x)
g
1
2
Pertemuan II
Operasi pada dua buah fungsi
Daerah asal fungsi hasil operasi dua fungsi adalah irisan dari
daerah asal masing-masing fungsi
1
2
Pertemuan II
( g  f )( x)  g ( f ( x))
Apakah sifat komutatif berlaku pada komposisi fungsi ?
Daerah asal dari fungsi komposit g ° f adalah bagian dari
daerah asal f untuk mana g dapat menerina f(x) sebagai
masukan.
1
Pertemuan II
LIMIT
Berapakah
lim
x 1
x 2 1
x 1
?
2
1
x
f(x)
0,9
1,9
0,99
1,99
0,999
1,999
0,9999
1,9999
1,1
2,1
1,01
2,01
1,001
2,001
Jawab : 2
1
2
3
Pertemuan II
Limit Kiri dan Limit Kanan
Ketika x dekat tetapi pada sebelah kanan c
lim f ( x)  L
Ketika x dekat tetapi pada sebelah kiri c
lim f ( x)  L
x c 
x c 
lim f ( x)  L
x c
1
2
3
jika dan hanya jika
lim f ( x)  L dan lim f ( x)  L
x c 
x c 
Pertemuan II
Teorema Limit Utama
1. lim k  k
x c
2. lim x  c
x c
3. lim kf ( x)  k lim
f ( x)
x c
x c
4. lim [ f ( x)  g ( x)]  lim
f ( x )  lim g ( x)
5. lim [ f ( x)  g ( x)]  lim
f ( x)  lim g ( x )
x c
x c
x c
x c
6. lim [ f ( x).g ( x)]  lim
x c
x c
7. lim
x c
f ( x)

g ( x)
x c
x c
f ( x ). lim g ( x )
x c
lim f ( x)
lim g ( x)
x c
x c
8. lim [ f ( x)]
x c
9. lim
x c
1
2
3
n
n


 lim f ( x ) 
 x c

f ( x) 
n
lim
x c
n
f ( x)
Pertemuan II
Jika f fungsi polinomial atau fungsi rasional, maka
lim f ( x)  f (c)
x c
asalkan pada kasus fungsi rasional nilai penyebut di c
tidak sama dengan nol
1
2
3
Pertemuan II
1
2
3
Pertemuan II