logika matematika

LA - WB
(Lembar Aktivitas Warga Belajar)
LOGIKA MATEMATIKA
Oleh:
Hj. ITA YULIANA, S.Pd, M.Pd
MATEMATIKA PAKET C
TINGKAT V DERAJAT MAHIR 1
SETARA KELAS X
Created By Ita Yuliana
37
Logika Matematika
Kompetensi Dasar
1.
2.
3.
4.
Memahami pernyataan dalam matematika dan ingkaran atau negasinya
Menentukan nilai kebenaran dari suatu pernyataan majemuk dan pernyataan berkuantor
Merumuskan pernyataan yang setara dengan pernyataan majemuk atau pernyataan
berkuantor yang diberikan
Menggunakan prinsip logika matematika yang berkaitan dengan pernyataan majemuk
dan pernyataan berkuantor dalam penarikan kesimpulan dan pemecahan masalah
Indikator
1. Warga belajar dapat menentukan pernyataan dan ingkaran dari suatu pernyataan
2. Warga belajar dapat menentukan nilai kebenaran dari disjungsi, konjungsi, dan
ingkarannya
3. Warga belajar dapat menentukan nilai kebenaran dari implikasi, konvers, invers, dan
kontraposisi beserta ingkarannya
4. Warga belajar dapat menjelaskan arti kuantor universal dan eksistensial beserta
ingkarannya
5. Warga belajar dapat merumuskan pernyataan majemuk yang ekuivalen beserta
ingkarannya
6. Warga belajar dapat menarik kesimpulan dari modus ponens, modus tolens, dan
silogisme
7. Warga belajar dapat membuktikan sifat matematika dengan bukti tak langsung
(kontraposisi dan kontradiksi)
8. Warga belajar dapat membuktikan sifat dengan induksi matematika
Kasus
Para eksekutif, guru, tutor, pelajar, dan pengusaha biasanya tidak mau ketinggalan berita di
koran. Mereka selalu menyempatkan diri untuk membaca berita di berbagai koran, dari berita
olahraga, ekonomi, pendidikan, hingga iklan.
Coba kamu perhatikan kalimat-kalimat pada potongan koran tersebut, adakah yang aneh?
Dalam matematika kita juga akan mempelajari tentang kalimat, salah satunya dalam bab
Logika Matematika. Di mana hubungan antara kalimat-kalimat itu dengan materi Logika
Matematika ? Kamu akan mendapatkan jawabannya.
Ringkasan Materi
A. Kalimat Terbuka, Pernyataan, dan Ingkaran
1. Kalimat Terbuka
Kalimat terbuka adalah suatu kalimat yang masih mengandung variabel. Suatu
kalimat terbuka akan menjadi sebuah pernyataan jika variabelnya diganti dengan
konstanta tertentu
Created By Ita Yuliana
38
Contoh :
a. 3x – 1 = 5
b. Benda dalam kotak itu sangat mahal
c. Hari ini akan terjadi angin puting beliung
Ketiga contoh di atas belum dapat ditentukan kebenarannya. Kebenarannya baru
dapat ditentukan jika variabel “x” dan kata “benda” itu diganti. Untuk 3x – 1 = 5,
jika x diganti dengan 2 maka menghasilkan kalimat yang tidak benar, sedangkan
jika x diganti dengan 2 maka akan mengahsilkan kalimat yang benar.
Kalimat matematika seperti itu disebut kalimat terbuka.
2. Pernyataan
Pernyataan adalah suatu kalimat yang telah mempunyai nilai. Nilai tersebut
mungkin bernilai benar saja atau salah saja, tetapi bukan keduanya.
Contoh:
a. Matahari terbit dari ufuk barat (pernyataan salah)
b. 3 – 1 = 2 (pernyataan benar)
c. Semarang adalah ibu kota provinsi Jawa Tengah (pernyataan benar)
3. Ingkaran (Negasi)
Ingkaran suatu pernyataan adalah pernyataan baru yang bernilai salah jika
pernyataan semula benar atau bernilai benar jika pernyataan semula salah.
Pernyataan “p” ingkarannya “tidak p” yang dilambangkan dengan atau
.
Tabel kebenaran:
p
Keterangan
B
S
B = Benar
S
B
S = Salah
Contoh:
a. Pernyataan p
maka
b. Pernyataan p
maka
c. Pernyataan p
maka
: 3 adalah merupakan bilangan ganjil
: Tidak benar 3 adalah bilangan ganjil atau 3 bukan bilangan ganjil
:7–3=5
: Tidak benar 7 – 3 = 5 atau 7 – 3  5
: Hari ini hari sabtu
: Tidak benar hari ini hari sabtu atau hari ini bukan hari sabtu
Aktivitas 1
1. Tuliskan
a. 3 pernyataan yang bernilai benar
b. 3 pernyataan yang bernilai salah
Created By Ita Yuliana
39
2.
Tentukan nilai kebenaran
a. Kuda adalah hewan berkaki empat
b. HP dari x2 – 6x + 9 = 0 adalah {3}
c. Semua bilangan genap habis dibagi 2
d. 2 bukan termasuk bilangan prima
e. 3 + (-5) – 7 + 8 = 3
B. Konjungsi dan Disjungsi
1. Konjungsi
Konjungsi adalah pernyataan majemuk dengan menggunakan kata hubung “dan”
dilambangkan “ ”
Tabel kebenaran
p
q
Keterangan
p q
B
B
B
B = Benar
B
S
S
S = Salah
S
B
S
S
S
S
Contoh:
Tentukan nilai kebenaran konjungsi berikut.
Pernyataan p : Bilangan 9 habis dibagi 3 (Benar)
Pernyataan q : Bilangan 9 merupakan bilangan genap (Salah)
p q
: Bilangan 9 habis dibagi 3 dan 9 merupakan bilangan genap (Salah)
B
S
=S
2. Disjungsi
Disjungsi adalah pernyataan majemuk dengan menggunakan kata hubung “atau”
dilambangkan “ ”
Tabel kebenaran
p
q
Keterangan
p q
B
B
B
B = Benar
B
S
B
S = Salah
S
B
B
S
S
S
Contoh:
Tentukan nilai kebenaran disjungsi berikut.
Pernyataan p : 4 adalah bilangan genap (Benar)
Pernyataan q : 4 adalah bilangan prima (Salah)
p q
: 4 adalah bilangan genap atau 4 adalah bilangan prima (Benar)
B
S
=B
Created By Ita Yuliana
40
Aktivitas 2
1. Tentukan nilai kebenaran dari konjungsi berikut ini
a. 4 + 3 = 7 dan kaki kuda berjumlah 4
b. -3 adalah bilangan bulat dan 3 adalah bilangan genap
c. 4 dan 5 adalah faktor dari 30
2. Tentukan nilai kebenaran dari disjungsi berikut ini
a. √ =  4 atau
=3
b.
– 4 = 0 atau 3 + 4 = 12
c. 8 faktor dari 32 atau 6 faktor dari 46
3. Diketahui :
p : Bangunan sekolah rusak
q : Sekolah libur
Nyatakan dengan kalimat pernyataan berikut ini.
a. p q
b. p q
c.
p q
d.
p q
4. Salin dan lengkapi tabel berikut
p
q
p q
B
B
B
S
S
B
S
S
p q
(p q)
(p q)
C. Implikasi dan Biimplikasi
1. Implikasi
Implikasi adalah pernyataan majemuk dengan kata hubung “jika ... maka ...”
dilambangkan “” atau “”
Implikasi p  q dapat juga dibaca
 p hanya jika q
 q jika p
 p syarat cukup bagi q
 q syarat perlu bagi p
Pada p  q, p disebut antiseden atau hipotesis dan q disebut konklusi
Created By Ita Yuliana
41
Tabel kebenaran
p
q
pq
B
B
B
B
S
S
S
B
B
S
S
B
Keterangan
B = Benar
S = Salah
Contoh:
Tentukan nilai kebenaran implikasi berikut
Pernyataan p : Roni anak ramah (Benar)
Pernyataan q : Roni mempunyai banyak teman (Benar)
pq
: Jika Roni ramah maka Roni mempunyai banyak teman (Benar)
B

B
=B
2. Biimplikasi / Ekuivalen
Biimplikasi adalah pernyataan majemuk dengan kata hubung “...jika dan hanya
jika ...” dilambangkan “” atau “”
Biimplikasi dapat juga dibaca
 Jika p maka q dan jika q maka p
 p syarat perlu dan cukup bagi q
 q syarat perlu dan cukup bagi p
Tabel kebenaran
p
q
pq
B
B
B
B
S
S
S
B
S
S
S
B
Keterangan
B = Benar
S = Salah
Contoh:
Tentukan nilai kebenaran biimplikasi berikut
Pernyataan p : 5 + 3 = 8 (Benar)
Pernyataan q : 4 x 2  8 (Salah)
pq
: 5 + 3 =8 jika hanya jika 4 x 2  8
B

S
(Salah)
=S
Aktivitas 3
1. Tentukan nilai kebenaran dari implikasi berikut
a. Jika 2 bilangan genap maka 7 bilangan ganjil
b. Jika 3 x 4 = 16 maka 16 bilangan prima
c. Jika 5 faktor dari 30 maka 5 faktor dari 16
Created By Ita Yuliana
42
2. Tentukan nilai x agar implikasi bernilai benar
a. x + 3 = 8  6 > 3
b. 3x – 6 = 3  2 > 7
c. 4 > 2  4x = 8
d. 3 bilangan ganjil  4x – 7 = 9
3. Diantara biimplikasi berikut, mana yang bernilai benar ?
a. 3 adalah bilangan prima jika dan hanya jika 3 faktor dari 10
b. 2 x 10 = 12 jika dan hanya jika 12 habis dibagi 2
c. 3 x 4 = 7 jika dan hanya jika 7 bukan bilangan prima
d. Manado ada di pulau Jawa jika dan hanya jika 2 bilangan genap
4. Tentukan x agar pernyataan berikut benar
a. 2 < 3  3x = 12
b. 4x – 5 = 2  3 > 6
c. 2x + 4 = 8  4 bilangan genap
D. Hubungan Konvers, Invers, dan Kontraposisi suatu Implikasi
Dari sebuah implikasi dapat diturunkan pernyataan yang disebut konvers, invers, dan
kontraposisi. Jika diketahui implikasi p  q maka akan berlaku sbb.
1. Konvers dari implikasi p  q adalah q  p
2. Invers dari implikasi p  q adalah

3. Kontraposisi dari implikasi p  q adalah q  p
Tabel kebenaran sbb.
p
q
B
B
S
S
B
S
B
S
S
S
B
B
S
B
S
B
pq
(implikasi)
B
S
B
B
(1)
qp
(konvers)
B
B
S
B
(2)
p q
(invers)
B
B
S
B
(3)

(kontraposisi)
B
S
B
B
(4)
Dari tabel di atas dapat disimpulkan
1. Suatu implikasi tidak ekuivalen dengan konversnya (kolom 1 dan 2)
2. Suatu implikasi tidak ekuivalen dengan inversnya (kolom 1 dan 3)
3. Suatu implikasi ekuivalen dengan kontraposisinya (kolom 1 dan 4)
ditulis p  q 

4. Konvers dari suatu implikasi ekuivalen dengan inversnya (kolom 2 dan 3)
ditulis q  p 

Created By Ita Yuliana
43
contoh:
Tentukan konvers, invers, dan kontraposisi dari pernyataan implikasi berikut
“Jika x = 1 maka x2 – 6x + 5 = 0”
Jawab:
 Konvers
: “ Jika x2 – 6x + 5 = 0 maka x = 1”
 Invers
: “ Jika x  1 maka x2 – 6x + 5  0”
 Kontraposisi : “ Jika x2 – 6x + 5  0 maka x  1”
Aktivitas 4
Tentukan konvers, invers, dan kontraposisi dari pernyataan implikasi berikut
1. “Jika harga BBM naik maka harga kebutuhan sehari-hari naik”
 Konvers
:
 Invers
:
 Kontraposisi :
2. “Jika x > 2 maka x2 > 2”
 Konvers
:
 Invers
:
 Kontraposisi :
3.
“Jika x bilangan genap maka x2 habis dibagi 4”
 Konvers
:
 Invers
:
 Kontraposisi :
Created By Ita Yuliana
44
E. Pernyataan Berkuantor
Pernyataan berkuantor adalah pernyataan yang melibatkan beberapa atau semua
anggota semesta pembicaraan yang mengawali sistem atau keadaan.
Ada dua macam pernyataan berkuantor yaitu kuantor universal dan kuantor
eksistensial
1. Kuantor Universal
Pernyataan berkuantor universal dilambangkan dengan “ ” dibaca “semua” atau
“setiap”
Contoh:
a. Semua orang berkaca mata
b. Jika untuk setiap x A maka berlaku 2x bilangan genap
c.
x B, 3x + 5 > 0
2. Kuantor Eksistensial
Pernyataan berkuantor eksistensial dilambangkan “” dibaca “ada” atau
“beberapa” atau “sebagian” yang mempunyai arti sekurang-kurangnya ada satu
atau paling sedikit satu
Contoh:
a. Ada santri yang berkaca mata
b. Beberapa siswa SMA menggunakan internet
c.  x A, 4x – 3 < 0
Aktivitas 5
1. Ubahlah setiap pernyataan berkuantor berikut ini ke bentuk simbolik yang
melibatkan implikasi
Contoh:
Semua kucing berkaki 4  Jika x adalah kucing maka x berkaki 4
a. Ada bilangan prima yang genap
b. Setiap bilangan prima lebih dari 2 adalah ganjil
2. Diantara setiap pasang pernyataan berkuantor universal dan implikasi berikut,
mana yang ekuivalen?
a. “Semua burung berbulu hitam”
“Jika x adalah burung maka x berbulu hitam”
b. “Semua bilangan asli adalah bilangan cacah”
“Jika x adalah bilangan cacah maka x adalah bilangan asli”
Created By Ita Yuliana
45
F. Pernyataan Majemuk
1. Pernyataan majemuk yang ekuivalen
Pernyataan majemuk yang ekuivalen adalah dua pernyataan yang mempunyai
nilai yang sama. Ekuivalen dilambangkan dengan “”
Berikut ini merupakan pernyataan-pernyataan yang ekuivalen
 p qq p
 p qq p
 p (q p)  (p q) p
 p (q r)  (p q) ( p r)
 p (q r)  (p q) ( p r)
 p (q r)  (p q) ( p r)
 pqp q
 p  q  (q  p) (q  p)
 pq  q p
2. Negasi (ingkaran) dari pernyataan majemuk
Jika akan membuat negasi pernyataan berkuantor maka harus berhati-hati dengan
arti “beberapa” dan “semua”
Berdasarkan pengertian pernyataan-pernyataan yang ekuivalen maka akan didapat
rumus yang disebut dengan Hukum de Morgan sebagai berikut.

(p q)  p
q

(p q)  p
q

(p  q)  p
q

(p  q)  (p
q) ( p q)
Contoh:
Tentukan negasi dari pernyataan berikut ini
a. Saya malas dan bodoh
b. Dian sedang makan soto atau bakso
c. Jika Amir rajin belajar maka ia pasti naik kelas
d. Ulangan dibatalkan jika dan hanya jika ada kerja bakti
Jawab:
a. Saya tidak malas atau tidak bodoh
b. Dian tidak makan soto dan bakso
c. Amir rajin belajar dan ia naik kelas
d. Ulangan dibatalkan dan tidak diadakan kerja bakti atau diadakan kerja bakti
dan ulangan tidak dibatalkan
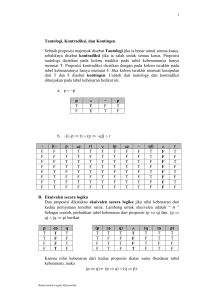
3. Tautologi
Tautologi adalah sebuah pernyataan majemuk yang selalu benar untuk semua
kemungkinan nilai kebenaran dari pernyataan-pernyataan komponennya.
Created By Ita Yuliana
46
Contoh:
p
B
B
S
S
q
B
S
B
S
p q
B
B
B
S
p(p q)
B
B
B
B
Semuanya bernilai benar
Jadi, p(p q) suatu tautologi
4. Kontradiksi
Kontradiksi adalah sebuah pernyataan majemuk yang selalu salah untuk semua
kemungkinan nilai kebenaran dari pernyataan komponennya.
Contoh:
p
q
B
B
B
S
S
B
S
S
p
S
S
B
B
q
S
B
S
B
p
S
S
S
B
q ( p
q)
S
S
S
S
p
Semuanya bernilai salah
Jadi, ( p q) p suatu
kontradiksi
Aktivitas 6
1. Tulislah pernyataan yang ekuivalen dengan pernyataan berikut
a. Saya pandai atau bodoh
b. Jika saya tidak merokok, maka saya sehat
c. Jika saya sakit maka saya tidak sekolah
d. Saya rajin atau malas bekerja
e. Jika saya malas maka saya tidak berhasil
2. Buatlah tabel kebenaran dari masing-masing pernyataan berikut, kemudian
tentukan apakah termasuk tautologi, kontradiksi atau kontingensi
a. (p q)  (q r)
c. (pq) ( q p)
b. (p q) r
d. [(pq) p]  p
Created By Ita Yuliana
47
G. Penarikan Kesimpulan
Pernyataan yang telah diketahui nilai kebenarannya disebut premis. Kumpulan semua
premis disebut argumen, dan pernyataan yang merupakan kesimpulan disebut konklusi
Penarikan kesimpulan di dalam logika matematika ada 3 cara yaitu:
1. Modus Ponens
Jika p benar dan p  q benar, dapat dinyatakan dengan:
pq
(benar)
premis 1
p
(benar)
premis 2
Jadi,
q
(benar)
kesimpulan
Contoh:
Jika Semarang kota di Pulau Jawa maka Makasar kota di Pulau Sulawesi
Semarang kota di Pulau Jawa
Jadi, Makasar kota di Pulau Sulawesi
2. Modus Tollens
Jika p  q benar dan
benar, maka
benar, dapat dinyatakan dengan:
pq
(benar)
premis 1
(benar)
premis 2
Jadi,
(benar)
kesimpulan
Contoh:
Jika suatu segitiga sama sisi maka semua panjang sisinya sama
Panjang semua sisinya tidak sama
Jadi, suatu segitiga itu bukan segitiga sama sisi
3. Prinsip Silogisme
Jika p  q benar dan q  r benar, maka p  r benar, dapat dinyatakan dengan:
pq
(benar)
premis 1
qr
(benar)
premis 2
Jadi, p  r
(benar)
kesimpulan
Contoh:
Jika hari hujan maka air sungai meluap
Hari ini hujan
Jadi, sungai meluap
Created By Ita Yuliana
48
Aktivitas 7
Buatlah kesimpulan dari pernyataan-pernyataan berikut ini
1. Semua warga belajar paket C berseragam putih abu-abu
Fendi warga belajar paket C
2. Jika layang-layang maka diagonalnya berpotongan tegak lurus
Diagonal AC dan BD tidak saling tegak lurus
3. Jika musim banjir maka harga beras mahal
Jika harga beras mahal maka Jefri akan sering berpuasa
4. Buktikan kebenaran dari pernyataan berikut
a. p  q
b. p  q
q
r q
Jadi, p
Jadi, q
H. Metode Pembuktian
1. Bukti Langsung
Bukti langsung yaitu membuktikan kebenaran suatu pernyataan secara langsung
dengan menggunakan fakta-fakta yang tersedia.
Modus ponens, modus tollens, dan silogisme termasuk pada cara pembuktian
sifat matematika secara langsung.
Contoh:
a.
b.
c.
d.
Jumlah sudut dalam segitiga adalah 1800 (B)
Dua garis yang saling sejajar memiliki gradien yang sama (B)
Hewan tidak pernah mati (S)
Satu bulan terdiri dari 3 minggu (S)
2. Bukti Tak Langsung
Bukti tak langsung adalah membuktikan kebenaran suatu pernyataan dengan
menunjukkan bahwa ingkarannya salah.
Contoh:
Buktikan bahwa “Jika n2 bilangan bulat ganjil maka n bilangan ganjil”
Jawab:
Created By Ita Yuliana
49
Misalkan,
pernyataan p
pernyataan q
pq
: Jika n2 bilangan bulat ganjil
: n bilangan ganjil
: Jika n2 bilangan bulat ganjil maka n bilangan ganjil
untuk membuktikan p  q benar, buktikan

2
pernyataan
: n bukan bilangan bulat ganjil
pernyataan
: n bukan bilangan bulat ganjil

: Jika n bukan bilangan bulat ganjil maka n2 bukan bilangan
bulat ganjil
Jelas bahwa

benar, sehingga p  q juga benar
Jadi, “jika n2 bilangan bulat ganjil maka n bilangan bulat ganjil” merupakan
pernyataan yang benar
3. Induksi Matematika
Untuk membuktikan kebenaran suatu rumus yang berhubungan dengan bilangan
asli n, digunakan induksi matematika.
Langkah-langkah induksi matematika, yaitu
a. tunjukkan bahwa rumus benar untuk n = 1
b. dianggap benar bahwa rumus berlaku untuk n = k
c. rumus dibuktikan kebenarannya untuk n = k + 1
contoh:
Dengan induksi matematika, buktikan bahwa
1 + 3 + 5 + 7 + . . . + (2n – 1) = n2
n suku
jawab:
a. Untuk n = 1 maka berlaku 1 = 12
b. Rumus dianggap benar untuk n = k
1 + 3 + 5 + 7 + . . . + (2k – 1) = k2
k suku
c. Untuk n = k + 1
Dibuktikan bahwa
1 + 3 + 5 + 7 + . . . + (2k – 1) + 2(k + 1) – 1 = (k + 1)2
k + 1 suku
Created By Ita Yuliana
50
ruas kiri
1 + 3 + 5 + 7 + . . . + (2k – 1) + 2(k + 1) – 1 = k2 + 2k + 2 – 1
= k2 + 2k + 1
= (k + 1)2 (ruas kanan)
Ini berarti rumus berlaku untuk n = k + 1
Karena rumus berlaku untuk n = 1, n = k, dan n = k + 1 maka rumus berlaku
untuk setiap bilangan asli n.
Aktivitas 8
Dengan induksi matematika buktikan bahwa pernyataan berikut benar
1. 1 + 2 + 22 + . . . + 2n-1 = 2n – 1
2. 1 + 4 + 7 + . . . + (3n – 2) = n (3n – 1)
Created By Ita Yuliana
51