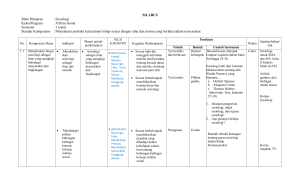
himpunan - Asep Irama

HIMPUNAN
By:
Meilani Safitri, M.Pd.
DEFINISI
• Kumpulan objek-objek yag terdefinisi
dengan jelas
PENYAJIAN HIMPUNAN
•
•
•
•
Enumerasi
Simbol Baku
Notasi Pembentuk Himpunan
Diagram Venn
ENUMERASI
Menuliskan semua elemen himpunan dalam
kurung kurawal
Contoh :
A adalah himpunan lima bilangan ganjil
positif pertama
A = {1,3,5,7,9}
SIMBOL BAKU
P = himpunan bilangan bulat positif
N = himpunan bilangan asli
Z = himpunan bilangan bulat
Q = himpunan bilangan rasional
R = himpunan bilangan riil
C = himpunan bilangan kompleks
NOTASI PEMBENTUK
HIMPUNAN
Contoh :
A adalah himpunan bilagan bulat lebih dari 3 kurang dari 5
A = {x I -3<x<5 , xEZ}
DIAGRAM VENN
S
A
KARDINALITAS
Jumlah elemen berbeda dalam sebuah
himpunan
Contoh :
A adalah himpunan huruf penbentuk kata
MATEMATIKA
maka : A = {m,a,t,e,i,k}
sehingga n(A) = 6
MACAM-MACAM HIMPUNAN
•
•
•
•
•
Himpunan Kosong
Himpunan Bagian/ Subset
Himpunan yang Sama
Himpunan yang Ekuivalen
Himpunan Saling Lepas
• Himpunan Kuasa
HIMPUNAN KOSONG
Himpunan dengan kardinal = 0
Contoh:
A adalah himpunan bilangan positif kurang
dari 1
A={ }
n(A) = 0
SUBSET
Jika dan hanya jika setiap anggota
himpunan A juga menjadi anggota
himpunan B dilambangkan dengan A  B
CONTOH :
•
A = { 0, 1, 2, 3, 4, 5, 6, 7 }
B = { 1, 2,3, 4 }
C = { 6, 7, 8, 9 }
HIMPUNAN YANG SAMA
A = B, jika setiap anggota himpunan A sama
dengan angota himpunan B atau sebaliknya
• Contoh :
• A = { m, u, r, a, h }
• B = { h, a, r, u, m }
HIMPUNAN EKUIVALEN
Jika n( A ) = n ( B ), ditulis A ~ B.
• Contoh :
• A = { m, e, r, a, h }  n ( A ) = 5
• B = { p, u, t, i, h }  n ( B ) = 5
HIMPUNAN SALING LEPAS
Jika tidak ada anggota A yang menjadi
anggota B , atau sebaliknya, ditulis A  B.
• Contoh :
• A = { 1, 3, 5, 7, 9, 11 }
• B = { 2, 4, 6, 8, 10, 12 }
HIMPUNAN KUASA
Contoh :
A = {1,2} maka P(A) = { {}, {1}, {2}, {1,2} }
INTERSECTION
Irisan himpunan A dan B ditulis A  B
adalah himpunan semua objek yang
menjadi anggota himpunan A sekaligus
menjadi anggota himpunan B
Contoh:
P = {a, b, c, d, e } dan Q = {d, e, f, g, h }.
Tentukan P  Q
Jawab : P  Q = { d, e }
UNION
• A  B = { x | x  A dan x  B }.
Contoh:
Bila P = {a, b, c, d, e } dan Q = {d, e, f, g, h }.
Tentukan P  Q
Jawab :
P  Q = { a, b, c, d, e, f, g, h }
Soal : Nyatakan himpunan berikut dalam bentuk notasi
pembentuk himpunan
1. B adalah bilangan Asli yang lebih dari 3 dan kurang
atau sama dengan 15
2. C adalah bilangan bulat lebih dari atau sama dengan
-5 tetapi kurang dari 10
3. D adalah bilangan ganjil kurang dari 20
Jawaban :
1. B = { x | 3 < x ≤ 15 , x  A}
2. C = { x | -5 ≤ x < 10 , x  B }
3. D = { x | x < 20 , x  L }
Diketahui: S = { 0,1,2,3,4,5,6,7,8,9,10,11,12,13,14 }
A = { 1,2,3,4,5,6 } B = { 2,4,6,8,10 } C = { 3,6,9,12 }
Gambarlah diagram Venn untuk menyatakan himpunan di atas
Jawab:
S
0
6 adalah anggota yg dimiliki
oleh himpunan A,B,C
A
7
9
3
12
6
C
13 11
1
3 dan 6 adalah anggota yg
dimiliki oleh himpunan A
dan C
5
2 4
14
8
10
B
2,4, 6 adalah anggota yg
dimiliki oleh himpunan A
dan B
Dari 32 siswa terdapat 21 orang gemar melukis, 16 orang gemar menari
dan 10 orang gemar keduanya.
a. Ada berapa orang siswa yang hanya gemar melukis?
b. Ada berapa orang siswa yang hanya gemar menari?
c. Ada berapa orang siswa yang tidak gemar keduanya?
Jawab:
N(S) = 32
Misalnya : A = {siswa gemar melukis}
B = {siswa gemar menari}
A  B = {siswa gemar keduanya}
n(A) = 21
n(B) = 16
n(A  B) = 10
Perhatikan Diagram Venn berikut
S
A
a. Ada 11 siswa yang hanya gemar melukis
B
b. Ada 6 siswa yang hanya gemar menari
11
10
6
c. Ada 5 siswa yang tidak gemar keduanya
5
Diketahui : S = { x | 10 < x ≤ 20, x  P }
M = { x | x > 15, x  S }
N = { x | x > 12, x  S }
Gambarlah diagram vennya
Jawab : S = { x | 10 < x ≤ 20, x  P } = { 11,12,13,14,15,16,17,18,19,20 }
M = { x | x > 15, x  S } = { 16,17,18,19,20}
N = { x | x > 12, x  S } = { 13,14,15,16,17,18,19,20}
M  N = { 16,17,18,19,20 }
Diagram Vennya adalah sbb:
S
N
11
12
16 18
13
17 19
14 15
20
M
Contoh 4:
Dari 60 siswa terdapat 20 orang suka bakso, 46 orang suka siomay dan 5
orang tidak suka keduanya.
a. Ada berapa orang siswa yang suka bakso dan siomay?
b. Ada berapa orang siswa yang hanya suka bakso?
c. Ada berapa orang siswa yang hanya suka siomay?
Jawab:
N(S) = 60
Misalnya : A = {siswa suka bakso}
B = {siswa suka siomay}
n(A) = 20
n(B) = 46
(A B)c = {tidak suka keduanya}
n((A B)c) = 5
Maka A B = {suka keduanya}
n(A B) = x
n(S) = (20 – x)+x+(46-x)+5
{siswa suka bakso saja} = 20 - x
{siswa suka siomay saja} = 46 - x
Perhatikan Diagram Venn berikut
S
A
20 - x
x
46 - x
B
5
60 = 71 - x
X = 71 – 60 = 11
a. Yang suka keduanya adalah x
= 11 orang
b. Yang suka bakso saja adalah
20-x = 20-11= 9 orang
c. Yang suka siomay saja adalah
46-x = 46-11= 35 orang
LATIHAN - 1
Diketahui ;
A = { bilangan asli kurang dari 5 }
B = { bilangan ganjil kurang dari 9 }
C = { bilangan prima kurang dari 13 }
D = { warna lampu lalu lintas }
Pembahasan
A = { 1, 2, 3, 4 }
 n(A) =
B = { 1, 3, 5, 7 }
 n(B) =
C = { 2, 3, 5, 7, 11 }
 n(C) =
D = { merah, kuning, hijau } n(D) =
4
4
5
3
A ~ B jika banyak anggota A dan B sama.
Jadi Himpunan yang ekuivalen adalah A dengan B,
Ditulis A ~ B.
LATIHAN - 2
Diketahui ;
A = { m, e, r, a, h }
B = { 1, 2, 3, 4, 5, 6, 7 }
C = { a, e, i, o, u }
D = { 2, 3, 5, 7, 11, 13}
Himpunan yang ekuivalen adalah . . .
Pembahasan
n (A) = 5
n (C) = 5
n (B) = 7
n (D) = 6
Himpunan yang ekuivalen adalah :
A dengan C
LATIHAN - 3
A = { faktor dari 12 }
B = { bilangan prima kurang dari 15 }
AB=....
Pembahasan
A = { 1, 2, 3, 4, 6, 12 }
B = { 2, 3, 5, 7, 11, 13 }
A  B adalah anggota yang sama
A  B = { 2, 3 }
LATIHAN - 4
K = { k, o, m, p, a, s }
L = { m, a, s, u, k }
K  L =....
Pembahasan
K = { k, o, m, p, a, s }
L = { m, a, s, u, k }
K  L = anggota yang sama.
K  L = { k, m, a, s }
LATIHAN-5
Dalam satu kelas, 25 orang di
antaranya senang basket, 35 orang
senang voli, dan 15 orang senang
keduanya. Banyak siswa dalam
kelas itu adalah …
Pembahasan
Basket
= 25 orang
Volli
= 35 orang
Basket dan Volli = 15 orang
Jumlah siswa dalam kelas =
( 25 org + 35 orang ) – ( 15 orang ) =
45 orang.
LATIHAN - 6
Penderita demam berdarah maupun
muntaber yang dirawat di rumah sakit
sebanyak 86 orang, 35 orang menderita
demam berdarah, dan 15 orang menderita
demam berdarah juga muntaber. Banyak
penderita yang hanya menderita muntaber
adalah . . .
Pembahasan
Jumlah pasien
= 86 orang.
Demam berdarah
= 35 orang.
DBD dan muntaber = 15 orang.
Muntaber
= X orang.
X = ( 86 org ) - ( 35 org + 15 org ) =
X = 86 org – 50 org
X = 36 orang
LATIHAN - 7
Dari 25 orang anak, ternyata 17 anak
gemar minum kopi, 8 anak gemar
minum teh, 3 anak tidak gemar
minum keduanya. Banyaknya anak
yang gemar keduanya adalah . . .
Pembahasan
Kopi
= 17 anak
Teh
= 8 anak
Kopi dan Teh = x anak
Tidak keduanya = 3 anak
(17 + 8 ) - x = 25 - 3  25 - x = 22
X = 25 – 22 = 3
Yang gemar keduanya adalah 3
anak.