Persamaan dan Tempat Kedudukan

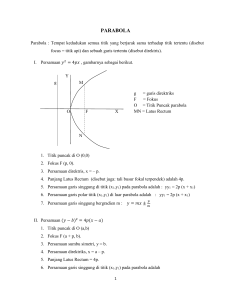
BAB 6 Parabola
6
Parabola
6.1. Persamaan Parabola Bentuk Baku
Parabola didefinisikan sebagai tempat kedudukan titik-titik P(x, y) pada
bidang sedemikian hingga titik itu berjarak sama dari suatu titik tertentu yang disebut
fokus dan garis tertentu yang tidak memuat fokus dan disebut direktrik.
Untuk menentukan persamaan parabola, pertama ditinjau parabola dengan
fokus berada pada sumbu-x dan dengan direktrik tegak lurus sumbu-x. Sedangkan
sumbu-y diletakkan di tengah-tengah segmen garis hubung dari titik fokus F ke
garis direktrik d.
Y
D
P(x, y)
F(c, 0)
X
x = –c
O
Gambar 6.1
6.1. Bentuk Baku Parabola  195
BAB 6 Parabola
Misalkan jarak antara garis direktrik dengan fokus adalah 2c, maka koordinat
titik fokusnya adalah F(c, 0) dan persamaan garis direktrik d adalah x = –c, c  0.
(lihat gambar 6.1).
Jika P(x, y) adalah sembarang titik pada parabola, maka dari definisi kurva
parabola diperoleh hubungan
PF = PD
( x  c) 2  y 2 = |x + c|
yaitu

(x – c)2 + y2 = (x + c)2

x2 – 2cx + c2 + y2 = x2 + 2cx + c2

y2 = 4cx
(1)
Persamaan (1) di atas merupakan persamaan parabola yang dicari yaitu
parabola yang mempunyai fokus F dengan koordinat (c, 0) dan persamaan garis
direktrik d  x = –c, c  0.
Jika dilakukan pertukaran x dan y dalam (1) maka diperoleh
x2 = 4cy,
(2)
yang mana (2) merupakan persamaan parabola dengan fokus di titik (0, c) pada
sumbu-y dan garis direktrik dengan persamaan d  y = –c.
6.1. Bentuk Baku Parabola  196
BAB 6 Parabola
Persamaan (1) dan (2) dikenal sebagai persamaan parabola bentuk baku.
Jika c adalah positif, maka parabola adalah terbuka ke arah sumbu-x atau
sumbu-y positif; sebaliknya jika c adalah negatif, maka parabola adalah terbuka ke
arah sumbu-x atau sumbu-y negatif, bergantung parabola bentuk baku (1) atau (2).
Sekarang kita perhatikan beberapa sifat dari parabola sebelum melanjutkan ke
permasalahan yang lain. Pertama parabola adalah kurva yang simetrik. Garis simetri
dari parabola disebut sumbu parabola. Garis ini tegak lurus dengan direktrik dan
memuat titik fokus. Titik potong sumbu dengan parabola disebut puncak (vertex).
L
2c
D
2c
c
E V
D’
c
F
2c
2c R
Gambar 6.2.
Tali busur parabola yang melalui fokus dan tegak lurus sumbu parabola
disebut latus rectum parabola. Panjang latus rektum dapat dihitung secara langsung
dari gambar 6.2, yang mana latus rektum adalah segmen garis LR. Fokus dan puncak
parabola F dan V, sedangkan direktriknya d = DD ' . Sumbu parabola dan
garisdirektrik berpotongan di E. Berdasarkan definisi parabola, LF = LD = |2c|. Jadi
panjang laktus rektum adalah LR = |4c|.
6.1. Bentuk Baku Parabola  197
BAB 6 Parabola
6.2. Konstruksi Geometrik dari Parabola
Sebuah parabola yang diketahui fokus dan direktriknya dapat segera
dikonstruksi dengan penggaris dan jangka sebagai berikut:
Misalkan F adalah fokus dan d direktrik yang diberikan (lihat gambar 6.3).
Gambar sumbu parabola EF, yang tentu saja memuat titik fokus F dan tegak lurus
dengan garis d berpotongan di E. Puncak parabola V adalah titik tengah antara E dan F.
d
P
D
E
D’
V
B
F A
P’
Gambar 6.3.
Ambil sembarang titik A pada sumbu dan berada pada sisi yang sama dengan
F terhadap titik V. Melalui A lukis garis AB yang sejajar dengan direktrik (atau tegak
lurus dengan sumbu parabola).
Dengan F sebagai pusat dan jari-jari sama dengan panjang EA, lukis busur
yang memotong AB di P dan P’. Maka P dan P’ adalah titik-titik pada parabola yang
6.2. Konstruksi Geometrik Parabola  198
BAB 6 Parabola
dicari, karena PF = AE = PD, yaitu titik yang berjarak sama terhadap titik F dan garis
d. Secara sama dapat diujikan untuk titik P’.
Dengan mengubah posisi titik A dapat dikonstruksikan sebanyak titik yang
diinginkan pada parabola. Secara praktis, akan sangat memudahkan, apabila pada
langkah awal dilukis sejumlah garis sejajar dengan direktrik untuk memperoleh titik
anggota tempat kedudukan.
Suatu cara yang sangat mudah dilakukan dalam memvisualisasikan bentuk
parabola adalah dengan menggunakan sehelai benang. Jika sehelai benang yang
lentur ujung-ujungnya dikaitkan pada paku pada dinding yang rata, maka lengkungan
benang yang menggantung akan membentuk parabola.
Contoh 1:
Tentukan koordinat fokus dan persamaan direktrik parabola dengan persamaan
y2 = –8x. Lukis grafik parabola tersebut.
Jawab:
Dengan membandingkan persamaan parabola dalam bentuk baku (1) maka
diperoleh hubungan
4c = –8

c = –2
6.2. Konstruksi Geometrik Parabola  199
BAB 6 Parabola
Jadi parabola di atas mempunyai titik fokus di (–2, 0).
Persamaan garis direktriknya adalah x = 2.
Untuk melukis grafik parabola di atas, pertama dilukis garis direktrik dan
fokusnya. Kemudian buat sketsa grafik dengan menentukan beberapa titik yang
berjarak sama dari fokus dengan direktrik. Sketsa grafik dapat diperlihatkan
dalam gambar 6.4.
Y
x=2
F
(-2, 0)
O
X
Gambar 6.4.
Contoh 2:
Tentukan persamaan parabola dengan puncak di titik asal (0, 0)dan titik fokus
di (–4, 0).
Jawab:
Karena fokus dan puncak pada sumbu-x, maka sumbu-x adalah sumbu parabola.
6.2. Konstruksi Geometrik Parabola  200
BAB 6 Parabola
Jadi persamaan parabola dalam bentuk y2 = 4cx.
Karena fokusnya adalah (–4, 0), maka c = –4 dan persamaannya adalah
y2 = 4(–4)x
atau
y2 = –16x
Contoh 3:
Tentukan persamaan parabola yang mempunyai puncak titik asal dan melalui
titik (8, 10),
(a) jika sumbu parabola berimpit dengan sumbu-x,
(b) jika sumbu parabola berimpit dengan sumbu-y.
Jawab:
(a) Karena sumbu parabola berimpit dengan sumbu-x, maka persamaan
bakunya berbentuk (1) yaitu y2 = 4px. Dengan mensubstitusikan koordinat
(8, 10) ke persamaan diperoleh 100 = 32p, p =
yang dicari adalah y2 =
25
2
25
8
. Jadi persamaan parabola
x.
(b) Karena sumbu parabola berimpit dengan sumbu-y, maka persamaan
bakunya berbentuk (1) yaitu x2 = 4py. Dengan mensubstitusikan koordinat
(8, 10) ke persamaan diperoleh 64 = 40p, p =
yang dicari adalah x2 =
32
5
8
5
. Jadi persamaan parabola
y.
6.2. Konstruksi Geometrik Parabola  201
BAB 6 Parabola
6.3. Aplikasi Parabola
Lintasan peluru meriam yang ditembakkan dari suatu tempat dengan sudut
elevasi tertentu, dengan mengabaikan resistensi udara dan lainnya, adalah sebuah
parabola. Kabel pada jembatan gantung yang mempunyai distribusi beban seragam
akan menggantung dalam bentuk parabola. Arsitektur jembaran atau ornamen pada
sebuah gedung kadang-kadang dibuat dalam bentuk parabolik.
Ada dua sifat yang menarik dari parabola yang mempunyai terapan dalam
konstruksi lampu sorot, lampu mobil dan teleskop. Sebuah parabola yang diputar
terhadap sumbunya akan membentuk sebuah permukaan. Jika permukaan cekung
pada benda ini digunakan sebagai reflektor, sinar cahaya yang datang secara paralel
dengan sumbu akan diarahkan ke fokus. Sebaliknya, jika sebuah sumber cahaya
dipancarkan dari fokus, maka cahaya akan dipantulkan ke luar dalam bentuk cahaya
yang sejajar.

T
F

O
P
R
Gambar 6.5.
6.3. Aplikasi Parabola  202
BAB 6 Parabola
Dalam gambar 6.5. misalkan P adalah sembarang titik pada grafik suatu
parabola dan PT adalah garis singgung di titik P. F adalah fokus parabola, dan 
adalah sudut antara FP dan garis singgung PT. PR sejajar dengan sumbu parabola,
dan  sudut antara PR dan PT. Dapat dibuktikan (dalam latihan 6 C) bahwa  = .
Dengan penjelasan ini, kepala lampu senter, permukaan kepala lampu
kendaraan, dan sebagainya dibuat dalam bentuk parabolik. Tetapi reflektor pada
teleskop, detektor suara parabolik, antena radio atau televisi berbentuk parabolik
dibuat berdasar pada prinsip yang berkebalikan (gambar 6.6). Pada teleskop, sinar
cahaya dari suatu obyek di langit yang jatuh ke cermin dan sejajar dengan sumbu
parabola akan dipantulkan dan dikumpulkan pada fokusnya.
Gambar 6.6 :
6.3. Aplikasi Parabola  203
BAB 6 Parabola
Latihan 6 A.
Pada masing-masing parabola berikut, tentukan koordinat fokus, persamaan direktrik
dan panjang latus rektum.
1. y2 = 12x.
7. 5y2 = 2x.
2. x2 = 4y.
8. 10x = y2.
3. 2y2 = 5x.
9. y2 = 4x.
4. y2 = 2x.
10. x= y2.
5. y2 = –12x.
11. y2 + 8x = 0.
6. x2 = –6y.
12. y = ax2.
Tentukan persamaan parabola jika diberikan data-data berikut:
13. Fokus (6, 0), direktrik x = –6.
14. Fokus (–4, 0), puncak pada titik asal.
15. Puncak pada titik asal, sumbu berimpit dengan sumbu-x, melalui titik (3, 2).
Apakah koordinat fokus dari parabola ini.
16. Latus rektum sama dengan 8, puncak pada titik asal, sumbu berimpit dengan
sumbu-y.
Latihan 6 A  204
BAB 6 Parabola
17. Melalui titik-titik (5, 4), (5, –4), dan titik asal, sumbu berimpit dengan sumbu-x.
Tentukan pula koordinat fokusnya.
18. Direktrik x = 6, puncak pada titik asal.
19. Ujung latus rektum pada titik (2, 4) dan (2, –4), puncak pada titik asal.
20. Fokus pada (0, –4), direktrik sejajar dan di atas sumbu-x, panjang latus rektum
sama dengan 16.
21. Tentukan persamaan lingkaran yang melalui puncak dan titik-titik ujung latus
rektum parabola y2 = 4x.
22. Suatu kurva berbentuk parabola memotong alas sepanjang 20 inci, ujungnya
setinggi 8 inci dari alas. Tentukan panjang tali busur yang sejajar dengan alas
dan berada di atas alas setinggi 6 inci.
23. Kabel pada suatu jembatan gantung, menggantung membentuk parabola diantara
dua menara yang berjarak 600 kaki. Ujung kabel diikat pada menara setinggi 110
kaki dari jalan raya dan titik terendah kabel setinggi 10 kaki dari jalan raya.
Tentukan total panjang lengan pengangkat jika tiap 50 kaki diberi lengan
pengangkat.
Latihan 6 A  205
BAB 6 Parabola
Dengan menggunakan definisi parabola secara langsung, tentukan persamaan
parabola, jika diberikan fokus dan direktriknya sebagai berikut:
24. Fokus (6, 0), direktrik sumbu-y.
25. Fokus (5, –4), direktrik garis x – 3 = 0.
26. Fokus (0, 0), direktrik garis x + 4 = 0.
27. Fokus (8, –4), direktrik garis y – 2 = 0.
28. Fokus (–6, 2), direktrik sumbu-y.
29. Fokus (–2, 0), direktrik garis x – 4 = 0.
30. Fokus (2, 1), direktrik garis 3x + 4y = 0.
31. Fokus (0, 0), direktrik garis x + y – 6 = 0.
32. Fokus (4, –3), direktrik y = x.
33. Fokus (0, 1), direktrik garis 5x + 12y – 13 = 0.
34. Fokus (2, 4), direktrik garis 12x – 5y = 0.
35. Radius fokal sebuah titik pada parabola adalah garis yang menghubungkan fokus
dengan titik tersebut. Tunjukkan bahwa radius fokal titik (x, y) pada parabola
y2 = 4px mempunyai panjang |x + p|.
Latihan 6 A  206
BAB 6 Parabola
6.4. Persamaan Parabola Bentuk Umum
Dengan merujuk pada penjelasan tentang translasi sumbu, jika puncak
parabola di titik V dengan koordinat (h, k) maka akan diperoleh persamaan parabola
yang lebih umum, dan persamaan baku parabola (1) dan (2) dari seksi 6.1 akan
berubah menjadi berturut-turut
(y – k)2 = 4c(x – h)
(1)
(x – h)2 = 4c(y – k)
(2)
Persamaan (1) di atas adalah persamaan parabola yang berpuncak di (h, k),
dengan titik fokus (h + c, k) dan direktrik x = h – c. Sedangkan fokus parabola dengan
persamaan (2) adalah (h, c + k) dan direktrik y = k – c.
Penjabaran lebih lanjut dari persamaan parabola (1) menghasilkan
(y – k)2 = 4c(x – h)


y2 – 2ky + k2 = 4cx – 4ch
y2 – 4cx – 2ky + k2 + 4ch = 0
Secara umum persamaan (1) dapat direduksi dalam bentuk
Cy2 + Dx + Ey + F = 0
(3)
6.4. Bentuk Umum Parabola  207
BAB 6 Parabola
dengan C dan D tidak sama dengan nol yang menyatakan persamaan parabola dengan
sumbu simetrinya sejajar dengan sumbu-x.
Secara sama persamaan (2) dapat direduksi dalam bentuk
Ax2 + Dx + Ey + F = 0
(4)
dengan A dan E tidak sama dengan nol yang menyatakan persamaan parabola dengan
sumbu simetrinya sejajar dengan sumbu-y.
Persamaan (3) dan (4) di atas dikenal sebagai bentuk umum persamaan
parabola.
Contoh 1:
Tentukan persamaan parabola yang mempunyai fokus di titik (7, 2) dan dengan
direktrik garis x = 1. Buat sketsa grafiknya.
Jawab:
Puncak parabola berada di tengah antara fokus dan direktrik. Dengan mudah
dapat diperoleh bahwa titik puncak parabola berada pada titik (4, 2). Jadi h = 4
dan k = 2.
Karena direktrik parabola adalah garis x = 1, maka parabola yang dicari
bersesuaian dengan persamaan (1) dan berlaku
6.4. Bentuk Umum Parabola  208
BAB 6 Parabola
h–c=1
c = h – 1 = 4 – 1 = 3.
Jadi persamaan parabola bentuk baku yang dicari adalah
(y – 2)2 = 43 (x – 4)

(y – 2)2 = 12(x – 4)
Parabola diatas dapat direduksi menjadi dalam bentuk umum
y2 – 12x – 4y + 52 = 0.
Sketsa grafik dapat dilihat pada gambar 6.7 berikut.
x=1
Y
F(7, 2)
V(4, 2)
X
O
Gambar 6.7.
Contoh 2:
Sebuah parabola mempunyai persamaan
3x2 + 6x + 12y = 5
6.4. Bentuk Umum Parabola  209
BAB 6 Parabola
Nyatakan ke dalam bentuk baku, kemudian tentukan puncak, titik fokus dan
direktrik dari parabola tersebut.
Jawab:
Kita ubah bentuk persamaan di atas ke dalam bentuk baku seperti pada
persamaan (2)
3x2 + 6x + 8y = 5

3x2 + 6x = – 8y + 5

3(x2 + 2x) = – 8y + 5

3(x2 + 2x + 1 – 1) = – 8y + 5

3(x + 1)2 – 3 = – 8y + 5

3(x + 1)2 = – 8y + 8

3(x + 1)2 = – 8(y – 1)

(x + 1)2 = –
8
(y – 1)
3
Dengan membandingkan persamaan ini dengan persamaan (2) maka diperoleh
informasi
6.4. Bentuk Umum Parabola  210
BAB 6 Parabola
h = –1, k = 1
dan
4c = –
8
3

c=–
2
3
Jadi dapatlah disimpulkan bahwa parabola yang terjadi berpuncak di (–1, 1),
titik fokusnya adalah (–1, 1 + (–
1
2
)) = (–1, ); dan garis direktriknya
3
3
y = 1 – (–
2
)
3

y=
5
3
Sketsa grafik dapat dilihat di gambar 6.8.
V(-1, 1)
Y
y=
F(7, 2)
5
3
X
O
Gambar 6.8.
Contoh 3:
Tentukan persamaan parabola yang sumbu simetrinya sejajar dengan sumbu-y,
berpuncak di P(2, 3) dan melalui titik Q(4, 5)
6.4. Bentuk Umum Parabola  211
BAB 6 Parabola
Jawab:
Bentuk baku dari persamaan parabola yang mempunyai sumbu simetri sejajar
dengan sumbu-y dan berpuncak di (h, k) adalah
(x – h)2 = 4c(y – k)
Karena parabola yang diminta berpuncak di P(2, 3), maka persamaan parabola
dalam bentuk
(x – 2)2 = 4c(y – 3)
Titik Q(4, 5) terletak pada parabola, maka berlaku
(4 – 2)2 = 4c(5 – 3)

c=½
Jadi persamaan parabola yang diminta adalah
(x – 2)2 = 4½ (y – 3)

x2 – 4x – 2y + 10 = 0
6.4. Bentuk Umum Parabola  212
BAB 6 Parabola
Latihan 6 B.
Pada soal 1 – 6 tentukan persamaan parabola jika diberikan data-data sebagai
berikut: Buat sketsa grafiknya.
1. Puncak di titik (2, 3); fokus di titik (5, 3).
2. Puncak (2, 5); fokus (2, 1).
3. Fokus (6, 1); direktrik sumbu-y.
4. Puncak (3, 1); direktrik y = 3
5. Puncak (–4, –3); direktrik x = 6.
6. Puncak (4, –2); latus rektum sama dengan 8; sumbu parabola y + 2 = 0.
7. Ujung-ujung latus rektum (–2, –7) dan (6, –7), parabola menghadap ke atas.
8. Ujung-ujung latus rektum (3, 1) dan (3, 5), parabola menghadap ke kanan.
9. Absis salah satu ujung latus rektum adalah 5, puncak parabola di (1, –1), sumbu
parabola sejajar dengan sumbu-y.
10. Fokus (4, 5), garis x = 4 menjadi sumbu simetri, dan melalui titik (2, 3).
Latihan 6 B  213
BAB 6 Parabola
6.5. Persamaan Garis Singgung pada Parabola.
Seperti halnya pada lingkaran dan ellips, terdapat dua macam garis singgung
yang akan dibicarakan, yaitu garis singgung yang melalui salah satu titik pada
parabola dan garis singgung yang mempunyai kemiringan tertentu.
6.5.1. Persamaan Garis Singgung yang mempunyai kemiringan m.
6.5.1.1. Pada parabola yang membuka ke kiri/kanan
Sekarang dibahas garis singgung suatu parabola yang mempunyai kemiringan
tertentu.
Misalkan kita akan mencari persamaan garis singgung parabola y2 = 4cx
yang mempunyai kemiringan m (lihat gambar 6.9).
Y
l  y = mx + b
y2 = 4cx
X
O
Gambar 6.9:
6.5. Persamaan Garis Singgung Parabola  214
BAB 6 Parabola
Karena kemiringan garis singgung l sudah diketahui maka dimisalkan
mempunyai persamaan garis yaitu keluarga garis dengan kemiringan m;
l  y = mx + b,
dengan b konstanta yang belum diketahui.
Jika persamaan garis itu disubstitusikan ke persamaan parabola akan diperoleh
hubungan
(mx + b)2 = 4cx

m2x2 + (2mb – 4c)x + b2 = 0
(1)
Oleh karena garis menyinggung parabola maka haruslah memotong pada satu
titik saja, dengan kata lain persamaan kuadrat di atas haruslah mempunyai
penyelesaian yang kembar. Hal itu berarti nilai diskriminannya haruslah nol.
Kondisi ini diberikan oleh persamaan :
(2mb – 4c)2 – 4m2b2 = 0
Persamaan di atas akan memberikan selesaian untuk b
b =
c
,m0
m
Jadi persamaan garis singgung parabola y2 = 4cx yang mempunyai kemiringan
m adalah
6.5. Persamaan Garis Singgung Parabola  215
BAB 6 Parabola
l  y = mx +
c
m
(2)
Persamaan garis singgung parabola (y – k)2 = 4c(x – k) yang berpuncak di titik
(h, k) dan sumbu parabola sejajar dengan sumbu-x, jika garis mempunyai kemiringan
m, dapat diperoleh dengan mentranslasikan persamaan (2) sedemikian hingga titik
asal berpindah ke titik (h, k). Dengan translasi ini diperoleh persamaan garis:
y – k = m(x – h) +
c
m
(3)
Contoh 1:
Tentukan persamaan garis singgung parabola y2 + 6y – 8x + 25 = 0 yang tegak
lurus garis 2x + y – 3 = 0.
Jawab:
Kita tulis kembali persamaan parabola
y2 + 6y = – 8x + 25
Dengan melengkapkan kuadrat persamaan parabola pada suku yang memuat y
pada ruas kiri diperoleh bentuk :
(y + 3)2 = 8x – 16
6.5. Persamaan Garis Singgung Parabola  216
BAB 6 Parabola

(y + 3)2 = 42(x – 2)
Persamaan terakhir adalah bentuk baku dari persamaan parabola dengan puncak
(2, –3) dan c = 2, yaitu h = 2, dan k = –3.
Misalkan m adalah kemiringan garis singgung yang dicari. Garis 2x + y – 3 = 0
mempunyai kemiringan –2, sedangkan garis singgung yang diminta tegak lurus
dengan di atas, yang berarti perkalian antar kemiringan garis sama dengan –1.
Jadi
m.(–2) = –1

m = ½.
Dengan persamaan (3) di atas maka persamaan garis singgung yang dicari
adalah :
y + 3 = ½(x – 2) +

2
1
2
x – 2y = 0
Jadi persamaan garis singgung yang dicari adalah
x – 2y = 0
6.5.1.2. Pada parabola yang membuka ke atas/bawah
Perhatikan bahwa persamaan garis singgung seperti tertuang baik dalam
persamaan (2) maupun (3) di atas hanya berlaku pada parabola yang sumbu
6.5. Persamaan Garis Singgung Parabola  217
BAB 6 Parabola
simetrinya berimpit atau sejajar sumbu-x. Jika sumbu simetrinya sejajar dengan
sumbu-y, atau membuka ke atas/bawah maka rumus tersebut tidak berlaku.
Persamaan baku parabola yang berpuncak di titik asal dan sumbu simetrinya
berimpit dengan sumbu-y adalah x2 = 4cy. Misalkan persamaan garis singgung
parabola itu mempunyai kemiringan m, dan kita misalkan berbentuk
l  y = mx + b
dengan b konstanta yang belum diketahui.
Jika y disubstitusikan pada parabola diperoleh
x2 = 4c(mx + b)
x2 – 4cmx – 4cb = 0
(4)
Dengan penjelasan yang sama dalam menurunkan rumus (3) maka l
menyinggung parabola maka diskriminan persamaan kuadrat (4) haruslah nol. Hal itu
diberikan oleh persamaan
(4cm)2 – 4(–4cb) = 0
yang memberikan penyelesaian untuk b yaitu :
b = –cm2
Jadi persamaan garis singgung yang dicari adalah
6.5. Persamaan Garis Singgung Parabola  218
BAB 6 Parabola
y = mx – cm2
(5)
Demikian pula untuk memperoleh persamaan garis singgung parabola yang
lebih umum (x – h)2 = 4c(y – k) yang berpuncak di titik (h, k) dan sumbu parabola
sejajar dengan sumbu-y, jika garis mempunyai kemiringan m, dapat diperoleh dengan
mentranslasikan persamaan (5) sedemikian hingga titik asal berpindah ke titik (h, k).
Dengan translasi ini diperoleh persamaan garis:
y – k = m(x – h) – cm2
(6)
Contoh 2:
Tentukan titik potong garis singgung parabola x2 – 4x – 4y – 8 = 0 yang
mempunyai kemiringan 3 dengan sumbu-sumbu koordinat.
Jawab:
Pertama dicari persamaan garis singgungnya, kemudian ditentukan titik potong
garis tersebut dengan sumbu-sumbu koordinat.
Tulis kembali persamaan parabola dalam bentuk :
x2 – 4x = 4y + 8
6.5. Persamaan Garis Singgung Parabola  219
BAB 6 Parabola
Dengan melengkapkan kuadrat sempurna pada ruas kiri persamaan parabola
dapat ditulis ke dalam bentuk baku
(x – 2)2 = 4y + 12

(x – 2)2 = 4(y + 3)
Persamaan terakhir adalah bentuk baku dari persamaan parabola dengan puncak
(2, –3) dan diperoleh h = 2, k = –3. Dan juga 4c = 4 atau c = 1.
Garis singgung yang dicari mempunyai kemiringan m = 3.
Dengan menggunakan persamaan (6) maka persamaan garis singgung yang
dicari adalah :
y + 3 = 3(x – 2) – 132
y + 3 = 3x – 6 – 9
3x – y – 18 = 0
Jadi persamaan garis singgung yang dicari adalah
3x – y – 18 = 0
Dengan demikian titik potong dengan sumbu-x dapat ditentukan dengan
memberi nilai y = 0 pada garis singgung sehingga diperoleh x = 6. Jadi
memotong sumbu-x di titik (6, 0).
6.5. Persamaan Garis Singgung Parabola  220
BAB 6 Parabola
Hal yang sama dapat dilakukan untuk memperoleh titik potong dengan sumbu-y
dengan memberi nilai x = 0, sehingga diperoleh y = 18. Jadi memotong sumbuy di titik (0, 18).
6.5.2. Persamaan Garis Singgung yang melalui titik di Parabola.
6.5.2.1. Pada parabola yang membuka ke kiri/kanan
Untuk menentukan persamaan garis singgung parabola di titik (x1, y1) yang
terletak pada parabola, pertama kita pandang parabola dalam bentuk y2 = 4cx dan
rumus persamaan garis singgung yang ada rumus (2) pada seksi 6.5.1.
Menurut (2), persamaan garis singgung parabola y2 = 4cx dengan kemiringan
m adalah y = mx +
c
. Jika titik (x1, y1) merupakan titik singgung garis pada
m
parabola, maka akan berlaku
y1 = mx1 +
c
m
(1)
Sekarang nilai m akan kita cari dalam bentuk x1, y1 dan c yang mana
parameter itu sudah diketahui/diberikan.
Kalikan masing-masing ruas pada persamaan (1) dengan m diperoleh bentuk
persamaan kuadrat
x1m2 – y1m + c = 0
6.5. Persamaan Garis Singgung Parabola  221
BAB 6 Parabola
yang memberikan penyelesaian untuk m
m=
y1  y12  4 x1c
2 x1
(2)
Karena titik (x1, y1) juga terletak pada parabola maka juga berlaku hubungan
y12 = 4cx1
(3)
sehingga jika disubstitusikan ke persamaan (2) diperoleh
m=
y1
2x1
(4)
Jika nilai m disubstitusikan ke persamaan garis singgung diperoleh
y = mx +
c
.
m
y =
2x c
y1
x+ 1
2x1
y1
y1y =
y12
x + 2x1c
2x1
Substitusi nilai y12 = 4cx1 ke persamaan di atas diperoleh
y1y = 2c(x + x1)
6.5. Persamaan Garis Singgung Parabola  222
BAB 6 Parabola
Jadi jika P(x1, y1) titik pada parabola y2 = 4cx, maka persamaan garis singgung
parabola di titik P diberikan oleh persamaan
y1y = 4c½(x + x1)
(5)
Misalkan P(x1 , y1) titik pada parabola (y – k)2 = 4c(x – h), maka persamaan
garis singgung parabola di titik P dapat dicari dari persamaan (5) dengan
mentranslasikan sumbu-sumbu koordinat sedemikian hingga titik asal (0, 0) menjadi
titik dengan koordinat (h, k), yaitu dengan substitusi
(y1 – k)(y – k) = 4c(½(x + x1) – h)
(6)
Jika parabola dalam bentuk umum Cy2 + Dx + Ey + F = 0, maka persamaan
garis singgung parabola yang menyinggung di titik P(x1, y1) dapat dituliskan dalam
bentuk:
Cy1y + ½D(x + x1) + ½E(y + y1) + F = 0
(7)
Contoh 1:
Tentukan persamaan garis singgung parabola y2 = 8x di titik yang mempunyai
ordinat 4.
Jawab:
Kita nyatakan parabola dalam bentuk baku
6.5. Persamaan Garis Singgung Parabola  223
BAB 6 Parabola
y2 = 8x

y2 = 42x
Dari persamaan di atas terlihat bahwa c = 2 dan puncak parabola di titik (0, 0)
Untuk menentukan koordinat titik yang terletak pada parabola dengan ordinat 4,
kita masukkan y = 4 pada parabola maka diperoleh absis
42 = 8x

x =2
Jadi titik singgung yang dimaksud adalah (2, 4). Dengan mempergunakan
persamaan (5) kita peroleh
4y = 22(x + 2)


4y = 4x + 8
x–y+2 =0
Grafik persamaan parabola dan garis singgungnya dapat dilihat di gambar 6.10
berikut
6.5. Persamaan Garis Singgung Parabola  224
BAB 6 Parabola
Gambar 6.10 :
Contoh 2:
Tentukan persamaan garis singgung parabola y2 – 4y – 8x + 28 = 0 di titik yang
mempunyai ordinat 6.
Jawab:
Kita nyatakan parabola dalam bentuk baku
y2 – 4y – 8x + 28 = 0

y2 – 4y = 8x – 28

y2 – 4y + 4 = 8x – 28 + 4

(y – 2)2 = 8x – 24
6.5. Persamaan Garis Singgung Parabola  225
BAB 6 Parabola

(y – 2)2 = 42(x – 3)
Dari persamaan terakhir diperoleh (h, k) = (3, 2) dan c = 2.
Untuk menentukan koordinat titik yang terletak pada parabola dengan ordinat 6,
kita substitusikan y = 6 pada parabola maka diperoleh absis
(6 – 2)2 = 42(x – 3)

x =5
Jadi titik singgung yang dimaksud adalah (5, 6). Dengan mempergunakan
persamaan (6) akan diperoleh
(6 – 2)(y – 2) = 22(x + 5 – 23)

4(y – 2) = 4(x – 1)

4y – 8 = 4x – 4

x–y+1 =0
6.5.2.2. Pada parabola yang membuka ke atas/bawah
Selanjutnya kita perhatikan parabola dalam bentuk x2 = 4cy dan rumus
persamaan garis singgung yang ada rumus (5) pada seksi 6.5.1.
6.5. Persamaan Garis Singgung Parabola  226
BAB 6 Parabola
Andaikan titik P(x1, y1) pada parabola x2 = 4cy, maka berlaku
x12 = 4cy1
(1)
dan dengan mengingat persamaan garis singgung parabola yang mempunyai kemiringan
m adalah y = mx – cm2 dan titik P(x1, y1) pada garis singgung, maka berlaku
y1 = mx1 – cm2

cm2 – x1m + y1 = 0
(2)
Diperoleh penyelesaian m dalam x1, y1, dan c yaitu
m=
x1  x12  4cy1
2c
Dengan mengingat (1) maka
m=
x1
2c
(3)
Jika nilai m ini disubstitusikan ke persamaan garis singgung diperoleh
x
x 
y = 1 x – c 1 
2c
 2c 

2
4cy = 2x1x – x12
Dengan mengingat rumus (1) diperoleh
6.5. Persamaan Garis Singgung Parabola  227
BAB 6 Parabola
4cy = 2x1x – 4cy1
 y  y1 
x1x = 4c 

 2 

(4)
Jika parabola dalam bentuk umum Ax2 + Dx + Ey + F = 0, maka persamaan garis
singgung parabola yang menyinggung di titik P(x1, y1) dapat dituliskan dalam bentuk:
Ax1x + ½D(x + x1) + ½E(y + y1) + F = 0
(5)
Contoh 1:
Tentukan persamaan garis singgung parabola y = x2 – 6x + 5 di titik (2, –3).
Jawab:
Persamaan parabola di atas jika dinyatakan dalam bentuk umum akan berbentuk
x2 – 6x – y + 5 = 0
Dengan demikian diketahui bahwa A = 1, D = –6, E = –1, dan F = 5. Diketahui
pula x1 = 2, y1 = –3. Jadi menurut persamaan (5) persamaan garis yang dicari
adalah
2x – ½6(x + 2) – ½ (y – 3) + 5 = 0

2x + y – 1 = 0
6.5. Persamaan Garis Singgung Parabola  228
BAB 6 Parabola
Latihan 6 C:
Pada soal 1 – 6 tentukan persamaan garis singgung pada parabola di titik A(x1, y1)
yang diberikan dan yang mempunyai kemiringan m yang diberikan.
1. y2 = 6x,
m = 2,
A(2, 2/3)
2. x2 + 4y = 0,
m=½,
A(2, –1)
3. x + 2y2 = 1,
m = 3/4,
A(1, –1)
4. 8x2 – 3y = 0,
m = –2,
A(1/2, 4/3)
5. 2x2 + 3y – 6 = 0,
m = –3/4,
A(1, 4/3)
6. y2 + 2y + 6x + 4 = 0, m = 1,
A(–2, 4)
7. Tentukan persamaan parabola yang menyinggung garis x = 2 di titik (2, 0) dan
titik fokusnya (4, 0).
8. Puncak parabola menyinggung garis y = 2. Tentukan persamaan parabola
tersebut jika titik fokusnya (5, 2).
9. Tentukan persamaan garis singgung parabola y 2 = –16x yang sejajar garis
x – y = 3.
10. Tentukan persamaan garis singgung parabola y2 + 2y + 6x + 4 = 0 yang tegak
lurus garis x + 2y = 6.
Latihan 6 C  229
BAB 6 Parabola
11. Tentukan persamaan garis singgung parabola x2 = –8y yang memuat titik (4, 0).
12. Tentukan persamaan garis singgung parabola y 2 – 4x = 0 yang memuat titik
(–2, –1).
13. Sebuah komet mempunyai orbit berbentuk parabolik dengan matahari sebagai
fokusnya. Pada saat komet berjarak 100 juta mil dari matahari, garis yang
menghubungkan matahari dengan komet membentuk sudut 60 dengan sumbu
parabola. Tentukan jarak lintasan terdekat ke matahari perjalanan komet tersebut.
14. Misalkan V adalah titik puncak parabola y2 = 4cx, F fokus, P titik pada parabola
yang berbeda dengan V, T adalah titik potong garis singgung di titik P dengan
sumbu-x, N adalah titik potong garis normal di P dengan sumbu-x, X proyeksi
tegak lurus titik P pada sumbu-x, dan Q titik potong antara garis singgung dengan
sumbu-y (lihat gambar 6.11). Tunjukkan bahwa
(a). TF = FP
Y
(b). TV = VX
P
Q
T V F X
N
X
(c). XN = c
(d). QF  TP
Gambar 6.11 :
Latihan 6 C  230
BAB 6 Parabola
Table of Contents
6.1. Persamaan Parabola Bentuk Baku ................................................................ 195
6.2. Konstruksi Geometrik dari Parabola............................................................. 198
6.3. Aplikasi Parabola ............................................................................................. 202
Latihan 6 A. ............................................................................................................. 204
6.4. Persamaan Parabola Bentuk Umum .............................................................. 207
Latihan 6 B. ............................................................................................................. 213
6.5. Persamaan Garis Singgung pada Parabola. .................................................. 214
6.5.1. Persamaan Garis Singgung yang mempunyai kemiringan m. ................. 214
6.5.2. Persamaan Garis Singgung yang melalui titik di Parabola. ..................... 221
Latihan 6 C: ............................................................................................................. 229
Latihan 6 C  231