BILANGAN DAN SISTEM BILANGAN (aisyah)

c
BILANGAN DAN SISTEM BILANGAN
St Aisyah S
I. PENDAHULUAN
Konsep bilangan awalnya hanyalah untuk kepentingan menghitung dan
mengingat jumlah. Lambat laun setelah para ahli matematika menambah
perbendaharaan symbol dan kata tepat untuk mendefinisikan bilangan, bahasa
matematika menjadi suatu yang penting dalam setiap perubahan kehidupan.
Apalagi bilangan selalu hadir dalam setiap perkembangan teknologi, sains,
en.konomi, bahkan dalam dunia music dan hiburan
Dahulu, ketika orang primitive hidup di gua-gua dengan mengandalkan
makanannya dari tanaman dan pepohonan disekitar gua atau berburu untuk
sekali makan, kehadiran bilangan, hitung menghitung tdak terlalu di
butuhkan.Tapi tatkala mereka mulai hidup untuk persediaan makanan , mereka
harus menghitung berapa banyak ternak miliknya dan berapa banyak milik
tetangganya.maka mulailah mereka membutuhkan hitung menghitung
Pada awalnya hanya menggunakan konsep lebih sedikit atau lebih
banyak untuk melakukan perhitungn. Misalnya membandikan dua kelompok
kupu-kupu yang berbeda banyaknya, mereka hanya membandingkan sedikit
banyaknya kedua kelompok kupu-kupu tersebut. Akan tetapi kepastian jumlah
tentang milik seseoran tersebut atau milik orang lain mulai dibutuhkan sehingga
mulai mengenall dan belajar perhitungan sederhana. Mula- mula manusia
menggunakan kerikil, menggunakan simpul tali, menggunakan jari jemari atau
memakai ranting untuk menyatakan banyaknya hewan dan kawanannya. Atau
anggota keluarga yang tinggal bersamanya. Inilah dasar pemahaman tentang
konsep bilangan.Ketika seorang berpikir tentang bilangan dua maka dalam
benaknya tertananm pengertian benda sebanyak dua buah misalnya dua kupukupu.
Dengan menggunakan jari-jari, kerikil, ranting dirasakan tidak cukup
praktis, maka orang mulai berpikir untuk menggambarkan bilangan itu dalam
suatu lambang. Lambang (symbol) untuk menulis suatu bilangan yang disebut
angka.
Lambang bilangan dibuat oleh suatu suku bangsa untuk membuat sebuah
system penulisan bilangan yang berlaku untuk bangsanya seperti bangsa maya
pada 500 tahun SM, bangsa babilonia, bangsa arab, mesir kuno, ,cina kuno dan
hindu-arab kuno.bangsa romawi kuno. Bangsa Romawi menggunakan angka-
c
angka sebagai system bilangan romawi berbentul huruf-huruf seperti I, II, III, IV,
…, XX, L, C, D, M yang hingga saat ini masih di pergunakan untuk penulisan
nomor bab dalam penulisan karya ilmiah
Dalam perkembangan selanjutnya, angka hindu arab kuno ditemukan
dalam manuskrip Spanyol abad X dan menjadi cikal bakal bagi angka-angka yang
dipakai sekarang ini
II. Sistem Bilangan
Aritmetika disebut jug Ilmu hitung adalah bagian matematika yang
membahas bilangan berikut operasinya.Secara sederhana dapat dinyatakan
bahwa aritmetika adalah ilmu hitung tentang bilangan .Di pendidikan dasar
dipelajari penjumlahan (lambang “ +”), pengurangan (lambang “ – “), perkalian
(lambang” x “ atau “ .” ),pembagian (lambang” :”),perpangkatan (lambangnya
berupa besarnya pangkat dengan diletakkan secara uppercase, pangkat 2 atau
kuadrat misalnya…..2, penarikan akar (lambing” √𝑎 untuk akar pangkat dua dari
a, untuk akar pangkat n dari a dan logaritma (lambang glog a atau logg a untuk
logaritma a dengan pokok logaritma g. Disamping itu juga digunakan pasangan
kurung “(…)” untuk mengelompokkan suatu jenis operasi. Jika demikian, maka
bila ada bilangan langsung didepan atau dibelakang kurung, maksudnya
bilangan tersebut dikalikan dengan bilangan yang ada di dalam kurung. Misalnya
2(2 + 4) adalah 2 dikalikan dengan hasil penjumlahan 3 dan 4
Sistem bilangan adalah himpunan bilangan beserta operasinya yang
didefinisikan pada himpunan tersebut. Operasinya dapat unar atau binar
(biner). Operasi unar menyangkut bilangan itu sendiri (tunggal), misalnya
perpeangkatan, Operasi biner menyangkut dua bilangan dalam himpunan yang
bersangkutan.
Dalam suatu operasi bilangan yang memuat berbagai macam operasi,
telah disepakati bahwa:
(i) Untuk menandakan bahwa suatu operasi dua bilangan harus didahulukan
maka digunakan tanda kurung buka dan tutup melingkupi kedua bilangan
tersebut beserta operasinya. Jika dieprlukan maka mungkin diperlukan
lebih dari satu pasang kurung buka dan tutup, jika demikian maka
operasi di antara pasang kurung yang terdalam mendahului operasi di
dalam pasangan di luarnya.
(ii) Perkalian dan pembagian mempunyai “kekuatan” sama artinya
dioperasikan sesuai urutannya
c
(iii)
Penjumlahan dan pengurangan mempunyai “ kekuatan “ sama artinya
dioperasikan sesuai urutannya.
(iv)
Perkalian dan pembagian
lebih kuat dari penjumlahan dan
pengurangan
Pada dasarnya perpangkatan dan penarikan akar merupakan operasi
unar,yang operasinya terhadap sebuah bilangan tertentu, sehingga tidak selalu
dapat dilakukan terhadap masing-masing bilangan yang dinyatakan dalam
bentuk operasi. Jika kemudian ada yang dapat dilakukan, hal tersebut hanya
terbatas untuk operasi tertentu saja. Misalnya (3 + 4)2 ≠ 32 + 42 tetapi ( 3 x 4)2 =
32 x 42 √4 + 9 ≠ √4 + √9, tetapi √4 𝑥 9 = √4 𝑥 √9
III. Mengenal Berbagai Jenis Bilangan
Jenis
atau
macam
bilangan
berkembang
bersamaan
dengan
perkembangan jaman dan digunakan untuk mengungkapkan sesuatu.Awalnya
untuk mengungkapkan banyaknya sesuatu, oleh keperluan berikutnya,
operasinya memerlukan ungkapan-ungkapan yang lebih lanjut namun perlu juga
lebih sederhana.Demikianlah maka ungkapan yang kemudian diwujudkan dalam
berbagai lambang juga berkembang.
Dalam perkembangan selanjutnya angka Hindu – Arab kuno ditemukan
dalam manuskrip spanyol abad X dan menjadi cikal bakal bagi angka-angka yang
dipakai sekarang ini. Namun demikian pada zaman modern sekarang ini, system
penulisan bilangan yang dikenal dan dipakai oleh hampIr setiap bangsa yang ada
di dunia adalah system penulisan bilangan yang dikembangkan oleh bangsa
Arab dengan “angka Arab” angka-angka pokoknya adalah 0,1, 2, 3, 4, 5, 6, 7, 8, 9,
sedangkan angka yang lebih dari 9 ditulis dengan mengkombinasikan angkaangka pokok tadi. Misalnya bilangan sepuluh ditulis sebagai “10” yaitu
kombinasi angka 1 dan 0 denikian juga bilangan duapuluhmpat ditulis sebagai “
24”yaitu kombinasi 2 dan 4
Dari system penulisan angka tadi , kemudian orang-orang mulai memberi
nama-nama khusus terhadap bilangan tertentu yang dikembangkan oleh bangsa
Arab itu untuk kepentingan tertentu. Misalnya, untuk keperluan hitung
menghitung, maka orang mulai memerlukan “bilangan penghitung”(counting
number)” yaitu bilangan 1, 2, 3, 4, 5, …, dan seterusnya, dimana 3 titik setelah
bilangan 5 mencirikan bahwa bilangan itu masih diteruskan sampai tak ada
batasnya dengan aturan bahwa bilangan berikutnya diperoleh dengan
c
menambah 1 kepada bilangan sebelumnya.Dari perkembngan tersebut kini kita
mengenal beberapa jenis bilangan antara lain:
1. Bilangan bilangan penghitung 1, 2, 3, 4, 5, ….sekarang dikenal dengan
bilangan asli. Dan apabila dihimpun menjadi sebuah himpunan maka
disebutlah himpunan itu dengan himpunan A
2. Untuk keperluan dalam aljabar,misalnya persamaan 3x + 5 = 11, tidak
memiliki penyelesaian apabila x peubah bilangan asli , karena x yang
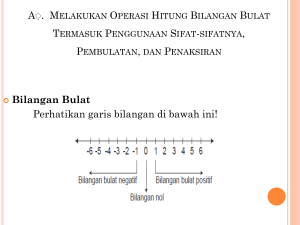
memenuhi persamaan itu adalah – 2 bukanlah bilangan asli, sehingga orangorang kemudian memperluas bilangan asli menjadi bilangan bulat.Apabila
dihimpun menjadi sebuah himunan maka disebut himpunan bilangan bulat
Bilangan bulat :{ …-3, -2, -1, 0,1, 3, ..}
3. Bilangan Cacah : 0, 1, 2, 3, ……………
4. Bilangan rasional : Bilangan yang dapat dinyatakan dalam bentuk
𝑎
𝑏
, a dan
b bilangan bulat dengan b ≠ 0. Himpunan semua bilangan rasional
𝑎
dinyatakan R = { 𝑏 ∣ a , b ∊ R dan b ≠ 0 }
8
24
6
Misalnya 17 , 57, 3 = 2
Diantara bilangan rasional ada yang merupakan bilangan bulat ada pula
yang merupakan bilangan pecah.Jika bilangan rasional bentuk decimal,
maka bagian decimal memiliki perulangan. Perulangannya merupakan
sejumlah angka tertentu atau pada 0 ( nol) contoh
1
5
1
7
= 0,200000000000000000 …
= 0,142857142857142857142857
Bilangan decimal yang berulang dengan 0, perulangannya tidak dituliskan
1
sehingga ditulis 5 = 0,2
Bagian decimal yang tidak 0 dituliskan sebagai berikut
1
7
= 0,142857142857142857142857 =0, 142857 𝑎𝑡𝑎𝑢 0,142857
Apakah setiap bilangan bulat merupakan bilangan rasional ? Jawabannya
yak arena setiap bilangan bulat dapat ditulis dalam bentuk
𝑎
𝑏
∣ a , b ∊ R dan b
≠ 0, sehingga semua himpunan bilangan bulat merupakan bagian dari
himpunan bilangan rasional atau B ⊂ R
5. Bilangan irasional :Bilangan yang muncul karena tidak ditemukannya
bentuk
𝑎
𝑏
yang dapat mewaklilinya, meskipun dalam keseharian sering
c
dijumpai.Hali ini memunculkan bilangan dengan lambang yaitu √2, yang
merupakan salah satu contoh bilangan irasional. Jika dinyatakan dalam
bentuk decimal, maka bagian desimalnya tidak pernah terjadi perulangan.
Misalnya√2 = 1,412135623730950488016887242…
√3 = 1.7320508075688772935274463415…
3
√2 = 1.2599210498948731647672106072778
6. Bilangan real, yang memuat kelima macam bilangan diatas . dituliskan
dalam himpunan bilangan Real dilambangkan dengan R
7. Bilangan Imajiner, yang muncul misalnya dengan tidak ditemukan nilai
√−1 di antara bilangan real
8. Bilangan Kompleks yang merupakan gabungan bilangan real dan
imajiner, yaitu bilangan yang berbentuk a + bi dengan a dan b bilangan
real dan I =
√−1. Bilangan real a disebut bilangan real, sedangkan
bilangan real b disebut bagian imajiner
Selain jenis-jenis bilangan diatas dikenal pula jenis bilangan lainnya, misalnya
1. Bilangan prima, yaitu bilangan asli yang memiliki tepat dua factor yang
berbeda, yaitu 1 dan bilangan itu sendiri. Contoh : 1,2,3,5,7,11,…
Beberapa bilangan prima palindrome (bilangan yang jika lambangnya
dibaca dari depan dan belakang sama dan agak khusus diantaranya
2. Bilangan komposit adalah bilangan asli bukan 1 dan bukan bilangan
prima
3. Bilangan sempurna adalah bilangan yang jumlah semua pembagiannya
kecuali dirinya sendiri sama dengan bilangan tersebut. Contoh : 6 =
1+2+3 dan 28 = 1+2+4+7+14
4. Bilangan berkekurangan adalah bilangan yang jumlah semua pembagi
kecuali dirinya sendiri kurang dari bilangan tersebut.Contoh :14 karena
1+2+7<14
5. Bilangan berkelebihan adalah bilangan yang jumlah semua pembagi
kecuali dirinya sendiri lebih dari bilangan tersebut.Contoh : 12 karena
1+2+3+4+6.12
6. Bilangan kuadrat diartikansebagai bilangan yang merupakan kuadrat
sempurnadari sebuh bilangan asli. Contih 22 = 4
7. Bilangan kubik, diartikan sebagai bilangan yang merupakan pangkat tiga
dari sebuah bilangan asli. Contoh : 23 = 8
c
8. Bilangan aljabar adalah bilangan yang merupakan akar dri suatu
persamaan suku banyak. Contoh : anxn + an-1xn-1+ an-2xn-2+…+ a2x2+ a1x+ a0
=0
9. Bilangan transendetal adalah bilangan real yang bukan aljabar. Contoh π
IV.
Sistem Bilangan Real
Jika R adalah himpuna bilangan real, maka untuk setiap a+b = c, system
bilangan real berlaku sifat t
a. Sifat tertutup (Closure) : untuk setiap a,b ∊R, jika a+b = c dan a x b = d,
maka
(i) c ∊ R dan
(ii) d ∊ R
b. Sifat Assosiatif (pengelompokan). Untuk setiap a, b, c, ∊R berlaku
(i) a + (b + c) = (a + b) + c
(ii) a x (b + c) = (a + b) x c
c. Ada elemen netral (unsure identitas), yaitu 0 (n0l)pada penjumlahan dan
1 pada perkalian .Untuk setiap a∊R maka
(i) a +0 = a = 0 +a
(ii) 1 x a = a = a x 1
d. Elemen invers (lawan). Setiap bilangan real a mempunyai invers
penjumlahan (aditif) yaitu –a (baca : negative a). dan untuk setiap a∊R
dan a≠ 0 mempunyai sebuah invers perkalian
1
𝑎
(kebalikan dari a).
e. Sifat komutatif. Untuk setiap a, b ∊R, maka berlaku
(i) a + b = b+ a
(ii) a x b = b x a
f.
Distributif perkalian terhadap penjumlahan dan pengurangan.Untuk
setiap a, b,∊R berlaku
(i) a x (b + c) = ab + ac
(ii) a x ( b – c) = ab - ac
V.
Operasi hitung Bilangan
1. Penjumlahan
Pada penjumlahan “ +” adalah lambang untuk operasi penjumlahan atau
pertambahan, sehingga kalimat matematika jumlah delapan dan lima sama
dengan 13 ditulis secara singkat dengan “ 8 + 5 = 13 ”.Tandan + mulai dipakai
c
pada abad ke -15 untuk menandai karung padi-padian atau gandum yang
melebihi besar yang ditentukan sebelumnya. Sifat-sifat operasi penjumlahan
sebagai berikut
1. Himpunan semua bilangan real tertutup terhadap operasi penjumlahan,
yaitu untuk setiap bilangan real a + b, maka a + b merupakan bilangan
real
2. Operasi penjumlahan bersifat komutatif, yaitu untuk setiap bilangan real
a dan b berlaku a + b =b +a
3. Operasi penjumlahan bersifat assosiatif, yaitu untuk setiap bilangan real
a, b dan c berlaku
a + (b + c) = (a + b) + c
4. Operasi penjumlahan berlaku Unsure identitas yaitu 0, karena setiap
bilangan real a berlaku
a+0
5. Setiap bilangan real a memiliki lawan terhadap operasi penjumlahan
yaitu (-a), karena
a + (-a) = (-a) + a = 0
2. Pengurangan
Operasi kurang adalah lawan (invers) dari operasi tambah, misalnya “ 6
dikurangi dengan 5” sama artinya dengan “ 6 ditambah dengan lawan dari 5”
sehingga 6 – 5 = 6 + (-5) = 1
Contoh 5 – 9 = 4 + (-9) = - 5
- 4 – 12 = -4 + (- 12) = - -16
8 – ( - 15) = 8 + (+15)
- 23 – (- 17) = -23 + 17 = -6
Jadi untuk setiap bilangan a dan b berlaku a – b = a + ( -b), yaitu mengurangi
dengan sebuah bilangan sama dengan menambah dengan lawan dari bilangan
itu
3. Perkalian
Perkalian adalah penjumlahan yang berulang. Maksudnya 3 x 5 sama artinya 5
+ 5 + 5 sehingga 3 x 5 = 5 + 5 + 5 , Begitu pula yang dimaksud 5 x 3 = 3 + 3 + 3
+3+3
Didalam aljabar yang dimaksud dengan 3 x a = a + a + a dapat ditulis secara
singkat dengan 3a, dalam hal ini tanda “ x” atau kali tidak ditulis lagi
Operasi perkalian memiliki sifat-sifat yaitu
1. Komutatif (pertukaran) yaitu untuk setiap bilangan real a dan b berlaku
a+b=b+a
c
2. Assosiatif ( pengelompokan ) yaitu untuk setiap tiga bilangan real a, b, c
berlaku
a + (b + c ) = (a + b) + c
3. Perkalian memiliki unsure identitas kali yaitu 1, sebab untuk setiap
bilanganreal a berlaku
ax1=1xa=a
4. Perpangkatan
Operasi perpangkatan merupakan perkalian berulang. Misalnya tulisan 2
x 2 x 2 dapat disingkat 2 3, sehingga 2 x2 x2 = 2 3. Angka 3 disebut pangkat
sedangkan angka 2 pada 2
3
disebut bilangan pokok ( bilangan yang
dipangkatkan)
Di dalam aljabar yang dimaksud p3 adalah p x p x p , sehingga p3 = p x p x
p
Karena p2 = p x p dan p5 = p x p x p x p x p sehingga p2 x p5 = (p x p) x (p x p x p x
pxp)
= p x p x p x p x p x p x p = p7
Berdasarkan penjelasan diatas, ternyata untuk bilangan – bilangan cacah
m dan n selalu berlaku am x an = am + n
5. Pembagian
Pembagian merupakan lawan dari perkalian. Maksudnya kalimat
pembagian 10 : 2 sama artinya dengan kalimat perkalian 2 x 5 = 10 atau 5 x 2 =
10
Kesimpulan
Sistem bilangan adalah himpunan bilangan beserta operasi yang
didefinisikan pada himpunan tersebut. Sistem penulisan bilangan yang dipakai
saat ini hamper dari setiap bangsa dikembangkan oleh bangsa Arab dengan
bilangan pokok 0, 1, 2, 3, 4, 5, 6,7, 8,9. Jenis bilangan dikembangkan untuk
keperluan tertentu,misalnya keperluan hitung menghitung. Dari perkembangan
tersebut maka dikenal jenis bilangan diantaranya: bilangan asali, bilangan cacah,
bilangan bulat, bilangan rasional, bilangan irrasinal, bilangan real, bilangan
imajiner, dan bilangan kompleks. Selain itu juga terdapat jenis bilangan lain
yakni bilangan prima, bilangan, komposit, bilangan sempurna, bilangan
berkekurangan, bilangan berkelebihan, bilangan kuadat, bilangan kubik,
bilangan aljabar, dan bilangan transendetal.
Pada bilangan real berlaku sifat tertutup, sifat assosiatif, sifat Komutatif,
sifat Distributif, Unsure identitas dan elemen invers. Pada bilangan real berlaku
Operasi hitung bilangan yakni penjumlahan dan pengurangan, perkalian dan
pembagian,serta perpangkata