SAP Kalkulus B - Silabus Online IAIN Antasari Banjarmasin
advertisement

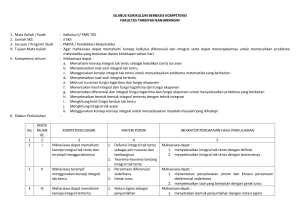
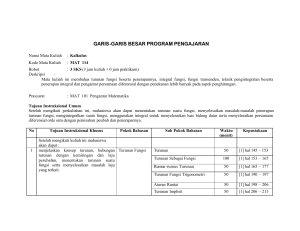
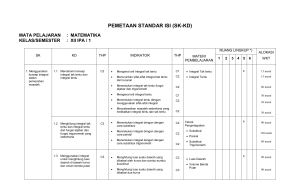
SILABUS KURIKULUM BERBASIS KOMPETENSI FAKULTAS TARBIYAH BANJARMASIN 1. 2. 3. 4. Mata Kuliah / Kode Jumlah SKS Jurusan / Program Studi Tujuan Mata Kuliah 5. Kompetensi Umum 6. Silabus Perkuliahan : : : : Kalkulus II/ PMK 705 3 SKS PMIPA / Pendidikan Matematika Agar mahasiswa dapat memahami konsep kalkulus diferensial dan integral serta dapat menerapkannya untuk memecahkan problema matematika yang berkaitan dalam kehidupan sehari-hari. : Mahasiswa dapat : a. Memahami konsep integral tak tentu sebagai kebalikan (anti) turunan b. Menyelesaikan soal-soal integral tak tentu c. Menggunakan konsep integral tak tentu untuk menyelesaikan problema matematika yang berkaitan d. Menyelesaikan soal-soal integral tertentu e. Mencari tururnan fungsi logaritma dan fungsi eksponen f. Menentukan hasil integral dari fungsi logaritma dan fungsi eksponen g. Menentukan diferensial dan integral fungsi logaritma dan fungsi eksponen untuk menyelesaikan problema yang berkaitan h. Menyelesaikan bentuk-bentuk integral tertentu dengan teknik integrasi i. Menghitung limit fungsi bentuk tak tentu j. Menghitung integral tak wajar k. Menggunakan konsep-konsep integral untuk menyelesaikan masalah-masalah yang dihadapi : 1 1 PERTE MUAN KE 2 I 2 II Mahasiswa terampil menggunakan konsep integral tak tentu 4 1. Defunisi integral tak tentu sebagai anti turunan dan lambangnya 2. Teorema-teorema tentang integral tak tentu 1. Persamaan diferensial sederhana 2. Gerak lurus 3 III Mahasiswa dapat memahami konsep integral tertentu 1. Notasi sigma sebagai penjumlahan No KOMPETENSI DASAR 3 Mahasiswa dapat memahami konsep integral tak tentu dan terampil menggunakannya MATERI POKOK INDIKATOR PENCAPAIAN HASIL PERKULIAHAN 5 Mahasiswa dapat : 1. menyelesaikan integral tak tentu dengan definisi 2. menyelesaikan integral tak tentu dengan teoremanya Mahasiswa dapat : 1. menentukan penyelesaian umum dan khusus persamaan dieferensial sederhana 2. menyelesaikan soal yang berkaitan dengan gerak lurus Mahasiswa dapat : 1. menyatakan bentuk penjumlahan dengan notasi sigma 2. Induksi matematika 3. Jumlah Reimann 4 IV Mahasiswa dapat menggunakan sifat-sifat integral tertentu 1. Luas daerah sebagai integral tertentu 2. Sifat-sifat integral tertentu 3. Teorema nilai rata-rata untuk integral 5 V Mahasiswa dapat menggunakan sifat-sifat integral tertentu 1. Teorema dasar kalkulus I 2. Teorema dasar kalkulus II 6 VI Mahasiswa dapat memahami 1. Definisi fungsi logaritma konsep turunan dan integral dari asli fungsi logaritma dan fungsi 2. Sifat-sifat fungsi logaritma eksponen serta terampil 3. Turunan fungsi logaritma menerapkannya asli 7 VII 8 VIII 9 IX Mahasiswa dapat memahami 1. Integral yang konsep turunan dan integral dari menghasilkan fungsi fungsi logaritma dan fungsi logaritma asli eksponen serta terampil 2. Definisi-definisi yang menerapkannya berhubungan dengan fungsi eksponen asli 3. Teorema-teorema untuk eksponen asli Mahasiswa dapat memahami 1. Turunan fungsi eksponen konsep turunan dan integral dari asli fungsi logaritma dan fungsi 2. Integral yang eksponen serta terampil menghasilkan fungsi menerapkannya eksponen asli Mahasiswa dapat memahami 1. Penggunaan fungsi konsep turunan dan integral dari logaritma dan fungsi fungsi logaritma dan fungsi eksponen asli eksponen serta terampil 2. Turunan dan integral dari 2. menyatakan bentuk notasi sigma menjadi bentuk penjumlahan 3. membuktikan pola/rumus matematika dengan induksi matematika 4. menghitung integral tertentu dengan jumlah Reimann Mahasiswa dapat : 1. menghitung luas daerah datar dengan integral tertentu 2. menghitung integral tertentu dengan menggunakan sifatsifatnya 3. menentukan suatu nilai pada selang tertutup dengan teorema nilai rata-rata Mahasiswa dapat : 1. menentukan turunan dari fungsi-fungsi untegral dengan menggunakan TDK I 2. menghitung integral tertentu dengan menggunakan TDK II Mahasiswa dapat : 1. menentukan fungsi logaritma asli dan pengintegralan 2. menentukan domain dan range fungsi logaritma serta menggambar grafiknya 3. menentukan turunan fungsi logaritma asli dengan menggunakan sifat-sifat kalkulus dan sifat logaritma Mahasiswa dapat : 1. menyelesaikan bentuk integral yang menghasilkan logaritma asli 2. menentukan fungsi eksponen sebagai kebalikan fungsi logaritma 3. menggambarkan grafik fungsi eksponen 4. menyelesaikan masalah yang berhubungan dengan menggunakan teorema-teoremanya Mahasiswa dapat : 1. menentukan turunan dari fungsi eksponen asli dngan sifatsifatnya 2. menentukan hasil integral yang berbentuk fungsi eksponen asli Mahasiswa dapat : 1. menyelesaikan masalah-masalah yang berhubungan dengan fungsi eksponen dan fungsi logaritma asli dalam kehidupan sehari-hari menerapkannya fungsi logaritma dan fungsi eksponen yang lain 1. Rumus-rumus dasar integral 2. Integral parsial (bagian) 10 X Mahasiswa dapat menyelesaaikan soal integral dengan menggunakan teknik integral 11 XI Mahasiswa dapat menyelesaaikan soal integral dengan menggunakan teknik integral 1. Pengintegralan fungsi trigonometri berpangkat 2. Pengintegralan dengan substitusi trigonometri 12 XII Mahasiswa dapat menyelesaaikan soal integral dengan menggunakan teknik integral 13 XIII Mahasiswa dapat menyelesaaikan soal integral dengan menggunakan teknik integral 14 XIV 15 XV Mahasiswa dapat mencari nilai limit fungsi yang berbentuk tak tentu dan mampu menghitung integral tak wajar Mahasiswa dapat menggunakan konsep-konsep integral untuk menyelesaikan masalah yang dihadapi 16 XVI 1. Pengintegralan fungsi rasional dengan pecahan parsial 2. Pengintegralan fungsi rasional dari sinus dan cosinus 1. Pengintegralan dengan bermacam-macam substitusi 2. Pengintegralan secara numeric 1. Teorema L. Hopi'tal untuk limit fungsi bentuk tak tentu 2. Integral tak wajar 1. daerah datar yang dibatasi oleh kurva-kurva 2. Volume benda yang dihasilkan dari perputaran bidang datar mengelilingi sumbu putar 3. Volume benda yang diketahui penampang irisannya 1. Panjang kuva pada suatu grafik fungsi Mahasiswa dapat menggunakan konsep-konsep integral untuk 2. menentukan turunan dan integral dari fungsi logaritma dan fungsi eksponen yang lain Mahasiswa dapat : 1. menyelesaikan soal-soal integral dengan menggunakan rumus dasar 2. menyelesaikan soal-soal integral dengan integral parsial (bagian) Mahasiswa dapat : 1. menyelesaikan soal-soal integral fungsi trigonometri berpangkat 2. menyelesaikan soal-soal integral dengan substitusi trigonometri Mahasiswa dapat : 1. menyelesaikan soal-soal integral fungsi rasional dengan pecahan parsial 2. menyelesaikan soal-soal integral fungsi rasional dari sinus dan cosinus Mahasiswa dapat : 1. menyelesaikan soal-soal dengan menggunakan bermacammacam substitusi 2. menentukan lampiran nilai integral tertentu dengan aturan trapesium Mahasiswa dapat : 1. menentukan nilai limit fungsi yang berbentuk tak tentu 2. menghitung nilai integral tertentu tak wajar Mahasiswa dapat : 1. menghitung luas daerah datar yang dibatasi oleh kurva-kurva 2. menghitung volume benda yang dihasilkan dari perputaran daerah datar mengelilingi sumbu putar 3. menghitung volume benda padat yang diketahui penampang irisannya Mahasiswa dapat : 1. menghitung panjang kurva suatu grafik fungsi antara dua menyelesaikan masalah yang dihadapi 2. Luas selimut benda 3. Titik berat bidang datar dan benda 4. Usaha 5. Tekanan zat cair 2. 3. 4. 5. 6. 7. buah titik luas selimut benda yang dihasilkan dari perpurtaran bidang datar mengelilingi sumbu putar menentukan titik berat bidang datar yang dibatasi kurvakurva menentukan titik berat volume benda yang dihasilkan bidang datar mengelilingi sumbu koordinat menentukan momen inversia bidang datar dan volume benda terhadap suatu garis menentukan usaha yang dilakukan untuk suatu kerja menentukan tekanan/gaya zat cair terhadap suatu bidang 7. Sistem Perkuliahan : - Metode yang digunakan - Bentuk Kegiatan - Evaluasi 8. Referensi : a. Buku Wajib : 1) Louis Leithold, 1986. kalkulus dan Ilmu Ukur Analitik (alih bahasa Drs. E. Hutapean). Jakarta. Penerbit Erlangga. Edisi kelima Jilid 1 dan 2 2) Purcell E. J. 1984. Kalkulus dan Geometri Analitik. (alih bahasa I Nyoman Susila dkk). Jakarta. Penerbit Erlangga. Edisi keempat Jilid 1 dan 2 b. Buku Anjuran : 1) Sallas and Hills, 1990. Calculus one and several variables. Singapore. John Willey and Sons Pullished. 2) Frank Ayres, 1972. Calculus 2 th Edition. Schawn's outline series. Mc Graw Hill Inc. Banjarmasin, Penyusun,