SISTEM PERSAMAAN LINIER (SPL) - E

SISTEM PERSAMAAN LINIER (SPL)
2.1 Persamaan Linier (PL)
Definisi 2.1.1 Persamaan Linier dengan n variabel x1, x2, …, xn
adalah suatu persamaan yang berbentuk
a1 x1 + a2 x2 + … + an xn = b,
dengan a1, a2, …, an, b bilangan riil.
Dalam suatu persamaan linier, variabel yang digunakan berderajat
nol atau satu, variabel bukan fungsi trigonometri dan tidak terjadi
perkalian antara variabelnya.
Contoh :
1. 2 x + 3y - 6z = 9 adalah suatu persamaan linier dengan 3 variabel,
2. x1 + 3x2 + 2x3 + 8x4 + 4= 0 adalah suatu persamaan linier dengan 4
variabel.
3. 6x2 + 2y – 3z = 1, bukan persamaan linier sebab memuat variable
berpangkat 2
4. 2 sin x – 3 cos x + 4 y = 5, bukan persamaan linier sebab memuat fungsi
trigonometrik
5. 6xy + 3y + z = 7 bukan persamaan linier sebab memuat hasl kali dua
variable.
Definisi 2.1.2 Selesaian (solusi) dari persamaan linier a1 x1 + a2 x2 + …
+ an xn = b adalah pasangan n-bilangan terurut (s1, s2, …, sn) yang
jika s1 disubstitusikan ke x1,
s2 disub-stitusikan ke x2, …, sn
disubstitusikan ke xn maka berlaku
a1 s1 + a2 s2 + … + an sn = b
Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)
Himpunan semua solusi dari persamaan linier a1 x1 + a2 x2 + … + an xn = b
disebut Himpunan Solisi (HS).
Contoh :
1. Persamaan 3x + 7 = 0, untuk x bilangan bulat. Maka tidak terdapat
x bilangan bulat yang memenuhi persamaan linier tersebut. Jadi,
himpunan solusinya (HS) adalah himpunan kosong. Ditulis HS = { }
2. Himpunan Solusi dari persamaan linier 2x = 8 adalah HS = {4}.
3. Himpunan Solusi dari persamaan linier 2x + 3y + z = 7 adalah HS =
{(s, t, 7-2s+3t/ s, t  R}.
4. Proses penyelesaian : Dalam HS dari persamaan linier ini, terdapat
dua variable bebas, yaitu variable x dan y. Untuk menentukan nilai
variable z, dapat ditentukan dengan mensubstitusikan variable x
dan y ke persamaan. Hasil perhitungan diperoleh nilai z = 7-2s-3t.
Jadi, HS = {(s, t, 7-2s-3t ) / s, t  R }.
( Hasil HS ini, dijelaskan pada waktu kuliah)
2.2 Sistem Persamaan Linier (SPL)
Definisi 2.2.1 Sistem Persamaan Linier (SPL) dengan n variabel x1,
x2, …, xn dan m persa-maan adalah suatu sistem persamaan yang
berbentuk
a11 x1 + a12 x2 + … a1j xj + … + a1n xn = b1
a21 x1 + a22 x2 + … a2j xj + … + a2n xn = b2
.
.
. .
. .
. .
**(1)
am1 x1 + am2 x2 + … amj xj + … + amn xn = bm
dengan aij  R,I=1,2, …, m dan j=I,2, … , n.
Definisi 2.2.2 Selesaian (solusi) dari System Persamaan Llinier (**)
adalah pasangan n-bilangan terurut (s1, s2, …, sn) yang jika s1
Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)
disubstitusikan ke x1, s2 disubstitusikan ke x2, …, sn disubstitusikan
ke xn maka berlaku ai1 s1 + ai2 s2 + … + ain sn = bi, i=1,2, …, m
Secara lengkap, jika (s1, s2, …, sn) dari SPL (**) maka (s1, s2, …, sn)
merupakan solusi dari setiap persamaan dalam SPL (**). Artinya
berlaku
a11 s1 + a12 s2 + … a1j sj + … + a1n sn = b1
a21 s1 + a22 s2 + … a2j sj + … + a2n sn = b2
.
.
. .
. .
. .
am1 s1 + am2 s2 + … amj sj + … + amn sn = bm
Himpunan semua selesaian dari Sistem Persamaan Linier (**) disebut
Himpunan Solusi
Notasinya HS
Sistem Persamaan Linier yang mempunyai selesaian disebut
Konsisten dan Sistem yang tidak mempunyai selesaian disebut tidak
konsisten
Contoh :
Diberikan suatu SPL sebagai berikut :
1. 2x + 3y =7
3x + y =7
2.
x + 2y = 5
3. 2x + 5y = 7
2x + 4y = 10
6x + 15y = 10
Penyelesaian.
Berdasarkan SPL di atas maka pasangan bilangan (2,1) merupakan
selesaian dari SPL (1) karena x=2 dan y=1 memenuhi kedua persamaan,
yaitu 2 . 2 + 3 . 1 = 7 dan 3 . 2 + 1 . 1 = 7 sehingga diperoleh HS = {
(2,1) }.
Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)
Pada SPL (2), persamaan-2 merupakan 2 kali persamaan-1 sehingga SPL
mempunyai satu persamaan dengan 2 variabel. Maka terdapat 1
variable bebas dan misal variabel bebasnya adalah y. Variabel bebas y
dapat dipilih y = t, t bilangan riil. Substitusikan y = t ke persamaan
sehingga didapat nilai x = 7-2t . Jadi HS = {(7-2t, t) / t  R}.
Pada SPL(3), tidak terdapat pasangan bilangan (x,y) yang memenuhi
kedua persamaan. Sebab, jika memenuhi persamaan 1 maka 6x + 15y =
3(2x + 5y) = 3 . 7 = 21  10, sehingga HS = { }.
Untuk melihat tafsiran geometri dari selesaian suatu SPL, diberikan
SPL dengan 2 persamaan dan 2 variabel, sebagai berikut :
a1 x + b1 y = c1
a2 x + b2 y = c2,
dengan a1, a2, b1 dan b2 konstanta riil tidak nol.
Grafik persamaan-persamaan ini merupakan garis, misal garis l1 dan
garis l2. Karena titik (x,y) terletak pada sebuah garis jika dan hanya jika
bilangan-bilangan x dan y memenuhi persamaan tersebut, maka selesaian
SPL tersebut akan bersesuaian dengan titik perpotongan dari garis l1 dan
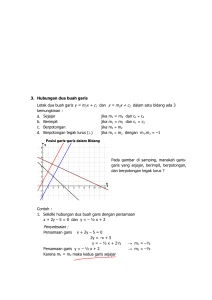
garis l2. Terdapat 3 (tiga) kemungkinan, yaitu :
(a). garis l1 dan garis l2 sejajar, yaitu jika tidak terdapat titik
perpotongan sehingga sistem tidak mempunyai selesaian
(b). garis l1 dan garis l2 berpotongan pada satu titik, sehingga sistem
hanya mempunyai satu (tunggal) selesaian.
(c). garis l1 dan garis l2 berimpit artinya terdapat takterhingga
banyak titik perpotongan. Dalam hal ini sistem mempunyai
takterhingga banyak selesaian. Biasa dikatakan SPL mempunyai
banyak solusi.
Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)
Secara visual dapat digambarkan, sebagai berikut :
Y
y
X
l1 l2
a) tidak ada solusi
y
x
l1
(b) satu solusi
l2
x
l1 dan l2
(c) takterhingga banyak solusi
Berdasarkan ilustrasi kasus di atas, maka SPL mempunyai tiga
kemungkinan yang berkaitan dengan selesaian, yaitu tidak mempunyai
selesaian, mempunyai satu selesaian dan mempunyai takterhingga banyak
selesaian.
2.3 Metode Selesaian SPL
2.3.1 Operasi Persamaan Linier (OPL)
Metode dasar untuk menyelesaikan suatu SPL adalah mengganti
sistem yang diberikan dengan sistem baru. Sistem baru yang mempunyai
himpunan selesaian (HS) sama, dengan pemecahan yang lebih mudah.
Sistem baru ini diperoleh dari suatu tahapan dengan menerapkan suatu
langkah operasi. Operasi-operasi yang dilakukan dimaksudkan untuk
menghilangkan variabel-variabel secara sistematis.
Operasi Persamaan Linier (OPL) tersebut adalah
1. mengalikan suatu persamaan dengan skalar riil tidak nol, k
2. menukar letak dua persamaan
3. mengganti suatu pers. dengan pers. tsb + k kali pers. lain
Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)
Untuk menyelesaikan suatu SPL dapat dilakukan dengan satu atau
lebih operasi persamaan linier (OPL).
Contoh : Diberikan suatu SPL dengan 3 persamaan dan 3 variabel
x + 2y + 3z = 6
2x + 3y + 2z = 7
3x + y + 2z = 6
(2)
Penyelesaian. Untuk menyelesaikan SPL di atas digunakan langkahlangkah OPL :
persamaan 2 diganti dengan persamaan-2 + (-2) kali persamaan-1,
sehingga diperoleh SPL baru, yaitu
x + 2y + 3z = 6
- y - 4z = -5
3x + y + 2z = 6
(3)
persamaan 3 pada SPL (3) diganti dengan persamaan 3 + (-3) kali
persamaan 1, sehingga diperoleh SPL baru, yaitu
x + 2y + 3z = 6
- y - 4z = - 5
- y - 7z = -12
(4)
persamaan 3 pada SPL (4) diganti dengan persamaan 3 + (-1)
persamaan 2 sehingga diperoleh SPL baru, yaitu
x + 2y + 3z = 6
- y - 4z = - 5
(5)
-3z = - 3
Berdasarkan persamaan 3 pada SPL (5), didapat z = 1. Dengan
mensubstitusikan z=1 ke persamaan 2 diperoleh -y – 4 . 1 = -5 sehingga
didapat y = 1. Kemudian, dengan mensubstitusikan z=1 dan y =1 ke
persamaan 1 diperoleh x + 2 . 1 + 3 . 1 = 6 sehingga didapat x = 1.
Dengan demikian didapat HS = { (1,1,1) }.
Create PDF files without this message by purchasing novaPDF printer (http://www.novapdf.com)