1.6. PERSAMAAN GARIS LURUS Kemiringan/Gradien Garis

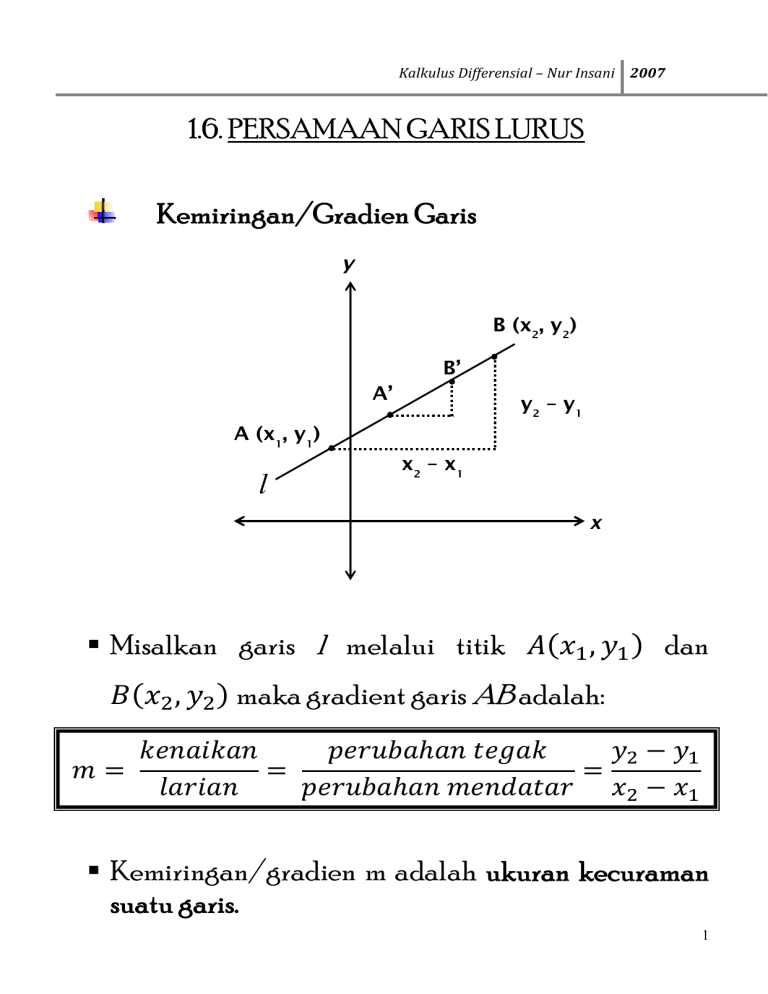
Kalkulus Differensial – Nur Insani 2007 1.6. PERSAMAAN GARIS LURUS
Kemiringan/Gradien Garis
y
B (x2, y2)
B’
A’
y2 – y 1
A (x1, y1)
x2 – x 1
l
x
Misalkan garis l melalui titik
,
,
dan
maka gradient garis AB adalah:
Kemiringan/gradien m adalah ukuran kecuraman
suatu garis.
1
Kalkulus Differensial – Nur Insani 2007 ,
Bila ada titik lain,
maka:
y
B (x2, y2)
A (x1, y1)
C (x3, y3)
l
x
Gradien garis AB
& garis AC sama!
Persamaan garis melalui titik 2,1 dgn gradient
yaitu:
1
2
2
Kalkulus Differensial – Nur Insani 2007 1
Darimana rumus tsb?
Misalkan titik
1
2
,
4
5
dan 2,1 melalui garis tsb, maka:
5
1
4
1
2 2
• Jadi, persamaan garis yg melalui titik
,
dgn gradient m:
Bentuk Kemiringan Titik
• Persamaan garis yg memotong sumbu-y di
,
dgn gradien m:
0
Bentuk Kemiringan Intersep
3
Kalkulus Differensial – Nur Insani 2007 Dari bentuk diatas, dgn segera kita dpt mengetahui
kemiringan & perpotongan garis di sumbu-y (yaitu di b,
atau dengan kata lain intersep-y b).
Persamaan Garis Tegak
y
2,3
3
2
2,1
1
1
2
k
x
tidak terdefinisi
Tetapi garis tegak tetap mempunyai persamaan, yaitu:
4
Kalkulus Differensial – Nur Insani 2007 Persamaan Garis Mendatar
y
k
3
2
1,2
3,2
1
1
2
3
x
Gradien garis l adalah:
2
3
2
1
0
2
0
Jadi, persamaan garis l yaitu:
2
0
4
2
Secara umum, persamaan garis mendatar yg melalui
0,
yaitu:
5
Kalkulus Differensial – Nur Insani 2007 • Secara umum, persamaan umum garis lurus:
0
Contoh:
1.
1
2
2.
2
2
1
0
0
• Bagaimana menentukan persamaan garis jika yg
diketahui hanya 2 titik pd garis tsb, tanpa diketahui
(gradiennya)?
¾ Tentukan gradient garis yg melalui titik
,
dan
,
:
¾ Bentuk persamaan garisnya:
6
Kalkulus Differensial – Nur Insani 2007 2
2
1
2
1
2
1
1
,
Persamaan garis yg melalui
&
,
.
Garis-Garis Sejajar
Jika dua garis sejajar
mempunyai gradien sama.
Contoh:
1.
Tunjukkan bahwa kedua garis sejajar dan
gambarlah kedua garis tsb.
3
2
3
0
6
4
5
0
2. Carilah persamaan garis yg melalui
sejajar dgn garis 4
2
1
2,3 yg
0.
7
Kalkulus Differensial – Nur Insani 2007 Garis-Garis Tegak Lurus
k
3
2,
2
2
1,
1
1
2
1
3
x
Menurut Phytagoras,
,0
,0
2 ,
2 1
8
Kalkulus Differensial – Nur Insani 2007 Jadi, dua garis saling tegak lurus
gradiennya saling
berkebalikan negative.
.
1
atau
1
9
Kalkulus Differensial – Nur Insani 2007 Problem Set # 1
1. Tentukan HP dari ketaksamaan :
a.
4
2
-3 >
-7
x
x
b.
1
≤ 4
3x - 2
2. Tentukan HP dari ketaksamaan nilai mutlak berikut :
a.
3
−4 > 2
x
b. x - 2 < 3 x + 7
3. Tentukan suatu persamaan lingkaran :
a. yang melalui tiga titik A (4 , 5), B (3 , -2) dan C (1 , -4).
b. yang berpusat di (-2 , 5) dan menyinggung garis x = 7.
c. yang menyinggung garis 3
4. Diketahui garis l dengan persamaan 2
5
0 di (-1 , 1) dan melalui titik (3 , 5).
3
4 dan titik P ( 1 , -3).
a. Tentukan suatu persamaan garis yg melalui P dan tegak lurus l.
b. Jarak terdekat dari P ke l.
5. Tentukan suatu persamaan garis yang menyinggung lingkaran
6
12
4
0 di titik (5 , 1).
10