tautologi - Staffsite STIMATA

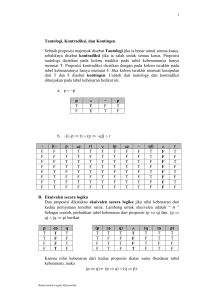
P a g e | 17
TAUTOLOGI
A.
MENGEVALUASI VALIDITAS ARGUMEN
Tabel
kebenaran
digunakan
untuk
pembuktian
validitas
argument.
Sebelum
mengevaluasi validitas suatu argument, pernyataan – pernyataan terlebih dahulu diubah
menjadi ekspresi logika. Salah satu metode yang dapat digunakan adalah teknik parsing dengan
membentuk Parse Tree.
Contoh:
1. Jika anda mengambil mata kuliah logika informatika dan jika anda tidak memahami
tautologi maka anda tidak lulus.
Misal:
P = Anda mengambil mata kuliah logika informatika
Q = Anda memahami tautologi
R = Anda lulus
Maka ekspresi logika untuk pernyataan di atas adalah
𝑃 ∧ ~𝑄
→ ~𝑅
Selanjutnya dibuat tabel kebenaran:
P
Q
R
~Q
~R
𝑷 ∧ ~𝑸
T
T
T
F
F
F
T
T
T
F
F
T
F
T
T
F
T
T
F
T
F
T
F
F
T
T
T
T
F
T
T
F
F
F
T
F
T
F
F
T
F
T
F
F
T
T
F
F
T
F
F
F
T
T
F
T
𝑷 ∧ ~𝑸
→ ~𝑹
2. Tidak belajar, tidak lulus.
Pernyataan di atas dapat diubah menjadi:
Jika anda tidak belajar, maka anda tidak lulus.
Misal:
Liduina Asih Primandari, S.Si.,M.Si
P a g e | 18
P = Anda belajar
Q = Anda lulus
Maka ekspresi logika untuk pernyataan di atas adalah
~𝑃 → ~𝑄
Selanjutnya dibuat tabel kebenaran:
P
Q
~P
~Q
~𝑷 → ~𝑸
T
T
F
F
T
T
F
F
T
T
F
T
T
F
F
F
F
T
T
T
3. Barang – barang yang dibeli di toko ini dapat dikembalikan hanya jika berada dalam
kondisi baik, dan hanya jika pembeli membawa bukti pembeliannya.
Misal:
P = Barang – barang yang dibeli di toko ini dapat dikembalikan
Q = Barang – barang dalam kondisi baik
R = Pembeli membawa bukti pembelian
Maka ekspresi logika untuk pernyataan di atas adalah
𝑃 → 𝑄∧𝑅
Selanjutnya dibuat tabel kebenaran:
P
Q
R
𝑸 ∧𝑹
𝑷 → 𝑸∧𝑹
T
T
T
T
T
T
T
F
F
F
T
F
T
F
F
T
F
F
F
F
F
T
T
T
T
F
T
F
F
T
F
F
T
F
T
F
F
F
F
T
Liduina Asih Primandari, S.Si.,M.Si
P a g e | 19
4. Jika Badu rajin belajar dan sehat, maka Badu lulus ujian, atau jika Badu tidak belajar rajin
dan tidak sehat, maka Badu tidak lulus ujian.
Misal:
P = Badu rajin belajar
Q = Badu sehat
R = Badu lulus ujian
Maka ekspresi logika untuk pernyataan di atas adalah
(𝑃 ∧ 𝑄 → 𝑅) ∨
B.
∼𝑃 ∧ ∼𝑄
→ ~𝑅
TAUTOLOGI
Suatu ekspresi logika yang selalu bernilai benar di dalam tabel kebenarannya, tanpa
memedulikan nilai kebenaran dari proposisi – proposisi di dalamnya disebut tautologi.
Contoh:
1. Apakah 𝐴 ∨ ~𝐴 adalah tautologi?
Bukti:
Tabel kebenaran 𝐴 ∨ ~𝐴
A
~A
𝑨 ∨ ~𝑨
T
F
T
F
T
T
Jadi, 𝐴 ∨ ~𝐴 adalah tautologi.
2. Apakah ~ 𝐴 ∧ 𝐶 ∨ 𝐶 adalah tautologi?
Bukti:
Tabel kebenaran ~ 𝐴 ∧ 𝐶 ∨ 𝐶
A
C
𝑨 ∧𝑪
~ 𝑨 ∧𝑪
~ 𝑨∧𝑪 ∨𝑪
T
T
T
F
T
T
F
F
T
T
F
T
F
T
T
F
F
F
T
T
Jadi, 𝐴 ∨ ~𝐴 adalah tautologi.
Liduina Asih Primandari, S.Si.,M.Si
P a g e | 20
C.
KONTRADIKSI
Suatu ekspresi logika yang selalu bernilai salah di dalam tabel kebenarannya, tanpa
memedulikan nilai kebenaran dari proposisi – proposisi di dalamnya disebut kontradiksi.
Contoh:
1. Apakah 𝐴 ∧ ~𝐴 adalah kontradiksi?
Bukti:
Tabel kebenaran 𝐴 ∧ ~𝐴
A
~A
𝑨 ∧ ~𝑨
T
F
F
F
T
F
Jadi, 𝐴 ∧ ~𝐴 adalah kontradiksi.
𝐴 ∨ 𝐶 ∧ ~𝐴
2. Apakah
∧ ~𝐶 adalah kontradiksi?
Bukti:
Tabel kebenaran
∧ ~𝐶
A
C
~𝑨
~𝑪
𝑨∨𝑪
𝑨 ∨ 𝑪 ∧ ~𝑨
T
T
F
F
T
F
F
T
F
F
T
T
F
F
F
T
T
F
T
T
F
F
F
T
T
F
F
F
Jadi,
D.
𝐴 ∨ 𝐶 ∧ ~𝐴
𝐴 ∨ 𝐶 ∧ ~𝐴
𝑨 ∨ 𝑪 ∧ ~𝑨
∧ ~𝑪
∧ ~𝐶 adalah kontradiksi.
CONTINGENT
Suatu ekspresi logika yang mempunyai nilai benar dan salah di dalam tabel
kebenarannya, tanpa memedulikan nilai kebenaran dari proposisi – proposisi di dalamnya
disebut contingent.
Liduina Asih Primandari, S.Si.,M.Si