materi+pelatihan+pasca+2012
advertisement
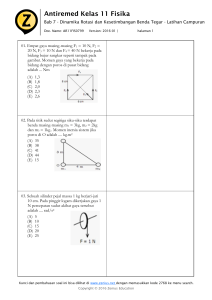
MATERI PELATIHAN GURU FISIKA SMA/MA a. Judul: Pembelajaran Gerak Rotasi dan Keseimbangan Benda Tegar Berbasis Koop untuk Meningkatkan Pemahaman Konsep Siswa SMA b. Kompetensi Dasar Setelah berpartisipasi dalam pelatihan ini diharapkan : 1) Para guru mampu memberikan inovasi pembelajaran untuk materi Gerak Rotasi dan Keseimbangan Benda Tegar untuk menciptakan pembelajaran yang menyenangkan 2) Implementasi pembelajaran mampu meningkatkan pemahaman konsep siswa tentang materi Gerak Rotasi dan keseimbangan benda Tegar c. Peta Konsep Rotasi benda tegar pengertian kinematika Sudut dan jarak Momentum sudut Kecepatan sudut torka Percepatan sudut Kekekalan momentum sudut Energi kinetik usaha d. Kata Kunci Rotasi benda tegar, sudut, jarak, kecepatan sudut, momentum sudut, torka, energi kinetik, usaha e. Strategi Pembelajaran Model : Diskusi dan kerja kelompok Metode : Diskusi Kelompok dan Pemacahan Masalah f. Media Pembelajaran : Power Point dan Animasi (Video) tentang Gerak Rotasi dan Keseimbangan Benda Tegar g. Materi Pembelajaran 1. Pengertian Benda tegar adalah sistem partikel yang mana posisi relatif partikel-partikelnya,satu dengan yang lainnya di dalam sistem, (dianggap) tetap. Akibatnya ketika benda ini berotasi terhadap suatu sumbu tetap, maka jarak setiap partikel dalam sistem terhadap sumbu rotasi akan selalu tetap. 1 Tinjau rotasi sebuah partikel dalam lintasan lingkaran dengan jejari r. Jarak yang telah ditempuh dalam selang waktu οt adalah s terkait dengan sudut ο± (dalam radian). Hubungan s dan ο± diberikan oleh s = rο±. Untuk selang waktu yang sangat kecil maka besar kecepatan linier diberikan oleh: Δπ Δπ‘ Δπ = π Δπ‘ 2. Kecepatan sudut ππ Besaran ο· ≡ ππ‘ ≡ disebut sebagai kecepatan sudut, yang arahnya diberikan oleh arah putar tangan kanan, tegak lurus bidang lingkaran. Jadi hubungan antara kecepatan linier dengan kecepatan sudut diberikan oleh π£β = π βββββπ₯ πβ 3. Percepatan Sudut Percepatan sudut ο‘ didefinisikan sebagai laju perubahan kecepatan sudut terhadap waktu ο‘≡ ππ ππ‘ Hubungan antara percepatan linier dan percepatan sudut diberikan oleh ππ£ ππ‘ ππ = r ππ‘ = ππΌ 4. Kinematika rotasi Karena persamaan-persamaan kinematika yang menghubungkan ο±, ο· dan ο‘ bentuknya sama dengan persamaan-persamaan kinematika gerak linear, maka dengan memakai analogi ini akan diperoleh kaitan sebagai berikut untuk keceptan sudut konstan π(π‘) = ππ + ππ‘ dan kaitan-kaitan berikut untuk percepatan sudut konstan 1 π(π‘) = ππ + ο·π π‘ + πΌπ‘ 2 2 π(π‘) = ππ + πΌ π‘ π(π‘)2 = ππ 2 + 2πΌπ 2 5. Momentum sudut Untuk memudahkan penyelidikan dan analisa terhadap gerak rotasi, didefinisikan beberapa besaran sebagai analog konsep gaya dan momentum. Pertama didefinisikan konsep momentum sudut π Momentum sudut suatu partikel yang memiliki momentum linear πβ dan berada pada posisi πβ dari suatu titik referensi O adalah ββπ = πβββ × πβ Perlu diperhatikan bahwa nilai l bergantung pada pemilihan titik referensi O, nilainya dapat berubah bila digunakan titik referensi yang berbeda. 6. Torka Laju perubahan momentum sudut terhadap waktu didefinisikan sebagai besaran torka πβ ππ π = (πβ π₯ πβ) ππ‘ ππ‘ ππβ = ππ‘ x πβ + πβ x ππβ ππ‘ Karena bentuk ππβ ππ‘ Maka x πβ = π£β x ππ£β = 0 ππβ πβββ = πβ x πΉβ = ππ‘ 7. Sistem partikel (rotasi) Untuk suatu sistem banyak partikel total momentum sudutnya diberikan oleh denganββββ ππ adalah momentum sudut partikel ke-i. Total torka yang bekerja pada sistem ini 3 8. Torka internal dan eksternal Torka yang bekerja pada sistem dapat dikelompokkan menjadi dua jenis, torka internal yang bekerja pada partikel oleh partikel lain dalam sistem, dan torka eksternal yang berasal dari gaya eksternal. Karena prinsip aksi-reaksi, dan bila garis kerja gaya aksi-reaksi tersebut segaris maka total torka antara dua partikel i dan j 9. Kekekalan momentum sudut Sehingga total torka yang bekerja pada sistem partikel hanyalah torka eksternal, dan perubahan momentum sudut total sistem hanya bergantung pada torka eksternal Ketika tidak ada torka eksternal maka momentum sudut total sistem akan konstan. 10. Energi Kinetik Rotasi Kita tinjau suatu sistem partikel yang berotasi terhadap suatu sumbu tetap. Jarak setiap partikel terhadapa sumbu rotasi selalu tetap. Bila sistem partikel ini adalah benda tegar maka kesemua partikel akan bergerak bersama-sama dengan kecepatan sudut yang sama. Energi kinetik sistem partikel tersebut adalah Besaran yang ada dalam tanda kurung didefinisikan sebagai momen inersia I dari sistem relatif terhadap sumbu rotasi Bila bendanya kontinum, maka perumusan momen inersianya menjadi dengan π!2 adalah jarak tegak lurus elemen massa dm ke sumbu putar 4 11. Teorema sumbu sejajar Tinjau sebuah benda seperti tampak pada gambar di bawah ini dengan titik pm adalah titik pusat massanya. Momen inersia bendaterhadap sumbu di titik P dan momen inersia terhadap sumbu yangsejajar tetapi melalui titik pusat massanya terkait sebagai berikut Tetapi Sehingga suku pertama tidak lain adalah (M adalah massa total benda), suku kedua adalah momen inersia terhadap pusat massa, sedangkan suku ketiga lenyap (karena tidak lain adalah posisi pusat massa ditinjau dari pusat massa). Sehingga 12. Teorema sumbu tegak lurus Tinjau benda pada gambar di bawah iniKita ketahui bahwa 5 Jadi momen inersia terhadap suatu sumbu sama dengan jumlah momen inersia terhadap dua sumbu yang saling tegak terhadapnya 13. Usaha Definisi usaha untuk gerak rotasi sama dengan definisi usaha pada gerak linear. Sebuah partikel diberi gaya πΉβ . Partikel itu bergerak melingkar dengan lintasan yang berjejari r, menempuh lintasan sepanjang ππ β. Usaha yang dilakukan πΉβ adalah ππ = πΉβ . ππ β ββββπ₯ πβ , sehingga ππ = πΉβ . ππβ π₯ πβ = πβπ₯ πΉβ . ππβ = πβ. ππβ Tetapi kita dapat menuliskan ππ β = ππ Tetapi usaha yang dilakukan sama dengan perubahan energi kinetik, sehingga Dengan ππ=πΌππ‘ dan ππ= πππ‘, maka , maka kita peroleh πβ = πΌπΌβ 14. Kesetimbangan Benda Tegar Sebuah benda tegar berada dalam keadaan seimbang mekanis bila, relatif terhadap suatu kerangka acuan inersial a Percepatan linier pusat massanya nol. b Percepatan sudutnya mengelilingi sembarang sumbu tetap dalam kerangka acuan ini juga nol. Syarat Kesetimbangan ο· Persyaratan pertama ekuivalen dengan persyaratan bahwa total gaya eksternal yang bekerja pada benda tegar sama dengan nol πΉβ eks = 0 ο· Sedangkan persyaratan kedua ekuivalen dengan persyaratan bahwa total torka eksternal yang bekerja pada benda tegar sama dengan nol πβeks = 0 6 h. Latihan Soal dan Pembahasan 1. Sebuah cakram berputar dengan percepatan angular konstan α = 2 rad/s 2. Jika cakram mulai dari keadaan diam, berapa putara yang dibuat dalam 10 s? Pembahasan Persoalan ini adalah analog dengan persoalan linier untuk mencari jarak yang ditempuh partikel dalam suatu waktu tertentu jika benda mulai dari keadaan diam dengan percepatan konstan. Jumlah putaran dihubungkan dengan perpindahan angular dari difinis bahwa tiap putaran adalah perpindahan angular sebesar 2π rad. Jadi, kita perlu mencari perpindahan angular θ – θ 0 dalam radian untuk waktu10 s da mengalikannya dengan faktor konversi (1 put)/(2π rad). Kita tahu ω0 = 0 (cakram mulai dari keadaan diam). Jadi, θ − θ0 = θ0 t + 1 2 αt 2 = 0 + 1 (2 2 rad/s2 )(10 s)2 = 10 rad Karena itu jumlah putaran adalah 100 rad π₯ 1 putaran = 15,9 putaran 2πrad Carilah kelajua angular dari cakram pada contoh 1 setelah 10 s. Kita dapatkan π = π0 + πΌπ‘ = 0 + (2 rad/π 2 )(10 π ) = 20 rad/s Untuk memeriksa hasil ini dan juga contoh yang lalu, kita juga dapat mencari kelajuan angular: π2 = 2πΌ(π − π0 ) = 2(2 πππ/π 2 )(100 π ) = 400 πππ2 /π 2 Atau π = √400 πππ 2 π 2 = 20 πππ/π 2. Empat partikel bermassa m dihubungkan oleh batang tak bermassa hingga membentuk segi empat dengan sisi 2a dan 2b seperti ditunjukan pada gambar. Sistem berputar terhadap sebuah sumbu dalam bidang gambar yang melalui pusatnya. Carilah momen inersia terhadap sumbu ini. Dari gambar, kita dapat melihat bahwa jarak dari tiap partikel kesumbu putar adalah a. Karena itu, momen inersia tiap partikel terhadap sumbu ini dalah ma2, dan karena ada empat partikel, momen inersia total benda adalah I = 4ma2 7 Gambar Empat pertikel bermassa dihubungkan dengan oleh batag tak bermassa dan brotasi melalui sumbu yang melalui bidabg partikel-partikel itu dan melalui pusat massa Jarak b sama sekali tidak berperan karena tidak dihubungka dengan jarak dari tiap massa ke sumbu putar. 3. Sebuah tali dililitkan mengelilingi tepi cakram uniform yag diputar hingga berotasi tanpa gesekan terhadap suatu sumbu tetap yang melalui pusatnya. Massa cakram adalah 3 kg, dan jari-jarinya adalah 25 cm. Tali ditarik dengan gaya F yang besarnya 10 N (Lihat Gambar). Jika cakaram mula-mula diam berapakah kecepatan angularnya setelah 5 s? Momen inersia cakram uniform cakram terhadap sumbunya adalah 1 1 πΌ = 2 ππ 2 = 1 (3ππ)(0,25 m)2 = 9,38 π₯ 10−2 ππ π2 karena arah tali pada saat tali meninggalkan tepi cakram adalah selalu tagensial terhadap cakram. Lengan gaya yang dikerjakannya adalah R. Jadi torsi luar adalah Gambar sebuah tali yang dililitkan mengelilingi cakram. τ = FR = (10 N)(0,25 m) = 2,5 N.m untuk mendapatkan kecepatan angular, mula-mula kita harus mendapatkan percepatan angular dari hukum kedua Newton untuk gerak ∝= ππππ‘π‘π πΌ 2,5 π.π = 0,0938 πΎπ.π2 = 26,7 πππ/π 2 Karena α konstan kita dapatkan ω dari persamaan 8-8 dengan mengambil ω0 = 0 : π = π0 + πΌπ‘ = 0 + (26,7 rad/π 2 )(5 π ) = 133 rad/s 4. Sebuah benda bermassa m dikaitkan pada tali ringan yang dililitkan mengelilingi sebuah roda dengan momen inersia I dan jari-jari R (lihat gambar). Bantalan roda adalah licin, dan tali tidak selip di tepinya. Carilah tegangan tali dan percepatan benda. Satu-satunya gaya yang bekerja pada roda adalah tegangan tali T, yang mempunyai lengan R dan menghasilkan rotasi searah jarum jam. Dengan mengambil arah jarum sebagai arah positif, kita dapatkan TR = Iα Gambar sebuah tali yang dililitkan mengelilingi cakram. Dua buah gaya yang bekerja pada benda yang digantung, tegangan ke atas T dan gaya gravitasi ke bawah mg. Dengan mengambil arah ke bawah adalah positif. Agar a dan α 8 mempunyai tanda yang sama. Dari huku kedua Newton kita dapatkan mg – T = ma Ada tiga besaran yang tidak diketahui, T, a dan α dalam kedua persamaan ini. Tali merupakan kendala yang menyebabkan kita dapat menghubungkan a dan α. Karena tali tidak selip, kelajuanya sama dengan percepatan tengansial titik pada tepi roda. Jadi percepatannya adalah A = Rα Denga mensubtitusi a/R untuk α kita dapatkan π ππ = πΌ π ππ 2 πΌ π= Subtitusi hasil ini untuk adalam Persamaan 8-20 menghasilkan ππ − π = π ππ 2 πΌ Atau π (1 + ππ 2 ) = ππ πΌ πΌ = ππ πΌ + ππ 2 π= Kita dapat menggunakan untuk T dalam persamaan 8-22 untuk mendaptkan a : ππ 2 π πΌ + ππ 2 π= 5. Sebuah cakram uniform yang bermassa 3 kg dan berjari-jari 12 cm berputar 480 put/men. Hitunglah energi kinetiknya. Dari Tabel 8-1, momen inersia cakram uniform diberikan oleh 1 1 πΌ = 2ππ 2 = 2 (3 ππ)(0,12 π)2 = 0,0216 ππ. π2 Kecepatan angularnya adalah 480 ππ’π‘ππππ 2π πππ π=( )( ) = 50,3 πππ/π 60 π 1 ππ’π‘ππππ Dengan demikian, energi kinetik adalah πΎ= 1 2 πΌπ2 = 1 2 (0, ,0216 ππ. π2 ) (50,3 πππ/π )2 = 27,3 π½ 9 Perhatikan bahwa kita menghilagkan satuan tak berdimensi radian dan dan menggunakan 1 kg.m2/s2 = 1 J. 6. Mesin sebuah mobil menghasilkan torsi 380 N.m pada 3200 put/men. Hitunglah daya keluaran mesin ini. Kelajuan angular yang sesuai dengan 3200 put/men adalah 3200 ππ’π‘ππππ 2π πππ 1 πππππ‘ π=( )( )( ) = 335 πππ/π 1 πππππ‘ 1 ππ’π‘ππππ 60 π Daya keluaran mesin diberikan π = ππ(380 π. π)(335 πππ⁄π ) = 127 ππ 7. Carilah momen inersia cincin bermassa M dan berjari-jari R terhadap sumbu yang melalui pusatnya da tegak lurus bidang cincin Dalam kasus ini, semua massa berada pada jarak r = R sehigga momen inersianya adalah πΌ = ∫ π 2 ππ = π 2 ∫ ππ = ππ 2 Gambar 8-8 sebuah cincin berotasi terhadap sumbu yang tegak lurus pada bidang cincin dan melalui pusatnya. Karena semua massa cincin berada pada jarak R dari sumbu ini, momen inersianya adalah MR2 8. Carilah momen inersia sebuah batang dengan kerapatan uniform terhadap sumbu yang tegak lurus batang melalui salah stu ujungnya. Elemen massa dm ditunjukkan pada Gambar 8-9. Elemen ini berada pada jarak x dari sumbu putar. Karena massa total M didistribusikan secara uniform sepanjag L, kerapatan massa linier adalah π = π/πΏ. Jadi, ππ = π ππ₯ = (π⁄πΏ)ππ₯. Momen inersia terhadap sumbu y adalah πΏ Gambar geometri untuk menyusun integral untuk menghitung momen inersia batang terhadap sumbu yang tegak lurus batang dan memlalui salah satu ujungnya πΏ πΌπ¦ = ∫0 π₯ 2 ππ = ∫0 π₯ 2 = π ππ₯ πΏ = π πΏ 2 ∫ π₯ πΏ 0 ππ₯ π 1 3 πΏ ππΏ3 1 π₯ ∫ = = ππΏ2 πΏ 3 3πΏ 3 0 10 Momen inersia terhadap sumbu z juga 13 ππΏ2, dan momen inersia terhadap sumbu x adalah nol, jika semua massa berada pada sumbu x. 9. Carilah momen inersia cakram uniform terhadap sumbu yang melewati pusatnya dan tagak lurus bidang cakram. Kita menduga bahwa I akan lebih kecil dari pada MR2 karea massa cakram tidak terkonsentrasi di r = R seperti pada cincin, melainkan terdistribus secara uniform dari r = 0 sampai r = R. Kita harus hitung I dengan mengambil elemen massa dm yang ditunjukkan pada Gambar 8-10. Tiap elemen massa adalah sebuah cincin berjari-jari r yang tebalnya dr. Momen inersiabtiap elemen adalah r2 dm. Karena luas tiap elemen adalah dA = 2πr2 dr. Maka massa tiap elemen adalah Gambar 8-10 geometri untuk menyusun integral untuk menghitung momen inersia cakram yag uniform yang berputar tehadap sebuah sumbu yang melalui pusatnya dan tegak lurus bidang cakram. ππ = π π΄ ππ΄ = π π΄ 2π ππ 2 Dengan A= πr adalah luas cakaram, jadi kita dapatkan πΏ π πΌ = ∫ π 2 ππ = ∫ π 2 2ππ ππ π΄ 0 = 2ππ π 3 2π π 4 1 ∫ π ππ = = ππ 2 2 2 ππ 0 π 4 2 10. Soal-soal pilihan ganda 1. Sebuah mesin mobil menghasilkan daya 3π 2 π₯ 104 W ketika berputar pada laju 1800 putaran per menit. Momen gaya yang dihasilkan sebesar A. 500 N.m B. 450 N.m C. 400 N.m D. 350 N. m E. 300 N.m 2. Dua buah partikel identik masing-masing bermassa 2 kg dihubungkan oleh batang tipis tak bermassa (panjang batang 4 m). Sistem berputar pada sebuah sumbu tegak lurus batang yang berjarak 1 m dari salah satu partikel. Momen inersia sistem adalah.... A. 4 kg m2 B. 5,3 kg m2 C. 20 kg m2 D. 32 kg m2 E. 36 kg m2 11 3. Roda sepeda dengan momen inersia I = 1 kg m2 semula tidak berputar, jika sebuah torka sebesar 10 N.m bekerja padanya selama 10 s, maka kecepatan sudut setelah 10 s adalah... A. 50 rad/s B. 100π rad/s C. 100 rad/s D. 500 rad/s E. 1000 rad/s 4. Sebuah benda bermassa 1 kg diikat dengan tali sepanjang 1 m dan berputar di atas permukaan bidang yang licin dengan kecepatan sudut 0,5 rad/s. Momen gaya yang dikerahkan oleh tegangan tali adalah... A. 0 N. M B. 0,25 N. M C. 0,5 N. M D. 1,5 N. M E. 2 N. M 5. Dua beban dengan massa 5,0 kg dan 7,0 kg diletakkan dengan jarak 4,0m satu sama lain pada sebuah batang yang ringan (yang massanya dapat diabaikan). Hitung momen inersia sistem ketika dirotasikan sekitar sebuah sumbu yang berada di tengah antara kedua beban tersebut. A. 48 kg m2 B. 50 kg m2 C. 58 kg m2 D. 60 kg m2 E. 68 kg m2 11. Sumber Referensi Douglas C. Giancolli. (2001). Fisika. Edisi Kelima. Jakarta: Penerbit Erlangga Paul M. Fishbane, et. al. (Physics for Scientists and Engineers with Modern Physics Paul A. Tipler. (2000). Physics for Scientists and Engineers, 5e 12 MATERI PELATIHAN GURU FISIKA SMA/MA BIDANG FISIKA Materi Disampaikan Dalam Rangka Pelatihan Mata Pelajaran Fisika SMA/MA Program Pascasarjana UNY Bekerjasama dengan DIKTI di Hotel UNY pada Tanggal 11-13 Mei 2012 Oleh Dr. Insih Wilujeng PROGRAM PASCASARJANA UNY 2012 13 14
