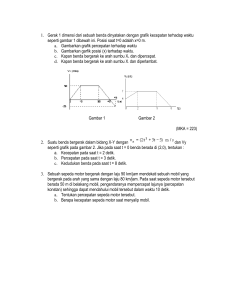
Benda pada pegas vertikal

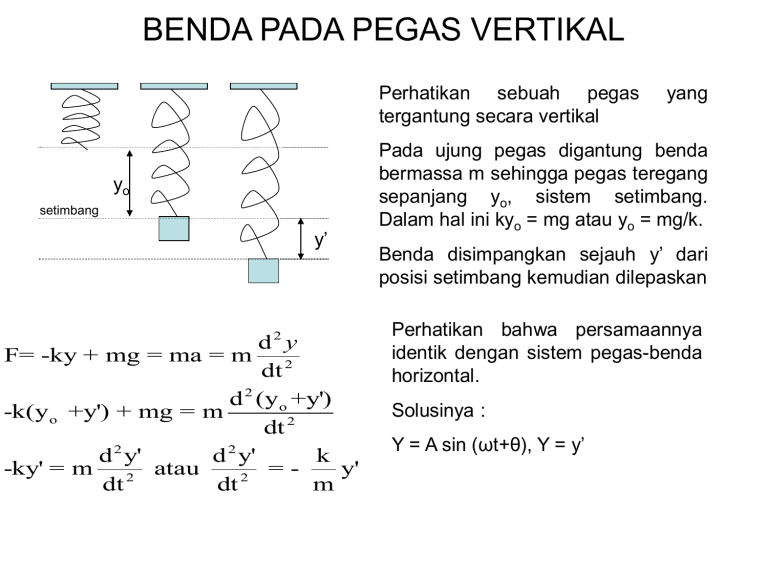
BENDA PADA PEGAS VERTIKAL
Perhatikan sebuah pegas
tergantung secara vertikal
yo
setimbang
y’
d2 y
F= -ky + mg = ma = m
dt 2
d 2 (y o +y')
-k(y o +y') + mg = m
dt 2
d 2 y'
d 2 y'
k
-ky' = m
atau
=
y'
dt 2
dt 2
m
yang
Pada ujung pegas digantung benda
bermassa m sehingga pegas teregang
sepanjang yo, sistem setimbang.
Dalam hal ini kyo = mg atau yo = mg/k.
Benda disimpangkan sejauh y’ dari
posisi setimbang kemudian dilepaskan
Perhatikan bahwa persamaannya
identik dengan sistem pegas-benda
horizontal.
Solusinya :
Y = A sin (ωt+θ), Y = y’
Contoh Soal 6.6
Benda 4 kg digantung pada sebuah pegas dengan k = 400 N/m.
a. Cari regangan pegas ketika dalam keadaan
setimbang.
b. Carilah energi potensial total termasuk energi potensial
gravitasi, ketika pegas diregangkan 12 cm.
(Asumsikan energi potensial gravitasi nol saat setimbang)
a).
m  4 kg k  400 N / m
mg 4(9,8)
yo 

 0,098 m
k
400
b).
A  0,12 m y o  0,098 m
1 2
1
E  kA  mgh  (400)(0,12) 2  4(9,8)( 0,098)  0,96 J
2
2
Contoh Soal 6.7
Benda 2,5 kg tergantung pada pegas dengan k = 600 N/m. Benda
berosilasi dengan amplitudo 3 cm. Bila benda berada pada
simpangan arah bawah maksimumnya. Cari energi potensial
sistem.
Jawab :
a).
m  2,5 kg k  600 N / m
mg 2,5(9,8)
yo 

 0,041 m
k
600
b). A  0,03 m y  0,041 m
o
1 2
1
E  kA  mgh  (600)(0,03) 2  2,5(9,8)( 0,0418)  0,906 J
2
2
Soal Latihan 6.5
Sebuah pegas dengan k = 19 N/m tergantung vertikal. Pada ujung
bebasnya diikatkan sebuah benda bermassa bermassa 0,2 kg.
dan kemudian dlepaskan. Tentukan :
a). Berapa jauh benda turun dari posisi semula [0,01 m]
b). Frekuensi [1,6 Hz]
BANDUL SEDERHANA (SIMPLE PENDULUM)
Perhatikan sebuah bandul bermassa m yang
digantungkan pada ujung tali sepanjang L,
massa tali di abaikan dan tegangan tali T.
Benda berayun ke kiri dan ke kanan mengikuti
busur lingkaran berjari-jari L. Benda setimbang
dalam arah radial T = mgcosθ.
Dalam arah tangensial bekerja gaya mgsinθ,
gaya ini selalu berlawanan arah dengan arah
perubahan θ.
d 2s
d 2 L
d 2
 F  ma   mg sin   m dt 2  m dt 2  L dt 2
d 2
   sin      g  L 2
dt
d 2 g
g



0



dt 2 L
L
T
1 2
L

 2
f

g
BANDUL FISIS (PHYSICAL PENDULUM)
Sebuah benda tegar dengan massa m
Benda dapat berputar pada titik O.
Jarak titik O ke pusat massa C adalah h.
Momen inersia benda adalah I
Gaya yang menyebabkan benda berosilasi
adalah mgsinθ dengan torka (momen gaya)
sebesar  = F R =(mg sin θ) h = mg h sin θ
Hukum Newton untuk gerak rotasi :
 = percepatan sudut [ rad/s2]
d 2
   I   mgh sin   I dt 2
d 2  mgh
mgh
  sin    



0



dt 2
I
I
I = momen inersia [kg m2]
T
 = momen gaya [N m]
R = Lengan gaya [m]
1 2
I

 2
f

mgh
BANDUL PUNTIR (TORSIONAL PENDULUM)
Bandul puntir terdiri dari benda yang
digantung pada kawat yang dipegang pada
suatu titik tetap.
Bila kawat dipuntir sebesar sudut , kawat
akan memberikan sebuah momen gaya
pemulih sebanding dengan , yaitu  = −  .
Hukum Newton untuk rotasi :
 = torka (momen gaya) [N m]
 = percepatan sudut [ rad/s2]
I = momen inersia [kg m2]
 = konstanta puntir [N/rad]
d 2
   I      I dt 2
d 2 




0



dt 2 I
I
T
1 2
I

 2
f


MOMEN INERSIA DARI BERBAGAI BENDA TEGAR
Contoh Soal 6.8
Sebuah batang bermassa m dan panjang L digantung secara vertikal pada salah satu
ujungnya. Batang berosilasi di sekitar titik setimbangnya. Berapa frekuensi sudut
osilasinya? (ω=(3g/2L)1/2)
Jawab :
1
I  mL2
3
h
1
L
2
1 
mg  L 
mgh
3g
2 




1
I
2L
mL2
3
Contoh Soal 6.9
Sebuah piringan tipis bermassa 5 kg dan jari-jari 20 cm digantung dengan suatu sumbu
horizontal tegak lurus terhadap lingkaran melalui pinggir lingkaran. Piringan
disimpangkan sedikit dari posisi setimbangnya dan dilepas. Cari frekuensi sudut
osilasinya? (ω=(200/6)1/2)
Jawab :
I  I cm  mx 2 

mgh

I
1
3
mR 2  mR 2  mR 2
2
2
mgR
2g
2(10)
200



3
3R
3(0,2)
6
mR 2
2
Soal Latihan 6.6
Sebuah batang tipis yang panjangnya 12,4 cm dan massanya 135 g
digantungkan pada suatu kawat di tengah-tengah panjangnya. Ternyata batang
ini dapat berosilasi dengan perioda 2,53 s. Kemudian suatu benda sembarang
digantungkan pada kawat yang sama dan ternyata berosilasi dengan perioda
4,76 s.
a). Berapa momen inersia dari benda sembarang tersebut ? [6,12x10-4 kgm2]
b). Berapa periodanya bila batang dan benda tersebut dijadikan satu ? [5,39 s]
Soal Latihan 6.7
Sebuah batang meteran digantungkan pada salah satu ujungnya dan berosilasi
sebagai bandul fisik.
a). Berapa periodanya ? [1,64 s]
b). Berapa panjang Lo dari suatu pendulum sederhana dengan perioda yang
sama ? [0,667 m]
Soal Latihan 6.8
Sebuah cakram berjari-jari 12,5 cm digantungkan seperti terlihat pada gambar.
Cakram ini berosilasi pada sebuah titik di tengah-tengah jari-jarinya. Bila
periodanya 0,81 s hitung berapa percepatan gravitasi di tempat tersebut. ?
[9,76 m/s2 ]