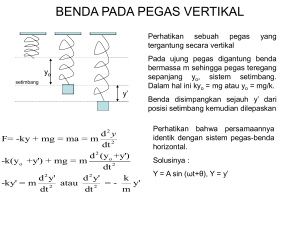
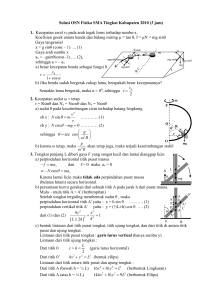
DINAMIKA PARTIKEL A. Besaran-besaran Dinamik Pada benda

RENCANA PEMBELAJARAN 3. POKOK BAHASAN: DINAMIKA PARTIKEL
A. Besaran-besaran Dinamik
Pada benda bermassa m yang bergerak dengan kecepatan ⃗, didefinisikan besaranbesaran dinamik sebagai berikut:

Momentum garis/linier (biasa disebut momentum saja) benda:
Momentum sebagai besaran vector, merupakan ukuran kuantitas gerak, yang secara
sekaligus menyatakan besar dan arah gerak benda.

Tenaga kinetik/gerak benda
berupa besaran skalar. Persamaan (3.1) dan (3.2) menghasilkan hubungan antara
momentum ⃗ dan tenaga kinetik benda (K) dengan melibatkan massa benda (m)
sebagai

Momentum sudut benda terhadap titik asal
di mana ⃗ = vector posisi benda.
Contoh 3.1 :
Benda bermassa 2 kg pada posisi ⃗
̂
̂ bergerak dengan kecepatan ⃗
̂
Hitunglah:
a. besar momentum benda!
b. tenaga kinetik benda!
c. Momentum sudut benda!
Jawab :
a. Berdasar persamaan (3.1):
Universitas Gadjah Mada
1
.̂
Besar momentum benda adalah
b.
= 4 + 9 =13
Tenaga kinetik benda (persamaan (3.2)):
c. Dari persamaan (3.4)
B. Hukum I dan II Newton, Impuls.
Benda dalam keadaan bebas/terisolir, dalam arti tidak mengalami pengaruh dari atau
berinteraksi dengan benda-benda lain, akan mempertahankan keadaan geraknya
(geraknya akan tetap), yaitu momentum dan kecepatannya tetap/konstan, yang berarti
pula benda tetap dalam keadaan diam atau bergerak lurus beraturan. Ungkapan fakta
demikian tadi disebut hukum kelembaman atau Hukum I Newton. Sesuatu yang dapat
menimbulkan perubahan momentum benda disebut gaya/kakas (force), ⃗ . Jika benda
bermassa m mengalami resultan gaya ⃗ ( ⃗
∑ ⃗ ), maka momentum benda akan
berubah mengikuti hubungan
“Laju perubahan momentum terhadap perubahan waktu sama dengan resultan gaya
yang dialami/diderita oleh benda tersebut”. Fakta yang diungkapkan oleh persamaan
(3.5) disebut Hukum II Newton atau hukum gerak Newton. Mengingat persamaan
(3.1), persamaan (3.5) dapat ditulis menjadi
yang untuk benda/sistem dengan massa konstan (m = 0) menjadi
Persamaan (3.6) atau (3.7) biasa disebut persamaan differensiaI gerak, yakni
persamaan gerak dalam bentuk persamaan differensial. Persamaan (3.7) menunjukkan
bahwa tipe/jenis gerak benda yang diungkapkan oleh ⃗
⃗
, tergantung pada resultan
gaya yang dialami oleh benda yang bersangkutan, yaitu bahwa ⃗
merupakan
penyelesaian dari persamaan differensial tersebut.
Universitas Gadjah Mada
2
Sebagai contoh:

Jika ⃗ konstan dan sejajar kecepatan ( ⃗), maka benda akan menjalani gerak lurus
berubah beraturan.

Jika ⃗ konstan dan tidak sejajar ⃗ , maka benda akan menjalani gerak parabola.

Jika ⃗ selalu tegak lurus ⃗ dan F konstan, maka benda akan menjalani gerak
melingkar beraturan.
Persamaan (3.5) dapat ditulis
dan dalam interval waktu dari t1 hingga t2 berlaku
Besaran ∫
⃗
disebut impuls gaya pada benda dalam interval waktu t1 sampai t2,
dilambangkan dengan ⃗ , sehingga diperoleh
Contoh 3.2:
Benda bermassa m meluncur pada bidang kasar dengan koefisien gesek antara benda
dengan bidang
pada posisi miring dengan kemiringan sebesar sudut
terhadap
horisontal (lihat gambar)! Carilah percepatan benda tersebut!
Jawab :
Resultan gaya pada benda tersebut adalah
Universitas Gadjah Mada
3
Contoh 3.3 :
Jika benda pada contoh 3.2 ditarik oleh gaya ⃗ sejajar bidang sehingga benda menaiki
bidang dengan percepatan sebesar a, hitunglah besar gaya penarik tersebut.
Jawab :
System dengan gaya-gaya yang bekerja (gaya berat sudah diuraikan) ditunjukkan oleh
gambar 3.3.
Soal-soal Latihan
3.1 Balok besi bermassa 10 kg mula-mula diam di atas lantai kasar, dengan koefisien gerak
0,4. Balok tersebut lalu ditarik dengan tali arah mendatar oleh gaya konstan sebesar 10
N selama 10s. g = 10 m/s2.
Hitungah:
a) kelajuan balok saat gaya tarik berhenti bekerja
b) Iamanya balok bergerak setelah gaya tarik tidak bekerja hingga berhenti.
3.2 Dua benda bermassa sama, 8 kg masing-masing diikatkan pada ujung-ujung sebuah tali
halus (massa diabaikan). Benda yang satu diletakkan di atas meja, dengan koefisien
Universitas Gadjah Mada
4
gesek antara meja dengan benda sebesar 0,2, sedang yang lain tergantung dengan tali
tersebut melalui tepi meja. Karena beban benda yang tergantung tadi sistem bergerak
dengan percepatan konstan (gesekan tali dengan meja diabaikan).
Hitunglah :
a) percepatan gerak benda-benda tersebut!
b) besar tegangan tali!
(g = 10 m/s2)
3.3 Seseorang bermassa 50 kg, berada di dalam lift (eskalator) yang bergerak ke atas
dengan percepatan sebesar 8 m/s2.
Hitunglah :
a) gaya normal yang dikerjakan oleh lantai eskalator pada orang !
b) pertanyaan seperti pertanyaan a) untuk eskalator bergerak ke bawah dengan
percepatan 8 rn/s2.
3.4 Ketentuan dan pertanyaan seperti soal no. 3.1, bedanya: besar gaya tidak konstan, tetapi
berubah menurut persamaan F = 10 + t (F dalam Newton, t dalam sekon)!
3.5 Sistem ketentuan dan pertanyaan seperti soal no. 3.2., bedanya : kedua benda terletak di
atas meja lalu salah satu benda ditarik oleh gaya sebesar 40 N mendatar.
Universitas Gadjah Mada
5