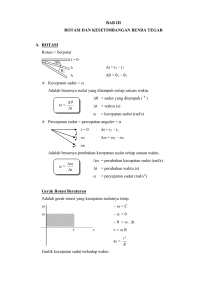
Momentum Sudut

Momentum Sudut
dimana : r3 = r4 = r5 = r6 = R sin 60o
Hukum Kekekalan Momentum
GERAK BENDA TEGAR
• Benda tegar adalah sistem benda yang terdiri atas sistem benda titik yang
jumlahnya tak-hinggadan jika ada gaya yang bekerja, jarak antara titik-titik
anggota sistem selalu tetap.
Gerak benda tegar terdiri atas
⊲ Gerak Translasi
⊲ Gerak Rotasi
⊲ Kombinasi gerak rotasi dan translasi
Gbr. Gerak rotasi dan translasi pada benda tegar
GERAK BENDA TEGAR
Kinematika Rotasi
Kinematika rotasi adalah mempelajari gerak rotasi benda tegar dengan
mengabaikan gaya penyebab gerak rotasi (lihat kinematika translasi).
Parameter fisika yang penting dalam kinematika rotasi adalah
1. Perpindahan rotasi (angular)→ θ(rad)
2. Kecepatan rotasi (angular) → ω(rad/s)
3. Percepatan rotasi (angular) → α(rad/s2)
Gerak rotasi dapat dibedakan yaitu :
1. Gerak rotasi beraturan
ω = tetap atau
α=0
2. Gerak rotasi berubah beraturan
α 0 → α > 0 atau
α < 0 dan ω > 0
artinya ada gerak rotasi dipercepat atau diperlambat.
Gerak rotasi dapat dibedakan yaitu :
1. Gerak rotasi beraturan
ω = tetap atau
α=0
2. Gerak rotasi berubah beraturan
α 0 → α > 0 atau
α < 0 dan ω > 0
artinya ada gerak rotasi dipercepat atau diperlambat.
Kecepatan dan percepatan angular sebagai vektor
ω
v
v
r
Dalam notasi vektor dengan sistem koordinat polar, gaya sentripetal dapat
dituliskan sebagai :
Vektor-vektor sesaat gaya sentripetal
adalah vektor satuan dalam arah radial, yang umumnya dipilih bernilai positif
mengarah ke luar lingkaran
Perkalian vektor
Perkalian vektor adalah operasi perkalian dengan dua operand (obyek yang
dikalikan) berupa vektor. Terdapat tiga macam perkalian vektor, yaitu
perkalian titik (dot product), perkalian silang (cross product) dan perkalian
langsung (direct product).
Perkalian titik
Perkalian titik dua buah vektor akan menghasilkan sebuah skalar. Jenis
perkalian ini bersifat komutatif.
Untuk vektor satuan terdapat hubungan-hubungan yang khusus dalam
operasi perkalian titik, yang merupakan sifat-sifat yang digunakan dalam
perkalian titik, yaitu
dan
Perkalian silang
Hasil suatu perkalian silang dua buah vektor adalah juga sebuah vektor.
Perkalian silang bersifat tidak komutatif.
Untuk vektor-vektor satuan terdapat pula hubungan yang mendasari operasi
perkalian silang, yaitu
dan
Perkalian langsung
Hasil perkalian langsung dua buah vektor adalah sebuah tensor atau matriks.
Perkalian ini tidak bersifat komutatif
Perkalian langsung dua buah vektor satuan tidak memiliki hubungan yang khusus
Besaran gerak lurus dan melingkar
Gerak lurus
Besaran
poisisi
Gerak melingkar
Satuan (SI)
m
Besaran
Satuan (SI)
sudut
rad
kecepatan
m/s
kecepatan sudut
rad/s
percepatan
m/s2
percepatan sudut
rad/s2
-
-
Perioda
T
s
-
-
Radius
R
m
HUBUNGAN GERAK TRANSLASI DENGAN GERAK ROTASI
Gerakan Translasi
Gerak Rotasi
Pergeseran
Sudut
Pergeseran Linier
S
Kecepatan Linier
v = ds/dt
Kecepatan Sudut
Percepatan Linier
a = dv/dt
Percepatan
Sudut
Gaya
Energi Kinetik
F = m.a
Ek = ½ m v2
Hubungannya
Momen Gaya
(Torsi)
Energi Kinetik
S=
w = d /dt
= dw/dt
=I
v=w.R
a=
.R
=F.R
Ek = ½ I w2
Daya
P = F.v
Daya
P=
Momentum Linier
P = m.v
Momentum
Sudut
L=PR
Usaha
W = F.s
Usaha
W=
keterangan yg perlu diperhatikan
W = usaha
W = kecepatan sudut
W2 = maksudnya dikuadratkan
.R
w
L=PR
-
Rotasi v.s. Linier
Angular
Linier
= constant
a
=
v = v 0 + at
=
0
0
+ t
constan t
1 2
x = x0 + v 0 t + at
2
1 2
+ 0t +
t
2
Untuk suatu titik pada jarak R dari sumbu rotasi:
x= R
v= R
a= R
Contoh:
Sebuah roda berputar dengan kecepatan angular awal 0 = 500 rad/s.
Pada t = 0 ia mulai melambat dengan laju 0.5 rad/s2. Berapa lama
waktu yang diperlukan untuk berhenti?
l
Ingat bahwa
l
Pakai
l
t pada
= - 0.5 rad/s2.
t
0
=0:
t
l
untuk memperoleh
Sehingga
t
0
500 rad / s
0.5 rad / s
2
1000 s 16.7 min