Algoritma

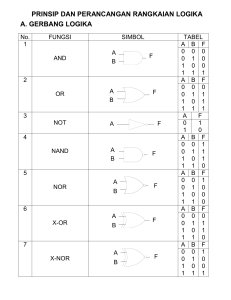
SISTEM DIGITAL
BAB 2 : GERBANG LOGIKA & ALJABAR BOOLE
16
BAB 2
GERBANG LOGIKA & ALJABAR BOOLE
Gerbang Logika (Logical Gates) atau gerbang digital merupakan komponen dasar
elektronika digital. Berbeda dengan komponen elektronika analog yang mempunyai tegangan
input dan outputnya bervariasi nilainya, maka tegangan input dan output pada komponen
digital hanya mempunyai 2 keadaan yaitu tegangan tinggi dan rendah (biasanya +5 Volt dan 0
Volt). Dalam bentuk bilangan biner keadaan pada tegangan tinggi dilambangkan dengan bit 1
sedangkan tegangan rendah dengan bit 0.Gerbang logika dasar terdiri dari gerbang Inverter,
AND, dan OR, sedangkan gerbang logika lanjut terdiri dari gerbang NAND, NOR, EXOR,
dan EXNOR. Dikatakan lanjut karena sebenarnya gerbang digital lanjut dapat dibentuk dari
beberapa gerbang digital dasar, tetapi untuk mempermudahnya dilambangkan dengan suatu
gerbang digital yang baru. Perbedaan gerbang logika ditunjukkan oleh perbedaan outputnya
pada setiap saat yang tergantung pada input yang diberikan pada saat itu. Jumlah input setiap
gerbang minimal 2 buah, hanya inverter yang mempunyai input 1 buah. Untuk menunjukkan
output dari gerbang digital berdasarkan inputnya, maka digunakan tabel kebenaran. Tabel 2.1
menunjukkan jenis gerbang logika, simbol dan tabel kebenarannya.
2.1 Gerbang Logika Dasar
2.1.1 Inverter
Sesuai dengan namanya inverter yang artinya pembalik, maka gerbang ini berfungsi
untuk membalik inputnya. Karena data digital hanya 2 macam yaitu 1 dan 0, jika inputnya 1
maka outputnya 0 dan jika inputnya 0 maka outputnya 1.
2.1.2 AND
Jika salah satu input gerbang AND bernilai 0 maka outputnya 0, dengan demikian
outputnya akan bernilai 1 hanya jika seluruh inputnya bernilai 1
2.1.3 OR
Untuk gerbang OR, jika salah satu inputnya bernilai 1 maka outputnya bernilai 1.
Output akan bernilai 0 jika seseluruh inputnya bernilai 0.
2.2 Gerbang Logika Lanjut
2.2.1 NAND
NAND singkatan dari Not AND yang berarti outputnya merupakan output dari
gerbang AND yang kemudian dibalik. Atau secara singkat dapat dikatakan output gerbang
NAND merupakan kebalikan dari gerbang AND.
2.2.2 NOR
Sama seperti gerbang NAND yang merupakan kebalikan dari gerbang AND, maka
gerbang NOR (Not OR) juga merupakan kebalikan dari gerbang OR. Jika salah satu input
gerbang NOR bernilai 1 maka outputnya akan bernilai 0.
17
SISTEM DIGITAL
BAB 2 : GERBANG LOGIKA & ALJABAR BOOLE
2.2.3 EXOR
Gerbang EXOR (atau XOR) disebut juga Paritas Ganjil yang artinya jika banyaknya
input yang bernilai 1 berjumlah ganjil maka outputnya bernilai 1.Contohnya, gerbang EXOR
3 input pada suatu saat diberikan input bernilai 1011 maka outputnya akan bernilai 1 karena
banyaknya input yang bernilai 1 ada 3 buah (ganjil).
2.2.4 EXNOR
Output gerbang EXNOR (Paritas Genap) merupakan kebalikan dari gerbang EXOR.
Jika banyaknya input bernilai 1 berjumlah genap, maka outputnya akan bernilai 1
Tabel 2.1. Tabel Kebenaran Gerbang Digital
NAMA
Inverter
AND
SIMBOL
A
Y
A
Y
B
OR
A
Y
B
NAND
A
Y
B
NOR
A
Y
B
XOR
A
Y
B
XNOR
A
Y
B
TABEL
KEBENARAN
A Y
0
1
1
0
A
0
0
1
1
B
0
1
0
1
Y
0
0
0
1
A
0
0
1
1
B
0
1
0
1
Y
0
1
1
1
A
0
0
1
1
B
0
1
0
1
Y
1
1
1
0
A
0
0
1
1
B
0
1
0
1
Y
1
0
0
0
A
0
0
1
1
B
0
1
0
1
Y
0
1
1
0
A
0
0
1
1
B
0
1
0
1
Y
1
0
0
1
SISTEM DIGITAL
BAB 2 : GERBANG LOGIKA & ALJABAR BOOLE
2.3
18
Aljabar Boole
Aljabar Boole merupakan aljabar yang digunakan di dalam sistem digital. Aljabar
Boole terdiri dari sebuah himpunan yang anggotanya terdiri dari 1 dan 0, sebuah himpunan
operator, dan sejumlah aksioma yang tidak perlu dibuktikan atau postulat.
2.3.1 Postulat Aljabar
Postulat merupakan asumsi dasar yang mendasari terciptanya : aturan, teorema, dan
properti dari sistem. Postulat yang biasanya digunakan untuk memformulasikan struktur
aljabar adalah sbb :
1. Bersifat tertutup
Suatu operator dikatakan bersifat tertutup jika untuk setiap variabel pada operasi
aritmatika tersebut merupakan anggota himpunan S.
Contoh :
S  0,1,2,3,4,5
z  x y
Jika : x = 2 ; y = 1

x,y  S
Maka : z = 2 + 1
z=3

zS
Jadi operator + bersifat tertutup
2. Hukum asosiatif
x  y z  x   y  z  untuk setiap
x, y, z  S
3. Hukum komutatif
x y  yx
untuk setiap
x, y  S
4. Elemen identitas (e)
e x  xe  x
untuk setiap
xS
Elemen identitas untuk penjumlahan (+) adalah 0 karena,
x0  0 x  x
dan elemen identitas untuk perkalian (x) adalah 1 karena,
x 1  1  x  x
5. Bersifat kebalikan (inversi)
x y  e
6. Bersifat distributif
x  ( y  z)  ( x  y)  ( x  z)
19
SISTEM DIGITAL
BAB 2 : GERBANG LOGIKA & ALJABAR BOOLE
Dari 6 buah postulat Aljabar di atas maka dapat diturunkan ketentuan-ketentuan untuk
Penjumlahan dan Perkalian pada aljabar
-
Operator Biner untuk Penjumlahan (OR) : +
Elemen Identitas untuk Penjumlahan : 0
Kebalikan Penjumlahan : Pengurangan
Operator Biner untuk Perkalian (AND) : .
Elemen Identitas untuk Perkalian : 1
Kebalikan Perkalian : Pembagian
Hukum Distributif :
a.(b  c)  (a.b)  (a.c)
2.3.2 Postulat Hantington
Postulat Hantington direpresentasikan dalam 2 bagian. Bagian yang satu dapat
diperoleh dari bagian lainnya jika operator biner (penjumlahan dan perkalian) dan elemen
identitasnya (1 dan 0) saling dipertukarkan. Properti ini disebut sebagai prinsip dualitas.
1. a. Bersifat tertutup terhadap operasi +
b. Bersifat tertutup terhadap operasi .
2. a. Elemen Identitas untuk penjumlahan : 0
b. Elemen Identitas untuk perkalian : 1


x0  0 x  x
x.1  1.x  x
3. a. Bersifat Komutatif untuk penjumlahan
b. Bersifat Komutatif untuk perkalian


x y  yx
x. y  y.x
4. a. Bersifat Distributif untuk penjumlahan
b. Bersifat Distributif untuk perkalian


x.( y  z )  ( x. y )  ( x.z )
x  ( y.z )  ( x  y ).( x  z )
5. Untuk setiap elemen x  B ada elemen x’  B (x’ : komplemen x) sehingga didapat
a. x  x' 1
b. x.x'  0
6. Ada 2 elemen : x,y  B dimana x ≠ y.
2.3.3 Postulat dan teorema Aljabar Boole
Postulat dan teorema yang banyak digunakan dalam aljabar boole dapat dilihat pada
tabel 2.1 di bawah ini. Teorema harus dapat dibuktikan berdasarkan postulat yang ada,
sedangkan postulat tidak perlu pembuktian.
SISTEM DIGITAL
BAB 2 : GERBANG LOGIKA & ALJABAR BOOLE
20
Tabel 2.2 Postulat dan Teorema Aljabar Boole
===================================================================
Postulat 2
a. x  0  x
b. x.1  x
Postulat 5
a. x  x  1
b. x.x  0
Teorema 1
a. x  x  x
b. x.x  x
Teorema 2
a. x 1 1
b. x.0  0

Teorema 3, involusi
a.  x  x
Postulat 3, komutatif
a. x  y  y  x
b. x. y  y.x
Teorema 4, asosiatif
a. x   y  z   x  y   z
b. x. y.z   x. y .z
Postulat 4, distributif
a. x y  z   xy  xz
b. x   y.z   x  y x  z 


Teorema 5. DeMorgan
a. x  y   xy
b.  x. y   x  y
Teorema 6, Absorbsi
a. x  xy  x
b. x.( x  y )  x
Contoh :
Pembuktian untuk teorema 1a yaitu : x + x = x
Bukti : x + x = x
= (x+x) . 1
dari postulat 2b.
= (x+x) . (x+x’)
dari postulat 5a.
= x + xx’
dari postulat 4b.
= x+0
dari postulat 5b.
= x
dari postulat 2a.
2.3.4 Minterm dan maxterm
Minterm merupakan kombinasi dari variabel biner dalam bentuk perkalian. Untuk 2
variabel x dan y, akan terdiri dari minterm x’y’, x’y, xy’, dan xy, sedangkan maxterm
merupakan kombinasi dari variabel biner dalam bentuk penjumlahan. Tabel 2.3 menunjukkan
minterm dan maxterm untuk 3 variabel beserta simbolnya. Untuk minterm disimbolkan
dengan huruf kecil sedangkan maxterm dalam huruf besar. Fungsi boole dapat juga
ditunjukkan dalam bentu penjumlahan minterm ()dan perkalian maxterm ()
Tabel 2.3. Minterm dan Maxterm
VARIABEL
x
y
z
0
0
0
0
0
1
0
1
0
0
1
1
1
0
0
1
0
1
1
1
0
1
1
1
MINTERM
Terms
Simbol
x’y’z’
m0
x’y’z
m1
x’y z’
m2
x’y z
m3
x y’z’
m4
x y’z
m5
x y z’
m6
xyz
m7
Contoh :
F ( x, y, z)   (1,4,6)  xyz  xyz  xyz
MAXTERM
Terms
Simbol
x+y+z
M0
x + y + z’
M1
x + y’+ z
M2
x + y’+ z’
M3
x’+ y + z
M4
x’+ y + z’
M5
x’+ y’+ z
M6
x’+ y’+ z’
M7
21
SISTEM DIGITAL
BAB 2 : GERBANG LOGIKA & ALJABAR BOOLE
2.4
Implementasi Fungsi Boole
Untuk menuliskan Fungsi Boole digunakan ekspresi aljabar (persamaan) yang terdiri
dari variabel dan operator logika. Selain itu fungsi Boole dapat juga dituliskan dalam bentuk
minterm atau maxterm. Dari fungsi Boole dapat diturunkan tabel kebenaran untuk fungsi
tersebut dan implementasinya dalam bentuk rangkaian digital yang terdiri dari beberapa
gerbang logika.
Contoh :
Tentukan Tabel Kebenaran dan Diagram Rangkaian digital dari Fungsi Boole berikut ini :
F1 ( x, y, z)  x. y  x' z
Tabel 2.4
x
0
0
0
0
1
1
1
1
Tabel Kebenaran F1 ( x, y, z)  x. y  x' z
y
z
x.y
x’z
F1
0
0
0
0
0
0
1
0
1
1
1
0
0
0
0
1
1
0
1
1
0
0
0
0
0
0
1
0
0
0
1
0
1
0
1
1
1
1
0
1
b. Rangkaian Digital F1 ( x, y, z)  x. y  x' z
y
x
F1=x.y+x’z
z
Gambar 2.1 Rangkaian F1(x,y,z) = x.y + x’z
2.5
Penyederhanaan Fungsi Boole
Fungsi (Persamaan) Boole dapat disederhanakan dengan menggunakan Postulat dan
teorema aljabar Boole. Suatu persamaan dikatakan lebih sederhana jika jumlah variabel
dan/atau minterm yang ada dalam persamaan itu lebih sedikit bila dibandingkan dengan
persamaan asalnya, contoh :
SISTEM DIGITAL
BAB 2 : GERBANG LOGIKA & ALJABAR BOOLE
Y(A, B, C, D) = AB’ + ABD + ABD’ + A’C’D’ + A’C’D
= A (B’ + BD + BD’) + A’ (C’D’ + C’D)
= A ((B’ + (B(D’ + D)) + A’ (C’ (D’ + D))
= A (B’+B) + A’C’
= A + A’C’
= (A+A’)(A+C’)
Y(A, B, C, D) = A+C’
22
SISTEM DIGITAL
BAB 2 : GERBANG LOGIKA & ALJABAR BOOLE
SOAL
GERBANG LOGIKA & ALJABAR BOOLE
1. Suatu rangkaian digital mempunyai persamaan Boole sbb :
F x, y   x  y ' x' y'
a. Gambarlah rangkaian digital dari persamaan di atas.
b. Sederhanakan persamaan Boole di atas dengan menggunakan Aljabar Boole.
Jawab:
a.
x
b.
y
F x, y   x  y '  x' y '
 x' y ' ( x' y ' )
 x' y ' x' y '
 x' y '
2. Sederhanakan persamaan Boole di bawah ini dengan menggunakan Aljabar Boole.
F x, y, z   x' y'' z  xy  xy'
Jawab :
F x, y, z   x' y'' z  xy  xy'
 xy  z  xy  xy'
 z  xy  xy'
 z  x( y  y ' )
zx
23
24
SISTEM DIGITAL
BAB 2 : GERBANG LOGIKA & ALJABAR BOOLE
3. Untuk rangkaian logika di bawah ini, buatlah :
A
B
C
Y1
Y
Y2
a. Persamaan Boole
b. Tabel kebenaran.
Jawab :
a. Y  A, B, C   ( A' C'( A  B' ))'
b.
A
B
C
Y1
Y1
0
0
0
1
1
0
0
1
0
1
0
1
0
1
0
0
1
1
0
0
1
0
0
0
0
1
0
1
0
0
1
1
0
0
0
1
1
1
0
0
Y
0
0
0
1
1
1
1
1