Materi tambahan File

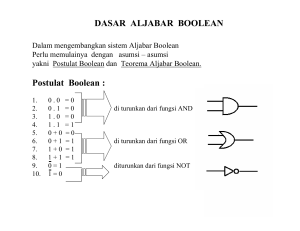
BAB IV
ALJABAR BOOLE DAN PETA KARNAUGH
4.1 Kegunaan Aljabar Boole dan Peta Karnaugh
Di dalam aplikasinya, bentuk rangkaian digital yang akan dibuat sehingga
menghasilkan sinyal yang diinginkan dari beberapa input, tidak selalu sederhana. Ada
kalanya rangkaian digital agar menghasilkan output tertentu yang diinginkan tersebut
bentuknya sangat rumit. Untuk itu diperlukan suatu upaya untuk menyederhanakan
rangkaian digital, dengan sinyal output penyederhanaan yang sama persis dengan sinyal
output sebelum rangkaian disederhanakan. Metode yang dapat digunakan adalah dengan
cara menggunakan Aljabar Boole dan Peta Karnaugh (Karnaugh Map).
4.2 Penggunaan Aljabar Boole untuk menyederhanakan Rangkaian Digital
Lain halnya dengan aljabar dalam matematika, Aljabar Boole memiliki kaidahkaidah khusus dalam menyelesaikan persamaan logika, atau dalam hal ini
menyederhanakan fungsi logika dari suatu rangkaian logika yang rumit. Kaidah-kaidah
tersebut dijelaskan dalam pembehasan berikut ini.
1. Sifat Identitas (Sifat Khusus) Aljabar Boole
(i)
A+0=A
(ii)
A+1=1
(iii)
A+A=A
(iv)
̅+A=1
A
(v)
A.0=0
(vi)
A.1=A
(vii)
A.A=A
̅.A=0
(viii) A
(ix)
̿=𝐀
𝐀
(x)
A + A.B = A
(xi)
̅ .B = A + B ............................................................................ (4.1)
A+A
19
Contoh Soal
Buktikan Sifat Identitas A + 1 = 1 dengan mnggambarkan gerbang logika dan
tabel kebenarannya.
Jawab
A
Y
1
A
1
Y = A+B
0
1
1
1
1
1
Jadi, terbukti bahwa apapun nilai input, hasilnya selalu bernilai satu, 1.
Latihan Soal
Buktikan Sifat-sifat Identitas yang lain dengan menggambarkan gerbang logika
dan tabel kebenarannya.
2. Sifat Komutatif
(i)
A+B=B+A
(ii)
A . B = B . A ................................................................................... (4.2)
3. Sifat Asosiatif
(i)
A + (B + C) = (A + B) + C
(ii)
A . (B . C) = (A . B) . C .................................................................. (4.3)
4. Sifat Distributif
(i)
A . (B + C) = A . B + A . C
(ii)
A + (B . C) = (A + B) . (A + C) ...................................................... (4.4)
5. Hukum de Morgan
(i)
̅.𝐁
̅
Y = ̅̅̅̅̅̅̅̅
A+B= 𝐀
(ii)
̅+𝐁
̅ .......................................................................... (4.5)
Y = ̅̅̅̅̅̅̅
A.B= 𝐀
20
Contoh Soal
1) Sederhanakan fungsi logika 𝑌 = 𝐴̅𝐵̅ 𝐶̅ + 𝐴̅𝐵̅ 𝐶 + 𝐴𝐵̅ 𝐶̅ + 𝐴𝐵𝐶̅ menggunakan aljabar
Boole.
JAWAB
𝑌 = 𝐴̅𝐵̅ 𝐶̅ + 𝐴̅𝐵̅ 𝐶 + 𝐴𝐵̅ 𝐶̅ + 𝐴𝐵𝐶̅
= 𝐴̅𝐵̅ (𝐶̅ + 𝐶) + 𝐴𝐶̅ (𝐵̅ + 𝐵)
(Sifat Distributif, Pers. 4.4 (i))
= 𝐴̅𝐵̅ + 𝐴𝐶̅
(Sifat Identitas, Pers. 4.1 (iv))
̅ + 𝐴̅𝐵𝐶̅ 𝐷 + 𝐴𝐵 + 𝐵𝐶𝐷 + 𝐵𝐶 menggunakan
2) Sederhanakan fungsi logika 𝑌 = 𝐵𝐶̅ 𝐷
aljabar Boole.
JAWAB
̅ + 𝐴̅𝐵𝐶̅ 𝐷 + 𝐴𝐵 + 𝐵𝐶𝐷 + 𝐵𝐶
𝑌 = 𝐵𝐶̅ 𝐷
̅ + 𝐶𝐷) + 𝐵(𝐴̅𝐶̅ 𝐷 + 𝐴 + 𝐶)
= 𝐵(𝐶̅ 𝐷
(Sifat Distributif, Pers. 4.4 (i))
̅̅̅̅̅̅̅̅
= 𝐵((𝐶
+ 𝐷 ) + ̿̿̿̿
𝐶𝐷 ) + 𝐵
Sifat Identitas, Pers. 4.1 (x)
Hukum de Morgan, Pers. 4.5 (i)
Sifat Identitas, Pers. 4.1 (ix)
̅̅̅̅̅̅̅̅
̿̿̿̿̿̿̿̿
= 𝐵((𝐶
+ 𝐷 ) + (𝐶
+ 𝐷) ) + 𝐵(𝐴̅𝐶̅ 𝐷 + 𝐴 + 𝐶)
Hukum de Morgan, Pers. 4.5 (i)
̅̅̅̅̅̅̅̅
= 𝐵((𝐶
+ 𝐷 ) + (𝐶 + 𝐷)) + 𝐵(𝐴̅𝐶̅ 𝐷 + 𝐴 + 𝐶)
Sifat Identitas, Pers. 4.1 (ix)
= 𝐵 + 𝐵(𝐴̅𝐶̅ 𝐷 + 𝐴 + 𝐶)
Sifat Identitas, Pers. 4.1 (iV)
=𝐵
(Sifat Identitas, Pers. 4.1 (xi))
21