Pertemuan 5 - Binus Repository

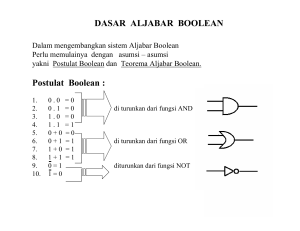
Learning Outcomes
• Mahasiswa dapat menjelaskan definisi
aljabar boole dan hukum-hukum aljabar
boole,duality dan contoh pemakaian
aljabar boole.
Outline Materi:
•
•
•
•
Definisi Aljabar Boole
Hukum-hukum Aljabar Boole
Duality
Contoh penerapan..
Pengertian
Dari teori mengenai logika proposisi dan
himpunan kita mengenal operasi-operasi
yang berlaku pada sistem tersebut, yaitu
operasi ,  pada sistem proposisi
(pernyataan) dan operasi ,  pada sistem
himpunan pada kedua sistem tersebut
berlaku beberapa sifat-sifat yang memiliki
kesamaan. Sifat-sifat pada kedua sistem
yang sama adalah sifat-sifat berikut :
Definisi Aljabar Boole
Suatu Aljabar Boole adalah sistem 5 tupel <B, +, *, ’, 0, 1> dengan arti :
B  himpunan
Boole 

  operasi binar

'  operasi unar
0  elemen zero
1  elemen unit
Elemen zero adalah identitas pada operasi +, dan elemen unit adalah identitas pada operasi . Dan
pada <B, +, *, ’, 0, 1> berlaku sifat-sifat:
Sifat-sifat Proposisi Aljabar <>Aljabar Boole
Sistem Logika Proposisi dengan
operasi , 
Sistem Himpunan dengan
operasi , 
Hukum Komutatif
Hukum Komutatif
pq  q p
A B  B  A
pq  q p
A B  B  A
Hukum Asosiatif
Hukum Asosiatif
( p  q)  r  p  (q  r )
( A  B)  C  A  ( B  C )
( p  q)  r  p  (q  r )
( A  B)  C  A  ( B  C )
Sifat-sifat Proposisi Aljabar <>Aljabar Boole (2)
Hukum Distributif
Hukum Distributif
p  (q  r )  ( p  q)  ( p  r )
A  ( B  C )  ( A  B)  ( A  C )
p  (q  r )  ( p  q)  ( p  r )
A  ( B  C )  ( A  B)  ( A  C )
Hukum Identitas
Hukum Identitas
pF  p
A  A
p T  p
AS  A
Hukum Negasi
Hukum Komplemen
p  p  T
A  A'  U
p p  F
A  A'  
Sifat-sifat Proposisi Aljabar <>Aljabar Boole(3)
Hukum De'Morgan
Hukum De'Morgan
 ( p  q)  p  q
( A  B)'  A'B'
 ( p  q)  p  q
( A  B)'  A'B'
C o n to h : x 
ja w a b : x 
y
x
 x 
 y 


x
 x  y
 y
 y


x  y
x   x   y 
 x  x    x 
0   x  y 
 x 

x

y 
 ?
Aplikasi Aljabar Boole
APLIKASI PADA RANGKAIAN GERBANG LOGIKA
(RANGKAIAN LOGIKA KOMBINASI):
1)
Input
: x, y
Output
:xy
RRangkaian seri (AND Gate)
Input
: x, y
Output
xy
:
Aplikasi Aljabar Boole(2)
Input : x, y
Output
:x
y
Input : x
Output
: x'
Aplikasi Aljabar Boole (3)
x
xy+x'y
y
TABEL KEBENARAN : Tabel kebenaran
dari suatu ekspresi bolean ditentukan
sesuai dengan nilai logika dari inputinput dan operator-operator yang dipakai
dalam suatu ekspresi boolean.
CONTOH:Tentukan
(xz)+(x'+y).
tabel
kebenaran
dari
X’+Y
(XZ)+(X’+Y)
X
Y
Z
X’
XZ
1
1
1
0
1
1
1
1
1
0
0
0
1
1
1
0
1
0
1
0
1
1
0
0
0
0
0
0
0
1
1
1
0
1
1
0
1
0
1
0
1
1
0
0
1
1
0
1
1
0
0
0
1
0
1
1
HUBUNGAN ANTARA TABEL KEBENARAN Dgn
EKSPRESI BOOLEAN
: Dari sebuah ekspresi bolean kita bisa
menetapkan tabel kebenaran ekspresi
tersebut, sebaliknya dari suatu tabel
kebenaran kita dapat menentukan suatu
ekspresi boolean yang sesuai dengan tabel
tersebut.
Penyederhanaan Rangkaian Kombinasi
Suatu rangkaian kombinasi dpt ditentukan
ekspresi bolean dari output rangkaian tsb.
Dengan hukum-hukum aljabar boole ekspresi
boolean output ini bisa disederhanakan, bila
bentuk ekspresi boolean output yang sudah
sederhana ini digambarkan rangkaian logika
kombinasinya maka rangkaian terakhir
merupakan bentuk penyederhanaan dari
rangkaian sebelumnya.
Contoh;
c
a
b
b
Contoh;
a
bb
c