PENGENALAN KOMPUTER

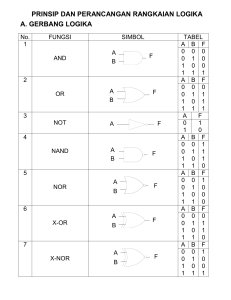
1
PENGENALAN SISTEM DIGITAL
GERBANG LOGIKA
Gerbang logika adalah piranti dua-keadaan : keluaran dengan nol volt yang
menyatakan logika 0 (atau rendah) dan keluaran dengan tegangan tetap yang
menyatakan logika 1 (atau tinggi).
Gerbang logika dapat mempunyai beberapa masukan yang masing-masing
mempunyai salah satu dari dua keadaan logika yaitu 0 dan 1. Gerbang logika dapat
digunakan untuk melakukan fungsi-fungsi khusus, misalnya AND, OR, NAND, NOR,
NOT atau EX-OR (XOR).
GERBANG AND
Gerbang AND digunakan untuk menghasilkan logika 1 jika semua masukan
mempunyai logika 1, jika tidak maka akan dihasilkan logika 0.
Simbol :
BRITISH
INTERNATIONAL
A
&
F
B
A
F
B
Tabel Kebenaran AND
MASUKAN
A
B
0
0
0
1
1
0
1
1
KELUARAN
AND
0
0
0
1
GERBANG OR
Gerbang OR digunakan untuk menghasilkan logika 1 jika salah satu masukan
mempunyai logika 1. Jika diinginkan keluaran bernilai 0, maka semua masukan
harus dalam keadaan 0.
Simbol :
BRITISH
INTERNATIONAL
A
≥1
F
A
F
B
B
Tabel Kebenaran OR
MASUKAN
A
B
0
0
0
1
1
0
1
1
KELUARAN
OR
0
1
1
1
Pengantar Informatika
2
GERBANG NOT
Gerbang NOT merupakan gerbang satu masukan yang berfungsi sebagai pembalik
(inverter). Gerbang ini menghasilkan logika 1 jika semua masukan mempunyai
logika 0, atau menghasilkan logika 0 jika semua masukan mempunyai logika 1.
Simbol :
BRITISH
INTERNATIONAL
F
A
A
F
Tabel Kebenaran NOT
MASUKAN
NOT
1
0
KELUARAN
NOT
0
1
GERBANG NAND
Gerbang NAND merupakan kependekan dari NOT-AND yang merupakan ingkaran
dari gerbang AND. Gerbang ini akan menghasilkan keluaran 0 bila semua masukan
pada keadaan 1.
Simbol :
BRITISH
INTERNATIONAL
A
&
F
B
A
F
B
Tabel Kebenaran AND
MASUKAN
A
B
0
0
0
1
1
0
1
1
KELUARAN
NAND
1
1
1
0
GERBANG NOR
Gerbang NOR merupakan kependekan dari NOT-OR yang merupakan ingkaran dari
gerbang OR. Gerbang ini akan menghasilkan keluaran 0 bila salah satu dari
masukan pada keadaan 1.
Simbol :
BRITISH
INTERNATIONAL
A
≥1
B
F
A
F
B
Pengantar Informatika
3
Tabel Kebenaran NOR
MASUKAN
A
B
0
0
0
1
1
0
1
1
KELUARAN
NOR
1
0
0
0
GERBANG XOR
Gerbang XOR (exclusive-OR) akan memberikan keluaran 1 jika masukannya
mempunyai keadaan yang berbeda. Keluaran dari gerbang ini merupakan
penjumlahan biner dari masukannya.
Simbol :
BRITISH
INTERNATIONAL
A
=1
F
A
F
B
B
Tabel Kebenaran XOR
MASUKAN
A
B
0
0
0
1
1
0
1
1
KELUARAN
XOR
0
1
1
0
UNGKAPAN BOOLE
Keluaran dari satu atau kombinasi beberapa buah gerbang dapat dinyatakan dalam
suatu ungkapan logika yang disebut ungkapan Boole. Teknik ini memanfaatkan
aljabar Boole dengan notasi-notasi khusus dan aturan-aturan yang berlaku untuk
elemen logika termasuk gerbang logika.
Aljabar Boole mempunyai notasi sebagai berikut :
1. Fungsi AND dinyatakan dengan sebuah titik (dot) sehingga sebuah gerbang AND
yang mempunyai dua masukan A dan B ditulis : F = A.B atau F = B.A
Tanda titik sering tidak ditulis sehingga persamaan di atas dapat ditulis : F = AB
atau F = BA
2. Fungsi OR dinyatakan dengan sebuah simbol plus (+) sehingga gerbang OR dua
masukan A dan B ditulis : F = A + B atau F = B + A
3. Fungsi NOT dinyatakan dengan garis atas (overline) pada masukannya sehingga
dapat dituliskan : F = Ā (dibaca NOT A atau bukan A)
4. Fungsi XOR dinyatakan dengan simbol
dan B ditulis : F = A
B
. Untuk gerbang XOR dua masukan A
Notasi NOT digunakan untuk menyajikan sembarang fungsi pembalik (ingkaran).
Sebagai contoh jika keluaran dari gerbang NAND dapat ditulis : F = A.B dan F = AB.
Ungkapan Boole untuk fungsi NOR adalah : F = A + B
Pengantar Informatika
4
GERBANG KOMBINASI
Sistem logika biasanya melibatkan lebih dari satu gerbang yang membentuk suatu
kombinasi untuk melakukan suatu fungsi tertentu.
Contoh :
A
C
F = A.B
B
Dengan menggunakan ungkapan Boole :
 Keluaran dari gerbang AND, C=A.B
 Keluaran dari gerbang NOT, F=A.B
Contoh lainnya :
Diketahui :
A
C
F
B
D
a. Tentukan ungkapan Boole-nya !
b. Buat tabel kebenaran yang menunjukkan semua keadaan sehingga dapat
dibuktikan gerbang kombinasinya dapat digantikan dengan sebuah gerbang
c. Buktikan bahwa A+B = A.B
Jawab :
a. Ungkapan Boole pada gerbang C = A, ungkapan Boole pada gerbang D = B dan
ungkapan Boole pada gerbang F= A.B
b. Tabel kebenarannya :
A
B
C
D
F
0
0
1
1
1
0
1
1
0
0
1
0
0
1
0
1
1
0
0
0
Dari tabel diatas dapat dilihat bahwa keluaran F identik dengan keluaran dari
gerbang NOR, sehingga kombinasi di atas dapat digantikan dengan gerbang NOR
c. Ungkapan Boole dari NOR adalah A+B tetapi ungkapan yang dihasilkan adalah
A.B sehingga A+B = A.B
Dari contoh di atas dapat dilihat bahwa “NOT A OR NOT B” ekivalen dengan “NOT A
AND NOT B”. Ini dikenal sebagai teorema De Morgan yang pertama. Teori yang
kedua dapat dideduksi dari untai logika :
A
C
F
B
D
A
0
0
1
1
B
0
1
0
1
C
1
1
0
0
D
1
0
1
0
F
1
1
1
0
Dari tabel dapat dilihat bahwa keluarannya sama dengan keluaran gerbang NAND,
maka dapat disimpulkan A.B = A+B
Pengantar Informatika
5
Dari teorema De Morgan di atas dapat dilihat bahwa komplemen dari sebuah fungsi
dapat diperoleh dengan membuat komplemen setiap variabel dan mengubah tanda .
menjadi tanda + dan sebaliknya, yaitu :
A+B = A.B
A.B = A+B
Beberapa teorema Boole yang lain adalah :
A.B = B.A
A+B = B+A
A.(B.C) = (A.B).C
A+(B+C) = (A+B)+C
(A+B).(A+C) = A+B.C
A.B+A.C = A.(B+C)
A+A.B = A
A.(A+B) = A
A+A.B = A+B
A.(A+B) = A.B
Contoh :
Buktikan teorema Boole A.(A+B) = A.B dengan menggunakan tabel kebenaran.
Jawab :
A
0
0
1
1
B
0
1
0
1
A
1
1
0
0
A+B
1
1
0
1
A.(A+B)
0
0
0
1
A.B
0
0
0
1
Jadi A.(A+B) = A.B
Pengantar Informatika
6
Pengantar Informatika
7
Pengantar Informatika