Hukum Pertama Termodinamika

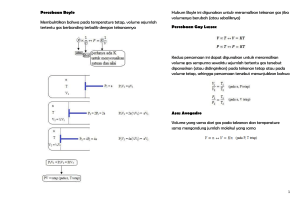
KALOR 2
Gas Ideal &
Hukum Termodinamika 1
Fenomena
• Gelembung air semakin
membesar ketika
bergerak ke atas
• Bagaimana Anda
menerangkan fenomena
ini ?
Hukum Gas
• Prinsip pemuaian tidak mampu menjelaskan ekspansi
gas
– Ketika gas memuai akan mengisi ruangan
– Volume gas juga tergantung pada tekanan
• Perlu mencari hubungan antara volume, tekanan,
temperatur dan massa  Persamaan Keadaan
• Ketika keadaan sistem berubah  akan menunggu
sampai terjadi keadaan setimbang
Balon disiram nitrogen cair
• Melembung
– ditiup (diisi oleh molekul gas, massa m)
– mempunyai volume (V)
– bentuknya tetap: Pi = Po
• Disiram Nitrogen cair
– temperaturnya (T) diturunkan
Hukum gas ideal
• Robert Boyle (1627-1691)
– Pada temperatur konstan 
P >> bila V << dan
sebaliknya
– P berbanding terbalik dgn V
 PV = konstan
– Berlaku pada hampir semua
gas dengan kerapatan
rendah
• Jacques Charles (1746-1823)
Gay Lussac (1778-1850)
– Pada kerapatan rendah, untuk
gas
• Temperatur absolut sebanding
dengan tekanan pada volume
konstan
• Temperatur absolut sebanding
dengan volume pada tekanan
konstan
PV = CT
– C sebanding dengan jumlah
gas sehingga
PV = NkT
• N = jumlah molekul gas
• k = konstanta Boltzman 1,381 x
10-23 J/K
Terkadang lebih mudah
menyatakan jumlah gas
dalam mol daripada dalam
molekul sehingga
PV = nRT
• N = n NA
– NA = bilangan avogadro 6,022 x
1023 molekul/mol
– n = jumlah mol gas
• R = konstanta gas umum
= 8,314 J/mol.K
= 0,08206 L.atm/mol.K
• Gas ideal didefinisikan sebagai gas dimana PV/nT
konstan untuk seluruh tekanan.
• Persamaan keadaan gas ideal
PV = nRT
• Massa molar M, massa 1 mol unsur/senyawa
– Massa molar 12C = 12 g/mol
• Massa n mol gas m = nM
• Kerapatan gas ideal
– Pada temperatur tertentu,
kerapatan gas ideal sebanding
dengan tekanan
m
nM

V
V
M
 
P
RT
 
• Perilaku gas ideal  perilaku gas nyata pada kerapatan
dan tekanan rendah
• Untuk sejumlah gas tertentu PV/T = konstan, sehingga
dapat ditulis
P1 V1 P2 V2

T1
T2
Interpretasi molekuler tentang temperatur:
teori kinetik gas
•
•
Temperatur gas adalah ukuran energi kinetik rata2 molekul2 gas
Asumsi-asumsi
– Gas terdiri dari sejumlah molekul yang bertumbukan elastik satu sama
lain dan dgn dinding wadah
– Molekul terpisah secara rata2 oleh jarak yang besar dibandingkan dgn
diameter masing2 dan tidak saling memberikan gaya kecuali bila
bertumbukan  gas ideal
– Tanpa adanya gaya eksternal, tidak ada posisi yang dicenderungi oleh
molekul dalam wadah dan tidak ada kecenderungan arah vektor
kecepatan
• Energi kinetik rata2 (translasi) untuk gerak
satu arah (sb x saja)
K x ,ratarata  12 kT
• Energi kinetik translasi molekul rata2
(temperatur menjadi ukuran)
K ratarata  32 kT
• Energi kinetik translasi total n mol gas
mengandung N molekul
K  NKratarata  32 NkT  32 nRT
• Kelajuan rata2
vrms 
3kT

m
3RT
M
Hukum Pertama Termodinamika
• Pernyataan kekekalan energi
• Percobaan Joule
– Dibutuhkan 4,18 satuan usaha mekanik untuk menaikkan
temperatur 1 g air 1oC
– 4,18 J = 1 kal energi panas  ekivalensi mekanis dari panas
– Cara lain pakai generator listrik, melepas air jatuh dari
ketinggian tertentu
– Usaha yang dilakukan harus menjadi pertambahan energi
internal sistem (perubahan temperatur/perubahan fasa)
contoh
• Bila sebuah tabung air yang terisolasi secara
termis dijatuhkan dari ketinggian h dan
membentur tanah secara tak elastis, berapa h
agar temperatur air naik 1 oC?
Agar temperatur naik 1 oC maka energi internal air
harus naik 4,18 J utk tiap gram air.
mgh = m (4,18kJ/kg)
h = 426 m
Hukum Pertama Termodinamika
• Panas neto yang ditambahkan pada
suatu sistem sama dengan
perubahan energi internal sistem
ditambah usaha yang dilakukan oleh
sistem.
Q = ΔU + W
Q = +  panas masuk ke sistem
-  panas keluar dari sistem
U = energi internal sistem
W = +  usaha dilakukan oleh sistem
-  usaha dilakukan pada sistem
contoh
• Sebuah pemanas air menggunakan listrik sebagai
sumbernya digunakan untuk memanaskan 3 kg air pada
80oC. Usaha yang diberikan filamen pemanas 25 kJ
sementara panas yang terbuang karena konduksi
sebesar 15 kkal. Berapa perubahan energi internal
sistem dan temperatur akhir ?
Panas terbuang 15 kkal = 62,7 kJ
Q = ΔU + W
-62,7 kJ = ΔU -25 kJ  ΔU = -37,7 kJ
 37,7kJ
o
T 


3
,
01
C
o
4,18kJ / kg Cx3kg
T’ = 76,9oC
• U  sifat sistem, tergantung keadaan sistem
• Sistem (P1 V1) diperlakukan  P2 V2 U2 T2 jika
dikembalikan ke kondisi awal maka P1 V1 serta
T1 dan U1
• Q dan W bukan fungsi keadaan sistem.
• Untuk jumlah besaran Q, U dan W yang sangat
kecil dQ = dU + dW
Energi internal gas ideal
• Temperatur gas ideal dihubungkan dengan
energi kinetik translasi molekul2 gas
K = 3/2 nRT
• Jika energi translasi ini diambil sbg energi
internal total gas, maka U hanya tergantung
pada temperatur tidak pada volume atau
tekanan
U = 3/2 nRT
• Jika ada energi lain maka pers U akan berharga
lain dr pers di atas, misal ada gaya tarik menarik
antar molekul.
Percobaan Joule
• Apakah energi internal tergantung volume?
• A = gas, B = kosong, sistem terisolasi termis dan tidak ada usaha
yang bekerja oleh dan pada sistem.
• Kran dibuka, gas dr A menerobos ke B  ekspansi bebas, lalu gas
mencapai kesetimbangan
• Uawal = Uakhir  temperatur konstan
• Volume bertambah energi potensial krn gaya tarik naik  energi
kinetik translasi turun  temperatur turun
• Eksperimen Joule  temperatur konstan, hanya berlaku utk gas
ideal (kerapatan rendah)
• Energi internal hanya tergantung pada temperatur
Usaha dan diagram PV untuk gas
• Usaha mesin2  mengubah energi termis menjadi
usaha yg dapat dipakai
• Gas berekspansi  menggerakkan piston
– Mesin uap, uap panas menggerakkan piston
– Mesin bensin, uap bensin + udara meledak, ekspansi yang cepat
• Piston digerakkan perlahan, maka gas akan
mengembang/merapat tanpa pernah jauh dari keadaan
kesetimbangan  proses kuasi-statik
• Tidak ada percepatan pada gerak piston, ada gaya
eksternal PA yang mendorong melawan piston, maka
kerja yang dilakukan gas pada piston
dW = F dx = PA dx = P dV
– Kompresi  dV negatif, usaha dilakukan pada gas
– Ekspansi  dV positif, usaha dilakukan oleh gas
• Usaha  diagram PV
Luas A
F = PA
gas
F
dx
• Usaha = luas daerah di bawah kurva
(Po, Vo)
W   P dV
P
ΔV
• Ekspansi isobarik
• 1 L.atm = 101,3 J
• Persamaan gas ideal PV = nRT
V
contoh
• Gas ideal P1V1 = P2V2 = nRT (temperatur akhir sama)
• Lintasan A, gas dipanaskan, volume membesar V2 lalu didinginkan,
tekanan menurun P2. Usaha P1(V2 – V1)
• Lintasan B, gas didinginkan, tekanan turun P2 lalu dipanaskan dgn
tekanan konstan, volume membesar V2. Usaha P2(V2-V1)
• Lintasan C, tekanan dan volume berubah sepanjang proses,
temperatur konstan  ekspansi isotermis
V2
Wisotermis  nRT ln
V1
P (P1, V1)
P
(P2, V2)
V
Lintasan A
P
(P1, V1)
Lintasan B
(P1, V1)
(P2, V2)
(P2, V2)
V
V
Lintasan C
Proses siklis
• Usaha yang dilakukan dan panas yang diberikan
hanyalah tergantung pada bagaimana sebuah sistem
berubah dari satu keadaan ke keadaan lain, tetapi
perubahan energi internal tidak bersifat demikian
• WAB = P(VB – VA) = 2 L.atm
• WCD = P(VD-VC) = -1 L.atm
• Usaha neto = WAB – WCD = 1 L.atm
• Jika energi internal konstan maka harus ditambahkan
panas sebesar 1 L.atm
P (atm)
A
B
2
1
D
C
1
2
V (L)
Proses Isotermal
• Selama proses temperatur sistem tetap
konstan
A
B
Proses Isotermal
• Misalkan suatu gas ideal berada pada kontainer
dengan piston yang bebas bergerak
– Saat awal keadaan sistem (gas) pada titik A
– Ketika Q diberikan pada sistem  terjadi ekspansi ke
B
– Temperatur (T) dan massa gas (m) konstan selama
proses
U  32 n R T  0
Hk. Termodinamika ke-1: U = Q – W = 0
W=Q
Proses Adiabatik
• Selama proses tidak terjadi transfer panas yang
masuk atau keluar sistem
Proses adiabatik terjadi pada sistem terisolasi atau dapat
terjadi pada sistem yang mempunyai proses yang sangat cepat
Q=0
Hk. ke-1: U = Q – W = 0
U = - W
Proses Adiabatik
• Perbedaan Diagram PV untuk gas Ideal antara
proses adiabtik ( 1 – 2 ) dan isotermal
Contoh Proses adiabatik
Piston motor
Proses Isobarik
• Selama proses tidak terjadi perubahan tekanan pada
sistem
Pada umumnya terjadi pada sistem yang mempunyai kontak langsung
dengan tekanan atmosfer bumi yang dianggap konstan (misal: reaksi
biokimia)
Proses Isokhorik
• Selama proses volume sistem tidak mengalami perubahan
• Disebut juga proses: volume konstan, isometrik, isovolumik
Proses ini terjadi pada sistem yang mempunyai volume (wadah) yang
kuat, tertutup dan tidak dapat berubah
V = 0 , jadi W = 0
Hk. ke-1: U = Q – W = 0
U = Q
• SR-71 Blackbird dengan panjang 107 feet 5 inch adalah salah satu
pesawat tercepat di dunia. Pada ketinggian 80.000 feet kecepatannya
dapat mencapai mach 3. Ketika mendarat setelah penerbangan yang
jauh pesawat ini sekitar 30 menit sangat panas untuk disentuh dan
ternyata panjangnya bertambah 6 inch dibanding ketika take off. Jika
koefisien muai linier blackbird 24 x 10-6 K-1 dan suhu ketika take off
23oC, berapa suhu blackbird ketika baru saja mendarat?
• What mass of steam initially at 130°C is needed to warm 200 g of
water in a 100-g glass container from 20.0°C to 50.0°C? What if the
final state of the system is water at 100°C? Would we need more or
less steam?
• Suppose 1.00 g of water vaporizes isobarically at atmospheric
pressure (1.013 x 105 Pa). Its volume in the liquid state is Vi = Vliquid
= 1.00 cm3, and its volume in the vapor state is Vf = Vvapor = 1 671
cm3. Find the work done in the expansion and the change in internal
energy of the system. Ignore any mixing of the steam and the
surrounding air—imagine that the steam simply pushes the
surrounding air out of the way.
• Sebuah pemanas listrik memiliki daya 3 kW digunakan untuk
mendidihkan 1,5 kg air dengan suhu 18oC. Berapakah energi yang
diperlukan untuk menaikkan suhu air hingga titik didihnya? Berapa
waktu yang diperlukan untuk mencapai titik didih air?
kuis
Mesin 4 langkah