Uploaded by
common.user76243
Gas Sifat Hukum Gas kirim

Model Gas Ideal
1.
2.
3.
4.
1
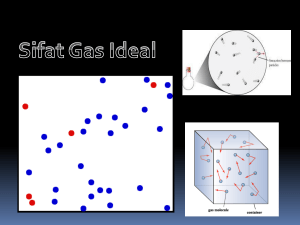
Terdiri atas partikel (atom atau molekul)
yang jumlahnya besar
Partikel-partikel tersebut tersebar merata
dalam seluruh ruang
Partikel-partikel tersebut bergerak acak
ke segala arah
Jarak antar partikel jauh lebih besar dari
ukuran partikel
Model Gas Ideal
1.
2.
3.
2
Tidak ada gaya interaksi antar partikel
kecuali bila bertumbukan
Semua tumbukan (antar partikel atau
dengan dinding) bersifat lenting
sempurna dan terjadi dalam waktu
yang sangat singkat
Hukum Newton tentang gerak berlaku
3
Gas ideal adalah gas teoretis yang
terdiri dari partikel-partikel titik yang
bergerak secara acak dan tidak saling
berinteraksi.
Konsep gas ideal sangat berguna
karena memenuhi hukum gas ideal,
sebuah persamaan keadaan yang
disederhanakan, sehingga dapat
dianalisis dengan mekanika statistika.
Gas ideal - Wikipedia bahasa Indonesia, ensiklopedia bebas
https://id.wikipedia.org/wiki/Gas_ideal
Tekanan gas
4
1
standard atmosphere = 1 atm =
tekanan udara pada suhu 0 0C,
ketinggian setara permukaan laut, =
tinggi kolom air raksa (mercury/Hg) 760
mm.
1
mm Hg ketinggian air raksa = 1/760
atm = 1 torr (menghormati Evangelista
Torricelli, 1643)
1
atm (tepatnya 0,99 atm) = 105 Pascal
0,99
atm = 1 bar (dari: barometer)
GAS IDEAL
5
Pada kondisi normal seperti temperatur
dan tekanan standar, kebanyakan gas
nyata berperilaku seperti gas ideal.
Banyak gas seperti nitrogen, oksigen,
hidrogen, gas mulia dan karbon
dioksida dapat diperlakukan seperti gas
ideal dengan perbedaan yang masih
dapat ditolerir.
SIFAT-SIFAT GAS IDEAL
6
Hukum Gas Ideal
Sifat fisik gas dikontrol oleh tiga variabel
berikut:
1. Tekanan yang digunakan oleh gas.
2. Volume yang ditempati oleh gas.
3. Temperatur gas.
A. Hukum Gas Ideal
7
1. Hukum Boyle
jika gas dalam ruang tertutup suhu
mutlak dijaga konstan maka
volume gas berbanding terbalik
dengan tekanannya.
P1V1 = P2V2
PV = konstan
Gas dalam tabung tertutup
2. Hukum Charles
8
V
konstan
T
V1
V2
T1 T2
Keterangan:
V1 = volume awal
(m3)
V2 = volume akhir
(m3)
T1 = suhu awal (K)
T2 = suhu akhir (K)
Jacques Charles (1747–1823) dan
disebut dengan hukum Charles, yang
menyatakan bahwa
jika gas dalam ruang tertutup
tekanannya dijaga konstan maka
volume gas dalam jumlah tertentu
berbanding lurus dengan temperatur
mutlaknya.
3. Hukum Gay-Lussac
Jika gas dalam ruang tertutup volume
dibuat konstan maka tekanan gas
berbanding lurus dengan temperatur
mutlaknya.
P
konstan
T
P1
P2
T1 T2
9
Persamaan Boyle-Gay-Lussac.
PV
konstan
T
10
…….(*)
PV
P2V2
1 1
T1
T2
Keterangan:
V1 dan V2 = volume gas pada keadaan 1 dan 2 (m3)
P1 dan P2 = tekanan gas pada keadaan 1 dan 2 (N/m2)
T1 dan T2 = suhu mutlak gas pada keadaan 1 dan 2 (K)
Orang memberikan sejumlah gas pada balon,
11
yang berakibat volume balon mengembang. Di
sini terjadi penambahan jumlah partikel gas atau
sejumlah massa gas ke dalam balon. Oleh karena
itu, jumlah pertikel perlu diperhitungkan, sehingga
konstanta di sebelah kanan pada persamaan (*)
dikalikan dengan banyaknya partikel N, yang
selanjutnya ditulis menjadi:
PV
Nk
T
PV NkT
Keterangan:
P = tekanan gas (N/m2) N = banyak partikel
V = volume gas (m3) T = suhu mutlak (K)
Konstanta k adalah konstanta Boltzmann dalam sistem
SI besarnya: k = 1,381 × 10–23 J/K
12
●
Satu mol sebuah zat adalah banyaknya
zat yang mengandung atom-atom atau
molekul-molekul sebanyak bilangan
Avogadro.
● Bilangan Avogadro ditulis dengan NA
yang didefinisikan sebagai banyaknya
atom karbon dalam 12 gram 12C.
NA = 6,022 1023 atom/mol
●
Jika banyak mol gas adalah n maka dapat
13
ditulis:
N
n
NA
PV nRT
R = 8,314 103 J/kmol K
Keterangan:
P = tekanan gas (N/m2)
V = volume gas (m3)
n = mol gas (kmol)
R = tetapan gas umum (8.314 J/kmol K)
T = suhu mutlak (K)
Massa n mol gas ditulis:
m n Mr
atau
14
m
n
Mr
Massa jenis gas ideal ()
M
P
RT
Keterangan:
m = massa gas
Mr = massa molekul relatif
Hukum Dalton (1803)
P total
P
15
= P1 + P2 + P3 + dst
= Pressure = tekanan gas
Berlaku
konstan
pada Volume (V) dan suhu (T)
Hukum Graham
16
Thomas Graham (1846):
Aliran gas melalui saluran kecil (pori-pori)
disebut “effusion”.
kecepatan effusi berbagai gas tidak
sama.
Kecepatan effusi gas berbanding
terbalik dengan kuadrat dari massa jenis
gas
Kecepatan effusi gas berbanding
terbalik dengan kuadrat dari massa
molar gas
Hukum Graham
Pada
suhu (T) dan tekanan (P)
yang sama, dua macam gas
memiliki energi kinetik (Ek) yang
sama:
Ek1
½
= Ek2
m1 v12 = ½ m2 v22
v12
/ v22 = m2 / m1
(v1 /
v2)2= (m2 / m1)
(v1 /
v2) = (m2 / m1)
17
Hukum Graham
(v1 /
v2) = (m2 / m1)
Laju
effusi1 / Laju effusi2 =
(massa jenis2 / massa jenis1) =
Laju
effusi1 / Laju effusi2 =
(massa molar2 / massa molar1)
bisa
juga
Laju
effusi1 / Laju effusi2 =
massa molar2 / massa molar1)
18
PERSAMAAN VAN DER WALLS UNTUK
GAS NYATA
a
P + ------V2
(V – b) = RT
an2
P + ------ (V – nb) = nRT
V2
19
a/V2 adalah
internal pressure
menunjukkan
atraksi antar
molekul.
B adalah
excluded volume
menunjukkan
voleme gas yang
sudah tidak bisa
ditekan
Contoh
Seorang
20
pasien paru-paru didukung
pernafasan buatan dalam bentuk
aliran gas Oksigen (O2) dan Helium
(He). Pada kondisi STP (Standard
Temperature and Pressure) massa jenis
O2 adalah 1,43 g/L, sedang He 0,179
g/L. Mana gas yang lebih cepat laju
effusinya?
Laju
effusi He / Laju effusi O2 =
(O2 /He) =
{(1,43 g/L)/(0,179g/L)} = 2,83
jadi:
Laju
effusi He lebih cepat 2,83 kali
dibanding Laju effusi O2
21
B. Tekanan Gas Ideal Menurut
Kinetik
Teori
22
Gas ideal dibuat anggapan-anggapan sebagai
berikut.
a. Gas terdiri dari banyak partikel.
b. Partikel-partikel gas senantiasa bergerak
dengan kecepatan dan arah yang beraneka
ragam.
c. Partikel gas tersebar secara merata di semua
bagian ruang yang ditempati.
d. Jarak antarpartikel gas jauh lebih besar
daripada ukuran partikelnya. Diameter partikel
2,5×10–10 m, sedangkan jarak antarpartikel
3 × 10–19 m.
23
e. Gaya atau interaksi antarpartikel sangat
kecil sehingga diabaikan.
f. Terjadi tumbukan antara partikel dengan
dinding, dalam tumbukan tersebut
dianggap tumbukan lenting sempurna.
g. Dinding tempat gas itu licin sempurna.
h. Hukum-hukum Newton tentang gerak
berlaku.
Besarnya tekanan gas dalam kubus ialah:
24
F
P
A
N
Px
N
Py
Keterangan:
P = tekanan (N/m2)
F = gaya (N)
A = luas penampang (m2)
m vx2
V
m vy 2
V
N m vz2
Pz
V
Diagram gerakan partikel gas
dalam dinding bejana
vx
2
1 2
v
3
vx2 vy2 vz2
Persamaan tekanan gas pada ruang tertutup
25
dirumuskan:
1 (Nmv2 )
P
3
V
2N
P
Ek
3V
3
Ek = kT
2
Keterangan:
P = tekanan gas (N/m2)
N = jumlah partikel
v = kecepatan rata-rata (m/s)
m = massa partikel (kg)
V = volume gas (m3)
Ek = energi kinetik
Persamaan di atas adalah energi kinetik sebuah
partikel gas, sedangkan energi kinetik sistem
dengan N buah partikel adalah
3
Ek = NkT
2
Keterangan:
Ek = energi kinetik rata-rata sistem (J)
N = jumlah partikel
k = konstanta Boltzmann (J/K)= 1,38 × 10–23 J/K
T = suhu mutlak (K)
26
vrms
3RT
=
M
vrms
3P
=
3kT
m
Keterangan:
27
vrms = akar kuadrat kecepatan rata-rata (m/s).
M = massa tiap satuan mol (kg)
m = massa tiap satuan partikel (kg)
P = tekanan gas (N/m2)
ρ = massa jenis gas (kg/m3)
C. Teorema Ekuipartisi Energi
1
Ek 3 kT
2
Angka 3 pada persamaan energi tersebut
menunjukkan tingkat kebebasan molekul
menyerap energi.
Untuk gerak translasi ada 3 kebebasan
dalam menyerap energi, yaitu kebebasan
bergerak ke
arah sumbu x, sumbu y, dan
sumbu z.
1
1
1
2
2
Ek mvx mvy mvz2
2
2
2
28
Pada gas diatomik tingkat kebebasan molekul
29
dapat menyerap energi, selain memiliki 3 tingkat
kebebasan gerak translasi juga masih memiliki 2
tingkat kebebasan berotasi yaitu kebebasan
berotasi dalam dua arah yang berbeda. Sehingga
molekul gas diatomik memiliki 5 derajat kebebasan
menyerap energi, maka besar energinya adalah:
1
Ek 5 kT
2
Teorema semacam ini
dinamakan ekuipartisi
energi.
Jika tingkat kebebasan dinyatakan dengan f
maka rata-rata energi kinetik per molekul ditulis:
1
Ek f kT
2
U = N Ek
Keterangan:
U = energi dalam gas (J)
Ek = energi kinetik rata-rata tiap molekul gas (J)
N = banyak partikel
30
Energi Dalam Gas Ideal
Adalah jumlah energi (energi kinetik translasi, rotasi, vibrasi serta
energi potensial elastik) yg dimiliki oleh seluruh molekul gas
dalam wadah tertentu.
f = derajat kebebasan
1. Gas Monoatomik (f=3), seperti He, Ne, Ar
U 32 NkT
2. Gas Diatomik, seperti O2, N2, H2
Pada suhu rendah (T = ± 250 K), f=3
U 32 NkT
Pada suhu sedang (T = ± 500 K), f=5
Pada suhu tinggi (T = 7± 1000 K), f=7
U 52 NkT
U 2 NkT
U NE Nf ( 12 kT )
Contoh 1
Suatu tabung punya volume 10 L,
mengandung gas yang tekanannya 760 torr.
Kemudian tabung diperlonggar hingga
tekanannya mengecil menjadi 700 torr.
Berapa volume gas sekarang?
V1 = 10 L
P1 = 760 torr
P2 = 700 torr
V2 = .........?
V1x P1 = V2 x P2
10 L x 760 torr = V2 x 700 torr
V2 = (10 L x 760 torr) / 700 torr = 10,9 torr
32
Contoh 2
33
Suatu tabung punya volume 580 mL,
mengandung gas yang tekanannya 0,2 atm.
Kemudian gas dimampatkan hingga
volumenya menjadi 100 mL. Berapa tekanan
gas sekarang?
P1 = 0,2 atm
V1 = 580 mL
V2 = 100 mL
P2 = .........?
P1 x V1 = P2 x V2
0,2 atm x 580 mL = P2 x 100 mL
P2 = (0,2 atm x 580 mL) /100 mL = 1,16 atm
Contoh 3
Suatu
34
gas volumenya 10 mL, suhunya
20 0C. Kemudian suhu didinginkan
menjadi 0 0C. Berapa volumenya
sekarang?
V1
= 10 mL
T1
= 20 0C = (20 + 273) K = 293 K
T2
= 0 0C = (0 + 273) K = 273 K
V2
= ........?
Jawab Contoh 3
V2
V1
T1
=
T2
10 mL
293 K
V2
=
35
V2
=
273 K
10 mL x 273 K
293 K
= 9,32 mL
Contoh 4
36
Satu gram Radium melepaskan
partikel alpha berupa ion He2+ dengan
laju 1,16 x 1018 partikel / tahun. Tiaptiap partikel tersebut menjadi gas
Helium:
He2+ + 2 e- He
Pada kondisi standar, tiap 1,16 x 1018
molekul He memiliki volume 0,043 mL
Berapa banyak molekul dalam 1 Liter
He?
Jawab Contoh 4
37
N1 = 1,16 x 1018 molekul He
V1 = 0,043 mL
V2 = 1 L = 1000 mL
N2 ..............?
N2 / V2 = N1 / V1
N2 / 1000 mL = 1,16 x 1018 molekul He / 0,043 mL
N2 = (1,16 x 1018 molekul He / 0,043 mL) x 1000 mL
N2 = 2,7 x 1022 molekul He
N1
V1
N2
=
V2
38
20 % O2 dan 80 % N2
Berarti P N2 = Ptot . (0,8)/(0,2+0,8) = 0,8 atm
PV = nRT
0,8 atm. V = (7 gram/28 gr/mol). (0,082
L.atm/mol.K ).(300 K)
V = ……..Liter.
39
Pada T derajad Kelvin, kecepatan gas = V1
Pada 2T derajad Kelvin, kecepatan gas = V2
Bagaimana besarnya V2 terhadap V1.