LAT MATRIKS

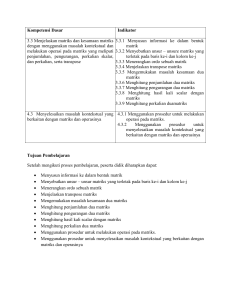
−6 2𝑝
2 1
2 −1 0 1
1. Nilai p yang memenuhi persamaan matriks 2 (
)+(
)=(
)(
) adalah . . .
−1 3
1 1
2 4
4 −1
3 2
, B=
0 5 
2. Diketahui matrik A = 
 x  1
 y 1  dan C =


 0  1
 15 5  , A’ adalah transpos dari A.


Jika A’ . B = C maka nilai 2x + y = ….
𝑥+𝑦
𝑥
3. Diketahui matriks 𝐵 = (
) dan
−1
𝑥−𝑦
𝑥
1
−2
𝐶=(
). Jika matriks A merupakan transpos matriks B dan A = C, maka nilai dari 𝑥 − 2𝑥𝑦 +
−2𝑦 3
𝑦 sama dengan . . . .
𝑎
4. Diketahuipersamaanmatriks A = BT (BTadalah transpose matriks B), dengan A = (
2𝑏
2𝑐 − 3𝑏 2𝑎 + 1
B=(
). Nilai a + b + c = …
𝑎
𝑏+7
a b   2 3


 
3
4
c
d

=


5. Diketahui persamaan matriks
  1 2  2  4

 

 3 4 1 2 
Maka a + b + c + d = ….
6. Diketahui persamaan matriks :
𝑎 4
2
(
)+(
−1 𝑐
𝑑
1 −3 0 1
𝑏
)=(
)(
)
3 4
0 1
−3
Nilai a+b+c+d = .......
7.
 
a
c
b
d
3
2
 
4
2 ==
4
2

2
0 . Nilai a – 2b + c = ….
 2  3  x   8 
8. Jika 
     , maka 4𝑥 + 5𝑦 = . . . .
 3 1  y   1 
4
)dan
3𝑐
3 
2
9. Diketahui matriks A  
dan
  1  2 


12 
 6
B =
. Jika A2 = xA + yB, maka nilai xy = ….
  4  10 


2 - 1 
 dan B =
3 4
10.Jika diketahui matriks A = 
1 2
2
- 2 1 , maka A .B = …


11.(Soal UN Tahun 2013)
Diketahui matriks 𝐴 = (
x + 2xy + y adalah…
−3 −1
3 𝑦
𝑥 5
8
) . Jika A + B – C= (
), 𝐵 = (
) dan 𝐶 = (
𝑦
9
−3 6
−𝑥
5 −1
5𝑥
), maka
−4