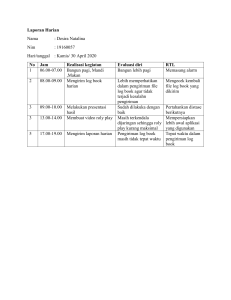
1
2
3
4
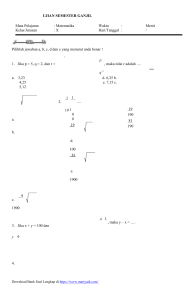
Bentuk akar dari 𝑎 × 𝑎 × 𝑎 × 𝑎 adalah..
A
𝑎+4
B
4𝑎
C
𝑎4
D
4×𝑎
E
6𝑎7
Bentuk sederhana dari 3𝑎2 × 2𝑎4 adalah. . .
A
5𝑎6
B
6𝑎8
C
6𝑎6
D
5𝑎8
E
6𝑎7
Bentuk sederhana dari (𝑝2 )5 × (𝑝2 )3 adalah…
A
𝑝12
B
𝑝16
C
𝑝15
D
𝑝35
E
𝑝60
Bentuk sederhana dari
A
𝑎6
B
𝑎5
C
𝑎−1
D
𝑎−5
𝑎 4 𝑎 −2
𝑎 −3
adalah. . .
E
5
6
3
Bentuk 125𝑎3 sama dengan. . .
A
25𝑎3
B
25𝑎
C
5𝑎
D
5𝑎9
E
5𝑎3
Bentk sederhana dari 4𝑎2 𝑏4 × 2𝑎3 𝑏6 adalah. . .
A
6𝑎5 6𝑏10
B
6𝑎 6𝑏24
C
8𝑎5 𝑏10
D
8𝑎5 𝑏24
E
7
8
𝑎−11
8𝑎6 𝑏24
Bentuk sederhana dari
A
𝑎𝑏
B
𝑎𝑏−5
C
𝑎8 𝑏−6
D
𝑎15 𝑏 −5
E
𝑎15 𝑏 −3
𝑎 3 𝑏 2 ×𝑎 5 𝑏 −4
𝑎 7 𝑏 −3
Hasil dari 32 × 37 adalah. . .
A
32
B
35
C
37
adalah. . .
9
D
39
E
314
Nilai dari 3log 729 adalah…
A
B
C
D
E
5
6
7
8
9
2
2
2
10 Jika log 12 = 3,6 dan log 3 = 1,6 maka nilai dari log 36 adalah. . .
A
B
C
D
E
11
2
log 16 + 2log 4 – 2log 2 = . . .
A
B
C
D
E
12
6
7
3
4
5
1
2
log 16 + 2log 4 = …
A
B
C
D
E
13
4,2
4,6
5,2
5,6
6,2
1
2
3
4
5
3
log 1 + 3log 3 + 3log 9 + 3log 27 =
A
B
C
D
E
3
4
5
6
7
1
14 Nilai logaritma dari 3log 81
adalah . . .
A
B
C
D
E
5
-4
4
-5
3
a
b
a
15 Jika diketahui log 3 = log 27 maka nilai dari log b adalah. . .
A
B
C
D
E
6
-5
-3
4
3
3
16 Nilai dari log (18 x 9) adalah . . .
A
B
C
D
E
4
5
6
7
8
x
17 Nilai x jika log 125 = 3 adalah. . .
A
B
C
D
E
3
4
5
6
7
18 Hasil dari 3 6 + 24 =. . .
A
4 6
B
5 6
C
6 6
D
7 6
E
8 6
19
4 3 + 5 3 − 8 3 =. . .
A
4 3
B
9 3
C
3
D
−3 3
E
17 3
20
5( 3 + 11) =
A
15
B
15 + 55
C
5 14
D
5 + 55
E
55
21
berapakah panjang AC dari bangun datar di atas adalah..
A 5
B 6
5
C
D
6
E
13
22 Bentuk sederhana dari 4−5 3 adalah . . .
A
20 − 5 3
13
5
B
13
C
5
D
5
7
7
(4 − 3)
(4 + 3)
(4 − 3)
5
E
4− 3
23 Bentuk sederhana dari
A
2( 30 + 40)
B
−( 30 + 40)
C
30 + 40
D
30 − 40
E
− 30 + 40
24
2× 3=⋯
A
23
B
6
C
2 3
D 6
5
E
25
14
2
=⋯
2 5
6− 8
adalah. . .
A
1
14
2
B 7
7
C
26
D
28
E
12
Jika 𝑥 = 2 maka nilai x yang memenuhi adalah. . .
A
B
C
D
E
1 atau 2 saja
-1 atau 2
-2 atau 2
-2
2
27 Himpunan penyelesaian dari 2𝑥 + 3 = 9 adalah. . .
A
B
C
D
E
-6,3
-3,3
-3,6
2,3
-3,2
28 Nilai x yang memenuhi persamaan 2𝑥 − 6 = −2 adalah . . .
A
B
C
D
E
2
2 atau 4
-2 atau 4
4
Tidak ada yang memenuhi
29 Himpunan penyelesaian dari 2𝑥 + 2 = 4𝑥 − 8 adalah
A
B
C
D
E
{1,5}
{1}
{5}
{-1,5}
{-1.-5}
30 Jika 2𝑥 + 1 = 𝑥 − 2 maka nilai x yang memenuhi adalah
A
B
1 atau 3
1
3
atau -3
C − 13 atau -3
D 2 atau 3
E -2 atau -3
31 Nilai x yang menuhi 3𝑥 − 6 − 𝑥 + 2 = 0 adalah
A
B
C
D
E
2 atau 3
1 atau 4
2 atau 4
1 atau 3
1 atau 2
32 Nilai x yang memenuhi persamaan 𝑥 + 1 + 𝑥 − 3 = 8 adalah. . .
A
B
C
D
E
-3 atau 5
2 atau 5
-3 atau 0
3 atau 5
Tidak ada yang memenuhi
33 Himpunan penyelesaian dari 2𝑥 + 1 = 3 adalah . . .
A
B
C
D
E
{-2,0}
{-2,1}
{0,2}
{1,2}
{1}
34 Nilai x yang memenuhi pertidaksamaan 𝑥 − 2 < 3 adalah…
A
𝑥 < −1
B
𝑥>5
C
−1 < 𝑥 < 0
D
−1 < 𝑥 < 5
E
0<𝑥<5
35 Himpunan penyelesaian dari pertidaksamaan 3 − 𝑥 > 2 adalah. .
A
𝑥>1
B
𝑥<5
C
1<𝑥<5
D 𝑥 < 1 atau 𝑥 > 5
E
36
−1 < 𝑥 < 5
Himpunan penyelesaian dari pertidaksamaan 4𝑥 − 3 ≤ 1 adalah. . .
1
A
𝑥≥2
B
𝑥≤1
C
1
D
𝑥≥1
2
≤𝑥≤1
E 𝑥 ≤ 12 atau 𝑥 ≥ 1
37 Interval nilai x yang memenuhi 3𝑥 − 6 ≤ 18 adalah. .
A 𝑥 ≤ −8 atau 𝑥 ≥ 4
B
−8 ≤ 𝑥 ≤ 4
C
𝑥 ≤ −4 atau 𝑥 ≥ 8
D
−4 ≤ 𝑥 ≤ 8
E
4≤𝑥≤8
38 Hasil dari 15 − −6 + −1 =. . .
A
B
C
D
E
5
6
7
9
10
39 Nilai 2 + 𝑥 − 𝑥 2 untuk x = -5 adalah. . .
A
B
C
D
E
1
3
5
9
13
40 Diketahui 𝑓 𝑥 = 2𝑥 − 1 dan 𝑔 𝑥 = 5 − 𝑥 . Nilai f(3)-g(3) adalah.. .
A
B
C
D
E
1
2
3
5
7