momentum, impuls, hukum kekekalan momentum dan

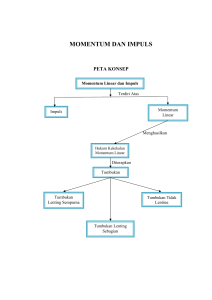
MOMENTUM, IMPULS, HUKUM KEKEKALAN
MOMENTUM DAN TUMBUKAN
Oleh:
Edi susanto
5202415018
01
Pendidikan teknik otomotif S1
definisi
Momentum suatu benda yang bergerak
didefinisikan sebagai hasil perkalian antara
massa dengan kecepatan benda
 Momentum merupakan sebagai ukuran
kesungkaran sesuatu benda di gerakan
maupun di berhentikan

:
rumus
Secara matematis dirumuskan:
P=m.v
Keterangan :
●p
: momentum (kg m/s)
●m
: massa benda (kg)
●v
: kecepatan benda (m/s)
Contoh soal
1. Sebuah benda bermassa 1 ton, bergerak dengan kecepatan 90
km/jam. Berapa momentum yang dimiliki benda tersebut?
Jawab:
Diketahui: m = 1 ton → 1000 kg
V = 90 km/jam → 25 m/s
P = ......?
P = m .v
= 1000 . 25
= 25.000 Ns
definisi

Impuls adalah peristiwa gaya yang bekerja pada benda
dalam waktu hanya sesaat

Impuls didefinisikan sebagai hasil kali gaya dengan waktu
yang dibutuhkan gaya tersebut bekerja

Contoh aplikasi:
bola ditendang,
bola tenis dipukul
karena pada saat tendangan dan pukulan, gaya yang bekerja
sangat singkat.
rumus

Dari definisi tersebut dapat dirumuskan seperti berikut:
I = F .
∆t

Keterangan:

●I
: Impuls (Ns)

●F
: Gaya (N)

● ∆t
: Waktu (s)
Impuls dapat dihitung juga dengan cara menghitung luas kurva dari grafik F vs waktu t.
Contoh soal
Sebuah bola ditendang dengan gaya sebesar 48N dalam waktu 0,8 sekon.
Berapakah besar impuls pada saat kaki menyentuh bola.
Jawab:
Diketahui:
F = 48N
∆t = 0,8 s
I = ......?
I
= F . ∆t
= 48 x 0,8
= 38,4 Ns
IMPULS SAMA DENGAN PERUBAHAN MOMENTUM
Menurut hukum ke-2 Newton
F=m.a
Dengan subsitusi kedua persamaan tersebut maka diperoleh :
Keterangan:
●m
: massa (kg)
I = F . ∆t = m.v2 – m.v1
● V1
: kecepatan awal (m/s)
● V2
: kecepatan akhir (m/s)
CONTOH SOAL
Sebuah benda diam yang memiliki massa 500 g, setelah mendapat
gaya,
kecepatannya 25 m/s. Berapa besar impuls tersebut?
Jawab:
Diketahui: m = 500 g → 0,5 kg
V2 = 25 m/s
V1 = 0 m/s
I
= m . V2 - m . V1
= 0,5 . 25 – 0,5 . 0
= 12,5 Ns
HUBUNGAN MOMENTUM DAN IMPULS

mudah untuk mengukur impuls yaitu dengan bantuan momentum.
Berdasarkan hukum Newton II, apabila suatu benda dikenai suatu gaya, benda
akan dipercepat.
Keterangan:
a=
𝐅
𝐦
● a = percepatan (m/s2)
● F = gaya (N)
● m = massa benda (kg)
Sehingga terdapat hubungan antara impuls dan momentum:
F
V−Vo
=
Δt
m
Keterangan :
F . Δt = m (V – Vo)
I
= Impuls
∆p = Perubahan Momentum
I = m . V – m .V2
I = p – po
I = Δp
Penjumlahan momentum mengikuti aturan penjumlahan vektor, secara
matematis:
p = p1 + p 2
Jika dua vektor momentum p1 dan p2
CONTOH SOAL
Dalam sebuah permainan sepak bola, seorang pemain melakukan
tendangan pinalti. Tepat setelah ditendang bola melambung dengan
kecepatan 60 m/s. Bila gaya bendanya 300 N dan sepatu pemain
menyentuh bola selama 0,3 s maka tentukan:
Impuls yang bekerja pada bola
Perubahan momentumya,
Massa bola
Jawab:
V0 = 60 m/s
F = 300 N
∆t = 0,3 s
Impuls yang bekerja pada bola sebesar:
I
= F . ∆t
= 300 . 0,3
= 90 Ns
Perubahan momentum bola sama dengan besarnya impuls
yang diterima:
∆p = 90 kg m/s
Massa bola dapat ditentukan dengan hubungan berikut:
∆p
=I
m . ∆v
= 90
m . (60-0)= 90
90
60
m
=
m
= 1,5 kg
HUKUM KEKEKALAN MOMENTUM
“jika tidak ada gaya luar yang bekerja pada sistem, maka momentum total
sesaat sebelum sama dengan momentum total sesudah tumbukan”
Penurunan rumus secara umum dapat dilakukan dengan meninjau gaya interaksi saat terjadi
tumbukan berdasarkan hukum Newton III.
Faksi = – Freaksi
F1 = – F2
Impuls yang terjadi selama interval waktu Δt adalah F1 Δt = -F2 Δt . kita ketahui bahwa I = F Δt =
Δp, maka persamaannya menjadi seperti berikut:
Δp1 = – Δp2
m1v1 – m1v’1 = -(m2v2 – m2v’2)
m1v1 + m2v2 = m1v’1 + m2v’2
p1 + p2 = p’1 + p’2
Jumlah Momentum Awal = Jumlah Momentum Akhir
Keterangan:
p1,p2
p‘1, p’2
m1, m2
v1, v2
v’1, v’2
= momentum benda 1 dan 2 sebelum tumbukan
= momentum benda 1 dan 2 sesudah makanan
= massa benda 1 dan 2
= kecepatan benda 1 dan 2 sebelum tumbukan
= kecepatan benda 1 dan 2 sesudah tumbukan
Contoh aplikasi
Saat peluru ditembakkan ke kanan dengan alat jarak jauh seperti remote,
senapan akan tertolak ke kiri. Percepatan yang diterima oleh pistol ini berasal
dari gaya reaksi peluru pada pistol (hukum Newton III).
Mula-mula sistem roket diam, sehingga momentumnya nol. Sesudah gas
menyembur keluar dari ekor roket, momentum sistem tetap. Artinya momentum
sebelum dan sesudah gas keluar sama
CONTOH SOAL

1. Sebuah peluru dengan massa 50 g dan kecepatan 1.400 m/s mengenai dan
menembus sebuah balok dengan massa 250 kg yang diam di bidang datar tanpa
gesekan. Jika kecepatan peluru setelah menembus balok 400 m/s, maka hitunglah
kecepatan balok setelah tertembus peluru!

Jawab:

Diketahui: m1 = 50 g = 0,05 kg

V1
= 1.400 m/s

V2
=0

V’1 = 400 m/s

V’2 = ......?

m1 . v 1 + m2 . v 2
=

0,05 . 1.400 + 250 . 0

70
m1 . v’1 + m2 . v’2
=
=
20 + 250 v’2

v’2
=
(70 - 20) : 250

v’2
=
0,2 m/s
0,05 . 400 + 250 . v’2

2. Bola A bermassa 600 g dalam keadaan diam, ditumbuk oleh bola B bermassa 400 g yang
bergerak dengan laju 10 m/s. Setelah tumbukan, kelajuan bola B menjadi 5 m/s, searah
dengan arah bola semula.

Tentukan kelajuan bola A sesaat setelah ditumbuk bola B!

Jawab:

Diketehui: m1
= 600 g = 0,6 kg

m2
= 400 g = 0,4 kg

v1
=0

v2
= 10 m/s

v’2
= 5 m/s

v’1
= .....?

m1 . v1 + m2 . v2 =
m1 . v’1 + m2 . v’2

0,6 . 0 + 0,4 . 10 =
0,6 . v’1 + 0,4 . 5

0+4
=
0,6 v’1 + 2
4-2
=
0,6 v’1
=
0,6 v’1

2

2 / 0,6


= v’1
3,3 = v’1
Jadi kelajuan benda A setelah tumbukan adalah 3,3 m/s
TUMBUKAN
Tumbukan sentral adalah tumbukan yang terjadi bila titik pusat
benda yang satu menuju ke titik pusat benda yang lain.
LENTING
SEMPURNA
TUMBUKAN
TIDAK
LENTING
SAMA
SEKALI
LENTING
SEBAGIAN
TUMBUKAN LENTING SEMPURNA
Pada lenting sempurna berlaku hukum kekekalan energi dan hukum kekekalan
momentum
Kekekalan
Momentum
Nilai
koefisien
elastisitas
TUMBUKAN
LENTING
SEMPURNA
Kecepatan
sebelum dan
sesudah
tumbukan
Kekekalan
energi
kinetik
1. Kekekalan Momentum
Keterangan:
m1
= massa benda 1 (kg)
m2
= massa benda 2 (kg)
v1
= kecepatan awal benda 1 (m/s)
v2
= kecepatan awal benda 2 (m/s)
v’1
= kecepatan akhir benda 1 (m/s)
v’2
= kecepatan akhir benda 2 (m/s)
2. Kekekalan energi kinetik
Ek1 + Ek2 = Ek’1 + Ek’2
1/2 m1 v12 + 1//2 m2 v22 = 1/2 m1 (v’1)2 + 1/2 m2 (v’2)2
3. Kecepatan sebelum dan sesudah tumbukan
-(v’1 – v’2) = v1 – v2
4. Nilai koefisien elastisitas / koefisien restitusi (e) pada tumbukan lenting sempurna berlaku:
TUMBUKAN LENTING SEBAGIAN
koefisien restitusi pada kejadian ini berkisar antara nol sampai satu (0< e < 1).
keterangan: h’= tinggi pantulan benda
h = tinggi benda semula / tinggi pantulan sebelumnya
TUMBUKAN TIDAK LENTING SAMA SEKALI
“terjadi apabila dua benda setelah tumbukan menjadi satu dan bergerak
bersama-sama”
Pada tumbukan ini terjadi pengurangan enrgi kinetik sehingga energi kinetik total
benda-benda setelah terjadi tumbukan akan lebih kecil dari energi kinetik total
benda sebelum. Dengan demikian:
Contoh soal
1. Sebuah mobil mainan bermassa 1 kg mula-mula bergerak ke kanan dengan kelajuan 10 m/s. Mobil mainan tersebut menabrak
mobil kedua yang bermassa 1,5 kg yang bergerak dengan kecepatan 5 m/s.
Berapakah kecepatan mobil mainan ini setelah tumbukan jika tumbukan dianggap tumbukan lenting sempurna?

Contoh

Jawab:

Diketahui: m1 = 1 kg m2 = 1,5 kg

v1 = 10 m/s v2 = 5 m/s

v1’= ....? v2’= ......?

e= −(v1′−v2′)v1−v2

1=−(v1′−v2′)10−5

5=-v1’+v2’.......(i)

5 = -v1’+v2’

17,5 = v1’ + 1,5 v2’ +

22,5 = 0 + 2,5 . v2’

22,5 = 2,5 . v2’

22,52,5 = v2’
v1’ = 9 - 5

9 m/s = v2’
v1’ = 4 m/s
m1.v1 + m2.v2 = m1.v1’ + m2.v2’
1.10 + 1,5.5 = 1. v1’ + 1,5.v2’ 1=(v1′+v2′)5 10 + 7,5 = v1’ + 1,5 v2’
17,5 = v1’ + 1,5 v2’...(ii)
5 = -v1’+v2’
5 = -v1’+ 9
2. Balok kayu tergantung oleh seutas tali yang panjangnya I=40 cm. Balok
tersebut ditembak mendatar dengan sebutir peluru yang bermassa 20 gr dan
kecepatan vp. Massa balok 9,98 kg dan percepatan gravitasi 10 m/s. Jika peluru
mengenai balok bersarang di dalamnya sehingga balok dapat bergerak naik
setinggi 10 cm maka:
Berapakah kecepatan peluru tersebut?

Jawab:

Diketahui:
mp = 20 gr = 0,02 kg

mb = 9,98 kg

g
= 10 m/s

h
= 10 cm = 0,1 m

vp
=......?

Pada ayunan balistik tersebut dapat dibagi menjadi dua bagian yaitu
tumbukan dan gerak AB. Pada gerak AB berlaku hukum kekekalan energi
sehingga dapt diperoleh vb’ seperti:

Eka

1/2mvb2 =

vb2
= 2 . 10 . 0,1

vb2
= √2

Tumbukan peluru dan balok. Pada tumbukan ini berlaku kekekalan energi.

pawal =
pakhir

mp . vp
= (mp + mb) vb’

0,02.vp
= (0,02 + 9,98) . √2

vp
=

vp
= 500 √2 m/s
=
Epb
mgh
10√2
0,02
m/s
3.Sebuah bola tenis dilepas dari ketinggian 200 m. Jatuh mengenai lantai hingga
elastis sebagian.
Hitunglah tinggi pemantulan pertama yang dapat oleh bola tenis! (e=0,2)
Jawab:
Diketahui:

e
h1
= 0,2
h2

= 200 m
= .....?
h2

e
=√h1

0,2
=√200

0,04 =

h2

Jadi, tinggi bola setelah memantul adalah 8 m.
h2
h2
200
= 0,04 x 200 = 8 m