Descriptive Statistic - E

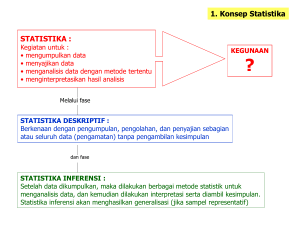
Descriptive Statistic
Asal- Usul kata
• “Status” (bahasa Yunani yang berarti “State” =
Negara)
• Istilah ini mula-mula diartikan sebagai
kumpulan data tentang negara, termasuk
catatan mengenai penduduk, pemilikan tanah,
angka kelahiran, kematian, dsb.
Definisi
 Statistics is the science of data. This involves
collecting, classifying, summarizing, organizing,
analyzing, and interpreting numerical information
(McClave and Sincich, 2003).
 Statistics is the science of designing studies,
gathering data, and then classifying,
summarizing, interpreting, and presenting these
data to explain and support the decisions that are
reached (Sanders and Smidt, 2000).
DISTRIBUSI FREKUENSI
a. Menentukan jumlah kelas
K = 1 + 3,3 Log N
b. Menentukan interval kelas
Ci = Range / K
c. Menentukan Lower class limit dan Upper
Class Limit
yaitu batas atas dan batas bawah dari
suatu kelas
d. Mid Point
MP = (Lower Limit + Uper limit)/2
Menentukan jumlah kelas

Menentukan jumlah kelas
K = 1 + 3,3 Log N
 K = jumlah kelas
N = banyaknya frekuensi
3.3 = bilangan konstan
Menyusun data dalam bentuk Array
41
57
65
70
75
87
45
57
65
71
75
89
49 51 52 53 55 56 56
58 59 59 60 61 61 62 63 63
65 67 67 67 67 69 69 69 69
71 71 73 73 73 73 73
77 77 77 77 79 81 83 83
89 91 91 91 92 93 94 96
a. Menentukan jumlah kelas
K = 1 + 3,3 Log N
K = 1 + 3,3 Log 60
K = 1 + 3,3 (1,78)
K = 6,8 atau 7
b. Menentukan Interval Kelas
Range
K
96  41
Ci 
6,8
Ci 
= 8,09 dibulatikan 9
Histogram dan Poligon
20
18
16
14
12
10
8
6
4
2
0
20
18
16
14
12
10
8
6
4
2
0
1
2
3
4
5
6
7
1
2
3
4
5
6
7
Arithmatic Mean (Rata-rata Hitung)
• Metode Panjang
fX

X
N
f
n
X
A
Ci
d
Metode Pendek
fd

X  A
xCi
N
= frekuensi
= jumlah data
= nilai data
= Assumed mean
= interval kelas
= deviasi dalam interval
Arithmatic Mean (Rata-rata Hitung)
 Rata-rata hitung sederhana (Simple Arithmatic Mean)
X
X


N
 Contoh Data tidak Berkelompok
Data berikut adalah besarnya uang saku yang dikirim oleh
10 orang tua mahasiswa dari luar Yogya ( dalam ribuan
rupiah ) adalah sebagai berikut :
 300
450 350 600
575 250
625 650
650 550
Rata-rata Hitung Terbobot (Weighted Mean)
• Tiap kasus atau frekuensi dikalikan dengan
bobot, kemudian dibagi dengan jumlah bobot.
XW

X 
W
Weighted Mean
• Secara subyektif
Pemberian faktor penimbang didasarkan pada pandangan masing-masing
individu
• Secara obyektif
Penentuan faktor penimbang ditentukan berdasarkan arti penting barang
Rumus
X 
 XW
W
Jenis
Barang
Harga per Kg
( X)
Beras
Gula
Garam
Rp. 5.000
Rp. 3.750
Rp. 900
Weight
Subyektif
5
3
2
∑ Ws = 10
Weight
Obyektif
50 kg
5,0 kg
0,5 kg
∑ Wo = 55,5
Contoh Kasus
Kelas
30
40
50
60
70
80
90
-
39
49
59
69
79
89
99
F
Nilai Tengah
(x)
Fx
d
fd
4
6
8
12
9
7
4
34,5
44,5
54,5
64,5
74,5
84,5
94,5
138
267
436
774
670
591
378
-3
-2
-1
0
1
2
3
-12
-12
-8
0
+9
+14
+12
50
fd

X  A
xCi
N
3.225
3
X  64,5 
x10
50
3
Median
• Median suatu rangkaian data adalah nilai
tengah dari rangkaian data yang telah disusun
secara berurut.
• Data tak Berkelompok
• Data Bercacah Ganjil
•2
3
4
• Cari letak median
N 1
2
5
5
Median
• Data tak berkelompok
• Data Bercacah Genap
• 2 3
4
5
5
N 1
2
6
Contoh Median
Distribusi
30
40
50
60
70
80
90
601
-
39
49
59
69
79
89
99
F
Tepi Kelas
4
6
8
12
9
7
4
50
Letak median = N/2
= 50/2
= 25
601
F Kum
29.5
0
39.5
4
49.5
10
59.5
18
69.5
30
79.5
39
89.5
46
99.5
50
1
Md=25
Modus atau Mode
 Modus dari suatu rangkaian data adalah nilai data yang paling
sering muncul (frekuensi terbesar) dalam rangkaian data itu.
 a. Data:
2
3
4
5
6
Karena data ini masing-masing frekuensi (kemunculan)-nya hanya 1,
maka dikatakan tidak memiliki modus.
 b. Data: 2
3
4
4
5
6
Frekuensi terbesar ada 1 (nilai empat muncul dua kali). Jadi modusnya
adalah 4. Rangkaian data yang memiliki satu modus disebut Monomodus.
 c. Data: 2
3
4
4
5
6
6
7
Frekuensi terbesar ada dua (muncul dua kali) yaitu angka 4 dan 6. Jadi
modus rangkaian data ini adalah 4 dan 6. Rangkaian data ini memiliki 2
Modus atau disebut Bi-modus.