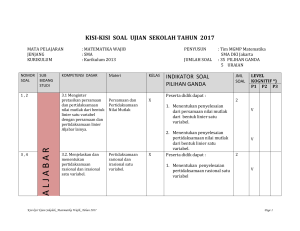
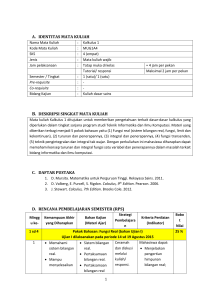
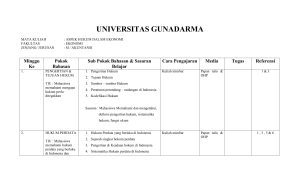
silabus matematika sma
advertisement

SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran : Matematika Satuan Pendidikan : SMA / MA Kelas/Semester : X/1 Nama Guru NIP/NIK Sekolah : ........................... : ........................... : ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : X / UMUM Semester : GANJIL Sandar Kompetensi: 1. Memecahkan masalah yang berkaitan dengan bentuk pangkat, akar, dan logaritma Kompetensi Dasar Materi Ajar 1.1. Menggunakan Bentuk Pangkat, aturan pangkat, Akar, dan akar, dan Logaritma. logaritma. - Sifat - sifat bila-ngan berpangkat dengan pangkat bulat positif, pangkat bulat negatif, dan nol. Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Kegiatan Pembelajaran - Memberikan contoh bentuk perkalian berulang. Indikator Pencapaian Kompetensi - Menyederhanakan bentuk suatu bilangan berpangkat. Penilaian Teknik Tugas individu. Bentuk Instrumen Uraian singkat. Alokasi Waktu Contoh Instrumen 1. Sederhanakanlah. a. x7 : x2 b. - Menyimak pemahaman dan pendeskripsian tentang bilangan berpangkat, bilangan pokok (basis), dan pangkat (eksponen). - Menyimpulkan atau mendefinisikan sifat- sifat bilangan berpangkat 5 x 2 y 4 4 x5 y 22 x 2 y 2 (menit) 2 × 45 menit Sumber /Bahan/ Alat Sumber: Buku paket (Buku Matematika SMA dan MA ESIS Kelas X Semester Ganjil Jilid 1A, karangan Sri Kurnianingsi h, dkk) hal. 1-6, 7-9, dan 10-13. Buku referensi lain. Alat: dengan pangkat bulat positif, negatif, dan nol. - Laptop - LCD - OHP - Menentukan hasil operasi aljabar pada bentuk pangkat dengan mengaplikasikan rumus - rumus bentuk pangkat. - Menyederhanakan bentuk bilangan berpangkat. - Mengubah bentuk pangkat negatif dari suatu bilangan ke bentuk pangkat positif, dan sebaliknya. - Mengenal dan memahami pengertian notasi ilmiah. - Menyatakan suatu bilangan yang sangat besar atau sangat kecil ke dalam notasi ilmiah. - Menyatakan notasi ilmiah ke dalam suatu a. p q p 3 2 - Menyatakan bilangan yang berpangkat bulat negatif ke dalam bentuk bilangan yang berpangkat bulat positif, dan sebaliknya. - Notasi Ilmiah. 2. Nyatakan bilangan berikut dalam pangkat positif dan sederhanakan. - Mengubah suatu bilangan ke bentuk notasi ilmiah, dan sebaliknya. q 3 p q 3 p q 2 3 b. 5 1 2 1 2 2 3 3. Nyatakan bilangan berikut dalam notasi ilmiah. a. 0,0000002578 b. 820.000.000.000.0 00 bilangan. - Menghitung dan menyatakan hasil operasi bilangan (perkalian dan pembagian) ke dalam notasi ilmiah. - Bilangan rasional. - Bilangan irrasional (bilangan bentuk akar). - Menjelaskan definisi dan contoh bilangan rasional. - Memeriksa apakah suatu bilangan termasuk bilangan rasional atau bukan. - Menuliskan bilangan bilangan rasional di antara dua buah bilangan. - Menjelaskan definisi dan contoh bilangan irrasional (bilangan bentuk akar). - Menunjukkan bahwa suatu bilangan merupakan bilangan irrasional (bilangan bentuk - Mengidentifikasi apakah suatu bilangan termasuk bilangan rasional atau bilangan irrasional (bilangan bentuk akar). Tugas individu. Uraian singkat. - Di antara bilanganbilangan berikut, manakah yang merupakan bilangan bentuk akar? a. 7 d. 9 e. 12 f. 49 b. 38 c. 2 × 45 menit Sumber: Buku paket hal. 14, 15-16, 17. Buku referensi lain. Alat: - Laptop 3 36 - LCD - OHP akar). - Menyederhanakan bilangan bentuk akar. - Operasi aljabar pada bentuk akar. - Menentukan hasil operasi aljabar (penjumlahan, pengurangan, perkalian, pembagian) pada bentuk akar dengan mengaplikasikan rumus - rumus bentuk akar. - Melakukan operasi aljabar pada bentuk akar. Tugas kelompok. Uraian singkat. - Nyatakan penjumlahan dan pengurangan berikut dalam bentuk akar yang sederhana. 2 × 45 menit Sumber: Buku paket hal. 18-22. Buku referensi lain. a. 2 3 4 3 b. 4 6 24 54 Alat: - Laptop - LCD - - OHP Menyederhanaka n bentuk akar a b 2 ab a b 2 ab dan Merasionalka n penyebut pecahan bentuk akar. - Menentukan sekawan suatu bilangan. - Merasionalkan penyebut pecahan bentuk akar dengan mengalikan pembilang dan penyebut pecahan dengan sekawan - Merasionalkan penyebut pecahan yang berbentuk akar. Tugas individu. Uraian singkat. - Rasionalkan penyebut tiap pecahan berikut. a. d. 18 3 3 2 × 45 menit Sumber: Buku paket hal. 23-28. Buku referensi lain. 2 3 5 Alat: - Laptop dari penyebut. b. - Bilangan berbentuk n a atau 1 a n untuk 1 a n dan n himpunan bilangan asli. - Mengubah pangkat pecahan negatif menjadi pangkat pecahan positif. - Persamaan pangkat sederhana dengan bilangan pokok sama. - Menyimpulkan atau mendefinisikan bilangan dalam bentuk akar dan bilangan bentuk pangkat pecahan. - Mengubah bentuk akar ke bentuk pangkat, dan sebaliknya. - Menggunakan sifat bilangan dengan pangkat rasional untuk menyelesaikan persoalan. Kuis Uraian singkat. - OHP 3 2 2 2 2 c. Pangkat rasional: - LCD 5 e. - 2 3 5 3 7 1. Nyatakan bilangan - bilangan berikut dalam bentuk pangkat. 2 × 45 menit Sumber: a. 8 Buku paket hal. 28-31, 32-33, 3336. d. 1 5 Buku referensi lain. b. 2 32 Alat: e. 53 1 27 - Laptop - - Menyatakan suatu bilangan dengan pangkat rasional ke dalam bentuk akar. - Mengubah pangkat pecahan negatif menjadi pangkat pecahan positif. - Mengubah pangkat pecahan negatif menjadi pangkat pecahan positif. - Menyelesaikan persamaan pangkat sederhana (persamaan eksponen) dengan bilangan pokok yang sama. - Menyelesaikan persamaan pangkat sederhana (persamaan c. 3 5 2. Sederhanakanlah bentuk a4 2 4b LCD - OHP 12 3. Tentukan nilai x dari persamaan 2x1 16 2 eksponen) dengan bilangan pokok yang sama. - Sifat-sifat bilangan berpangkat dengan pangkat bulat positif, pangkat bulat negatif, dan nol. - Notasi Ilmiah. - Bilangan rasional. - Bilangan irrasional (bilangan bentuk akar). . Operasi aljabar pada bentuk akar. Merasionalka n penyebut pecahan bentuk akar. - Pangkat rasional. - Melakukan ulangan berisi materi yang berkaitan dengan bilangan berpangkat (pangkat bulat positif, negatif, dan nol), notasi Ilmiah, bilangan rasional, irrasional, atau bilangan bentuk akar, operasi aljabar pada bentuk akar, merasionalkan penyebut pecahan bentuk akar, serta pangkat rasional. - Mengerjakan soal dengan baik berkaitan dengan materi menge-nai bilangan berpang-kat (pangkat bulat positif, negatif, dan nol), notasi Ilmiah, bilangan rasional, irrasional, atau bilangan bentuk akar, operasi aljabar pada bentuk akar, merasionalkan penyebut pecahan bentuk akar, serta pangkat rasional. 1. Ulan gan haria n. Pilihan ganda. Uraian singkat. a 1 2a 1 a. a2 a2 d. a a2 b. a a2 e. a2 2a c. a2 a2 ... 2. Sederhanakan bentuk akar berikut ini. a. 125 d. 4 16 b. 4 81 e. 4 81 c. 3 27 2 × 45 menit - - Pengertian logaritma. Sifat-sifat logaritma (operasi aljabar logaritma). - Menyimpulkan atau mendefinisikan logaritma dan sifat - sifat logaritma. - Mengubah bentuk pangkat ke bentuk logaritma, dan sebaliknya. Tugas kelompok. Uraian singkat. - Mengubah bentuk logaritma ke dalam bentuk pangkat, dan sebaliknya. - Menentukan hasil operasi aljabar pada bentuk logaritma dengan mengaplikasikan rumus - rumus bentuk logaritma. 1. Ubahlah ke dalam bentuk logaritma. a. 1 62 x b. 23 c. 256 4 x 2 × 45 menit Sumber: Buku paket hal. 36-38, 38-43. Buku referensi lain. 1 8 1 2. 3 - Melakukan operasi aljabar pada bentuk logaritma. Alat: Sederhanakanlah log 1 3 log 54. 2 - Laptop - LCD - OHP - - Penentuan logaritma dan antilogaritm a dengan tabel - Menentukan logaritma suatu bilangan dengan menggunakan tabel logaritma atau kalkulator. atau kalkulator. - Logaritma untuk perhitungan. - Menentukan antilogaritma suatu bilangan dengan menggunakan tabel antilogaritma atau kalkulator. - Menentukan Tugas logaritma dan individu. antilogaritma dari suatu bilangan dengan tabel yang bersesuaian (tabel logaritma atau tabel antilogaritma) atau kalkulator, serta menggunakan logaritma untuk perhitungan. Uraian singkat. Tentukan nilai dari logaritma berikut. a. log 45,458 b. log 144,3 c. log 0,05 d. log 0,098 e. log 0,001 2 × 45 menit Sumber: Buku paket hal. 44-47, 48-50, 5152. Buku referensi lain. Alat: - Laptop - LCD - OHP - Menggunakan logaritma untuk perhitungan. - - Pengertian logaritma. - Melakukan ulangan berisi materi yang berkaitan dengan pengertian logaritma, sifatsifat logaritma, serta cara menentukan logaritma dan antilogaritma dengan tabel atau kalkulator. Sifat-sifat logaritma (operasi aljabar logaritma). - Penentuan logaritma dan antilogaritm a dengan tabel atau kalkulator - Mengerjakan soal dengan baik berkaitan dengan materi mengenai pengertian dan sifat - sifat logaritma, serta cara menentukan logaritma dan antilogaritma dengan tabel atau kalkulator. Ulangan harian. Pilihan ganda. Sifat-sifat bilangan dengan pangkat b. 2,5 e. 0,6 c. 2 Uraian singkat. Rasa ingin tahu Mandiri Berorientasi tugas dan hasil Percaya diri Menyederhanakan bentuk aljabar yang memuat - Menyederhanakan bentuk aljabar yang memuat bentuk pangkat, log 2 2 log8 3 log9 2 ×245 menit log12 adalah……. d. 1,5 perhitungan. - Nilai a. 5 - Logaritma untuk 1.2. Melakukan manipu-lasi aljabar dalam perhitu-ngan 1. Tugas individu. Uraian singkat. 2. Jika 5 log 6 a , maka 36 log125 =… a. 2 3a d. 1 2a b. 3 2a e. 1 2a c. 1 3a Bentuk sederhana dari 2 × 45 menit Sumber: Buku paket hal. 5-9, 17-28, dan yang melibatkan pangkat, akar, dan logaritma. bulat. - Bentuk akar. Kreatif Kerja keras Keorisinilan pangkat bulat. akar, dan logaritma. 38-43. 1 a4 2 adalah .... 4b2 - Menyederhanakan bilangan bentuk akar. Buku referensi lain. Alat: - Sifat-sifat logaritma. - Menyederhanakan bentuk aljabar yang memuat logaritma. - Laptop - LCD - OHP - Menggunakan konsep bentuk pangkat, akar, dan logaritma untuk menyelesaikan soal. - Sifat-sifat bilangan berpangkat bulat positif. - Sifat-sifat logaritma. - Melakukan pembuktian tentang sifat-sifat sederhana pada bentuk pangkat, akar, dan logaritma. - Membuktikan sifat- sifat sederhana tentang bentuk pangkat, akar, dan logaritma. Tugas kelompok. Uraian obyektif. Buktikan bahwa 2 × 45 menit x a a a log log x log y y , a 0 , a 1, dan x, y 0 Sumber: Buku paket hal. 4-6, dan 38-43. Buku referensi lain. Alat: - Laptop - LCD - OHP - Sifat bilangan dengan pangkat - Melakukan ulangan berisi materi yang berkaitan dengan - Mengerjakan soal dengan baik berkaitan dengan materi Ulangan harian Pilihan ganda. 1. Jika 2 × 45 menit rasional. Merasionalk an penyebut pecahan bentuk akar. - Sifat-sifat dari logaritma serta bilangan berpangkat bulat positif. sifat dari bilangan berpangkat rasional dan berpangkat bulat positif, merasional kan penyebut pecahan bentuk akar, dan sifat-sifat dari logaritma. mengenai sifat dari bilangan berpangkat rasional dan berpangkat bulat positif, merasionalkan penyebut pecahan bentuk akar, dan sifatsifat dari logaritma. 2 3 x3 y 4 F x0 dengan x 64 dan y 16 , maka nilai F =..... a. 16 d. 16 27 b. 8 e. 16 81 c. 2 Uraian obyektif. 2. Dengan cara merasionalkan bagian penyebut 12 18 6 ekuivalen dengan….. ....………………………………… Mengetahui, Guru Mata Pelajaran Matematika Kepala Sekolah __________________ __________________ NIP/NIK. NIP/NIK. SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : X / UMUM Semester : GANJIL Sandar Kompetensi : 2. Memecahkan masalah yang berkaitan dengan fungsi, persamaan dan fungsi kuadrat serta pertidaksamaan kuadrat. Penilaian Kompetensi Dasar Materi Ajar Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran Indikator Pencapaian Kompetensi Teknik 2.1. Memahami - Fungsi, konsep fungsi. Persamaan Kuadrat, dan Pertidaksamaa n Kuadrat. - Pengertian fungsi. Rasa ingin tahu Berorientasi tugas dan hasil - Mendeskripsikan pengertian fungsi. Percaya diri Keorisinilan - Memahami konsep tentang relasi antara dua himpunan melalui contohcontoh. Mandiri Kreatif Kerja keras - Mengidentifikasi ciri-ciri relasi yang merupakan fungsi. - Menjelaskan peristiwa seharihari yang dapat dipandang sebagai fungsi. - Menentukan - Membedakan relasi yang merupakan fungsi dan yang bukan fungsi. Tugas individu . Bentuk Instrumen Uraian singkat. Contoh Instrumen 1. Perhatikan diagram berikut. (a) (b) Diagram manakah yang mendefinisikan Alokasi Waktu Sumber / Bahan / (menit) Alat 2 × 45 menit Sumber: Buku paket (Buku Matematik a SMA dan MA ESIS Kelas X Semester Ganjil Jilid 1A, karangan Sri Kurnianing sih,dkk) hal. 63-65, 65-69. Buku referensi lain. daerah asal (domain) dan daerah kawan (kodomain), serta daerah hasil (range) dari fungsi. - Grafik fungsi aljabar sederhana dan fungsi kuadrat. Alat: - Laptop 2. Berikan sebuah contoh dari masing masing jenis fungsi. - LCD - OHP - Mengidentifikasi jenis-jenis dan sifat fungsi. - Fungsi aljabar sederhana dan kuadrat. 2.2. Menggambar grafik fungsi aljabar sederhana dan fungsi kuadrat. fungsi? Jelaskan. - Mendeskripsikan karakteristik fungsi berdasarkan jenisnya, yaitu karakteristik dari beberapa fungsi aljabar sederhana (fungsi konstan, fungsi identitas, fungsi modulus (nilai mutlak), fungsi linear) dan fungsi kuadrat. Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan - Menentukan nilai fungsi dari fungsi aljabar sederhana (fungsi konstan, fungsi identitas, fungsi modulus, fungsi linear), dan fungsi kuadrat. - Membuat tafsiran geometris dari hubungan antara nilai variabel dan nilai fungsi pada fungsi aljabar sederhana dan fungsi kuadrat yang bersesuaian. - Mengidentifikasi fungsi aljabar sederhana dan fungsi kuadrat. - Menggambar grafik fungsi aljabar sederhana (fungsi konstan, fungsi identitas, fungsi modulus, fungsi linear), dan fungsi kuadrat. Tugas individu . Uraian singkat. - Gambarkan grafik fungsi kuadrat dengan persamaan sebagai berikut. a. y x2 2 x 3 b. y 3x2 8x 7 2 × 45 menit Sumber: Buku paket hal. 65-69, 9799. Buku referensi lain. c. y 2x2 x 5 Alat: - Laptop - LCD - OHP - Menggambar grafik fungsi aljabar sederhana dan grafik fungsi kuadrat menggunakan hubungan antara nilai variabel dan nilai fungsi pada fungsi aljabar sederhana dan fungsi kuadrat yang bersesuaian. - Menentukan sumbu simetri dan titik puncak grafik fungsi kuadrat dari grafiknya. - Merumuskan hubungan antara sumbu simetri dan titik puncak grafik fungsi kuadrat dan koefisien koefisien fungsi kuadrat. - Menentukan sumbu simetri dan titik puncak grafik fungsi kuadrat dari rumus fungsinya. - Menggambar grafik fungsi kuadrat menggunakan hasil analisis rumus fungsinya. - Mengidentifikasi definit positif dan definit negatif suatu fungsi kuadrat dari grafiknya. 2.3. Menggunakan - Persamaan sifat dan kuadrat dan aturan tentang penyelesaianpersamaan nya. dan pertidaksamaa n kuadrat. Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan - Mendeskripsikan bentuk umum dan contoh dari persamaan kuadrat. - Mencari akar-akar (penyelesaian) persamaan kuadrat dengan faktorisasi (pemfaktoran). - Menentukan akarakar persamaan kuadrat dengan pemfaktoran, melengkapkan bentuk kuadrat sempurna, dan rumus abc. Tugas Uraian kelompok. singkat. - Dengan menggunakan rumus abc, tentukan akar-akar persamaan kuadrat berikut: 2 × 45 menit a. x2 2x p 0 Sumber: Buku paket hal. 69-72, 7275, 75-78. Buku referensi lain. b. 2x2 ( p 2) x 3 0 - Mencari akar-akar persamaan kuadrat dengan melengkapkan bentuk kuadrat sempurna. Alat: - Laptop - LCD - OHP - Mencari akar-akar persamaan kuadrat dengan menggunakan rumus abc. - Pertidaksa maan kuadrat dan penyelesaian nya. - Mendeskripsikan bentuk umum dan contoh pertidaksamaan kuadrat. - Menentukan penyele-saian pertidaksamaan kuadrat. - Menemukan arti geometris dari penyelesaian pertidaksamaan kuadrat menggunakan grafik fungsi kuadrat. - Menentukan himpunan penyelesaian pertidaksamaan kuadrat. Kuis. Uraian obyektif. - Tentukan penyelesaian pertidaksamaan berikut. a. 3x2 x2 11x 5 b. x2 2x 6 0 2 × 45 menit Sumber Buku paket hal. 79-83. Buku referensi lain. c. 2x2 3x 4 0 Alat: - Laptop - LCD - OHP - Mendeskripsikan tafsiran geometris dari penyelesaian persamaan dan pertidaksamaan kuadrat. - Menyelesaikan pertidaksamaan kuadrat dengan menggunakan metode titik uji. - Pengertian fungsi. - Fungsi aljabar sederhana dan kuadrat. - Grafik fungsi alja-bar sederhana dan fungsi kuadrat. - Persamaan kuadrat dan penyelesaiannya. - Melakukan ulangan - Mengerjakan soal Ulangan berisi materi yang dengan baik berkaitan harian. berkaitan dengan dengan materi pengertian fungsi, mengenai pengertian fungsi aljabar fungsi, fungsi aljabar sederhana dan sederhana dan kuadrat, kuadrat, grafik fungsi grafik fungsi aljabar aljabar sederhana dan sederhana dan fungsi fungsi kuadrat, serta kuadrat, serta penyelesaian dari penyelesaian dari persamaan dan persamaan dan pertidaksamaan pertidaksamaan kuadrat. kuadrat. Pilihan ganda. 1. Salah satu akar persamaan 2 × 45 menit x2 mx 4 0 adalah -2, maka nilai m = ..... a. -4 d. 4 b. -2 e. 6 Uraian obyektif. - c. 2 2. Tentukan himpunan penyelesaian persamaan kuadrat berikut. Pertidaksamaa n kuadrat dan penyelesaiann ya. a. x2 25 0 b. 3x2 x 2 0 - Diskriminan persamaan kuadrat. - Mengidentifikasi hubungan antara jenis akar persamaan kuadrat dan nilai diskriminan. - Merumuskan - Menggunakan diskriminan dalam pemecahan masalah persamaan kuadrat. Tugas individu . Uraian obyektif. - Persamaan x2 (m 1) x 2m 1 0 mempunyai dua akar tidak nyata, maka nilai m adalah...... 2 × 45 menit Sumber: Buku paket hal. 83-85. Buku referen si hubungan antara jenis akar persamaan kuadrat dan nilai diskriminan. lain. Alat: - Laptop - Menyelidiki jenis akar persamaan kuadrat dengan menghitung diskriminan persamaan kuadrat. - Rumus jumlah dan hasil kali akar-akar persamaan kuadrat. - Menghitung jumlah dan hasil kali akar persamaan kuadrat dari hasil penyelesaian persamaan kuadrat. - LCD - OHP - Menggunakan rumus jumlah dan hasil kali akar-akar persamaan kuadrat. Kuis. Uraian obyektif. - Jika p dan q adalah akar - akar persamaan kuadrat 1 × 45 menit 2 x bx 6 0 , tentukan nilai-nilai dari: - Menentukan hubungan antara jumlah dan hasil kali akar dengan koefisien persamaan kuadrat. Buku paket hal. 86-89. Buku referen si lain. a. p q b. pq Alat: c. p 2q pq 2 - Laptop - LCD d. p 2 q 2 - Merumuskan hubungan antara jumlah dan hasi kali akar dengan koefisien persamaan kuadrat. Sumber: - OHP - Membuktikan rumus jumlah dan hasil kali akar persamaan kuadrat. - Menggunakan rumus jumlah dan hasil kali akar persamaan kuadrat dalam perhitungan. - Hubungan antara koefisien - Mengidentifikasi hubungan antara koefisien - Menentukan sifat akar dari persamaan kuadrat berdasarkan Tugas Uraian singkat. - Tentukan sifat akar dari persamaan 1 × 45 menit Sumber: Buku paket persamaan kuadrat dengan sifat akar. persamaan kuadrat dengan sifat akar. koefisien persamaan kuadrat. individ u. kuadrat berikut. hal. 89-91. Buku referen si lain. 2 a. 5x x 15 0 - Menentukan sifat akar dari persamaan kuadrat berdasarkan koefisien persamaan kuadrat yang diketahui. b. 7x2 x 7 0 Alat: - Laptop - LCD - OHP 2.4. Melakukan manipulasi aljabar dalam perhitungan yang berkaitan dengan persamaan dan pertidaksamaan kuadrat. - Penyusunan persamaan kuadrat yang akar-akarnya diketahui. Mandiri Kreatif - Penyelesaian persamaan lain yang berkaitan dengan persamaan kuadrat. Rasa ingin tahu Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan - Menyusun - Menyusun persamaan persamaan kuadrat kuadrat yang akaryang diketahui akarnya diketahui akar-akarnya, yaitu serta menentukan dengan penyelesaian menggunakan persamaan yang perkalian faktor dapat dibawa ke atau menggunakan bentuk persamaan rumus jumlah dan atau pertidaksamaan hasil kali akar-akar. kuadrat. - Menyusun persamaan kuadrat yang akar- akarnya mempunyai hubungan dengan akar - akar persamaan kuadrat lainnya. - Mengenali persamaanpersamaan yang dapat diubah ke dalam persamaan kuadrat. - Menyelesaikan persamaan yang dapat dibawa ke bentuk persamaan atau pertidaksamaan Tugas kelompok . Uraian obyektif. - Akar-akar persamaan 2 x 2x 3 0 adalah x1 dan x2 . Persamaan kuadrat baru yang akar akarnya x1 3 dan x2 3 adalah..... 2 × 45 menit Sumber: Buku paket hal. 91-92, 9293, 93-96. Buku referen si lain. Alat: - Laptop - LCD - OHP kuadrat. - Diskriminan persamaan kuadrat. - Rumus jumlah dan hasil kali akar-akar persamaan kuadrat. - Hubungan antara koefisien persamaan kuadrat dengan sifat akar. - Penyusunan persamaan kuadrat yang akar-akarnya diketahui. - Melakukan ulangan berisi materi yang berkaitan dengan diskriminan persamaan kuadrat, rumus jumlah dan hasil kali akar-akar persamaan kuadrat, hubungan antara koefisien persamaan kuadrat dengan sifat akar, penyusunan persamaan kuadrat yang akar- akarnya diketahui, penyelesaian persamaan lain yang berkaitan dengan persamaan kuadrat. - Mengerjakan soal dengan baik berkaitan dengan materi mengenai diskriminan, rumus jumlah dan hasil kali akar-akar persamaan kuadrat, hubungan antara koefisien persamaan kuadrat dengan sifat akar, penyusunan persamaan kuadrat yang akar-akarnya diketahui, penyelesaian persamaan lain yang berkaitan dengan persamaan kuadrat. Ulangan harian. Pilihan ganda. 2 × 45 menit a. x2 x 30 0 b. x2 x 30 0 c. x2 x 30 0 d. x2 30x 1 0 e. x2 30x 1 0 Uraian obyektif. 2. Fungsi kuadrat dengan persamaan y px2 4x 4 akan merupakan definit positif, jika nilai p adalah....... - Penyelesaian persamaan lain yang berkaitan dengan persamaan kuadrat. - Penentuan persamaan kurva dari sebuah fungsi kuadrat dengan ciri ciri tertentu. 1. Persamaan kuadrat yang akar-akarnya -5 dan 6 adalah....... - Menentukan persamaan kurva jika diketahui titik baliknya. - Menentukan persamaan kurva jika diketahui titik potongnya dengan - Menentukan persamaan kurva dari suatu fungsi kuadrat. Tugas kelompok . Uraian singkat. Persamaan grafik pada gambar adalah ......... 2 × 45 menit Sumber: Buku paket hal. 103-107. Buku referen si lain. sumbu X. - Menentukan persamaan kurva dari sebuah fungsi jika diketahui 3 titik yang dilalui parabola. 2.5. Merancang model matematika dari masalah yang berkaitan dengan persamaan dan / atau fungsi kuadrat. - Penggunaan persamaan dan fungsi kuadrat dalam penyelesaian masalah. Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan - Mengidentifikasi masalah sehari-hari yang mempunyai keterkaitan dengan persamaan dan fungsi kuadrat. - Menentukan besaran masalah yang dirancang sebagai variabel persamaan atau fungsi kuadrat. - Merumuskan persamaan atau fungsi kuadrat yang merupakan model matematika dari suatu masalah dalam matematika, mata pelajaran lain, atau kehidupan sehari-hari. - Menyelesaikan model matematika dari suatu masalah dalam matematika, mata pelajaran lain, atau kehidupan sehari - hari yang berkaitan dengan persamaan atau Alat: - Mengidentifikasi masalah yang berkaitan dengan persamaan dan fungsi kuadrat, menentukan besaran masalah tersebut sebagai variabel, membuat model matematikanya, menyelesaikan modelnya, dan menafsirkan hasil penyelesaian masalah tersebut. Tugas kelompok . Uraian singkat. - Persamaan parabola yang grafiknya melalui titik (0, 2), (2, 4), dan (3, 8) adalah........ 2 × 45 menit - Laptop - LCD - OHP Sumber: Buku paket hal. 108-110. Buku referensi lain. Alat: - Laptop - LCD - OHP 2.6.Menyelesaikan model matematika dari masalah yang berkaitan dengan persamaan dan/atau fungsi kuadrat dan penafsirannya. - Penentuan persamaan kurva dari sebuah fungsi kuadrat dengan ciri ciri tertentu. - Penggunaan persamaan dan fungsi kuadrat dalam penyelesaian masalah. Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan fungsi kuadrat. Uraian - Menafsirkkan penyelesaian masalah dalam matematika, mata pelajaran lain, atau kehidupan sehari hari yang berkaitan dengan persamaan atau fungsi kuadrat. - Melakukan ulangan berisi materi yang berkaitan dengan penentuan persamaan kurva dari sebuah fungsi kuadrat dengan ciri-ciri tertentu dan penggunaan persamaan dan fungsi kuadrat dalam penyelesaian masalah. obyektif. - Mengerjakan soal dengan baik berkaitan dengan materi mengenai penentuan persamaan kurva dari sebuah fungsi kuadrat dengan ciri-ciri tertentu dan penggunaan persamaan dan fungsi kuadrat dalam penyelesaian masalah. Ulangan harian. - Tentukan penyelesaian dari persamaan parabola yang grafiknya melalui titik (0, 2), (2, 4), dan (3, 8). Pilihan ganda. 1. Suatu kawat yang panjangnya 38 cm dibengkokkan membentuk persegi panjang yang luasnya 84 cm2. Panjang persegi panjang yang terbentuk adalah........ Uraian obyektif a. 22 cm cm d. 7 b. 21 cm cm e. 5 c. 12 cm 2. Tentukan sumbu simetri, titik puncak, sifat definit positif atau negatif dari fungsi kuadrat berikut ini. a. f ( x) x 2 2x 3 b. f ( x) x 2 x 2 c. f ( x) 2x2 x 2 2 × 45 menit ....………………………………… Mengetahui, Guru Mata Pelajaran Matematika Kepala Sekolah __________________ _________________ NIP/NIK. NIP/NIK. SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : X / UMUM Semester : GANJIL Sandar Kompetensi: 3. Memecahkan masalah yang berkaitan dengan sistem persamaan linear dan pertidaksamaan satu variabel. Penilaian Kompetensi Dasar 3.1. Menyelesaikan sistem persamaan linear dan sistem persamaan campuran linear dan kuadrat dalam dua variabel Materi Ajar Nilai Budaya Dan Karakter Bangsa - Sistem Persamaan Linear dan Kuadrat. - Sistem persamaan linear dua variabel. Rasa ingin tahu Kewirausahaan/ Ekonomi Kreatif Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan Kegiatan Pembelajaran - Mengidentifikasi langkah - langkah penyelesaian sistem persamaan linear dua variabel. Indikator Pencapaian Kompetensi - Menentukan penyelesaian sistem persamaan linear dua variabel. - Menggunakan sistem persamaan linear dua variabel untuk menyelesaikan soal. - Menentukan penyelesaian sistem persamaan linear dua variabel. Teknik Bentuk Instrumen Tugas individu. Uraian singkat. Alokasi Waktu Contoh Instrumen 1. Tentukan himpunan penyelesaian dari sistem persamaan linear berikut: 3x 4 y 24 2 x 5 y 23 - Memberikan tafsiran geometri dari penyelesaian sistem persamaan (menit) 4 × 45 menit Sumber / Bahan / Alat Sumber: Buku paket (Buku Matematika SMA dan MA ESIS Kelas X Semester Ganjil Jilid 1A, karangan Sri Kurnianings ih, dkk) hal. 126-130, 130-132, 133, 134138. Buku referensi lain. linear dua variabel. - Menentukan tafsiran geometri dari penyelesaian sistem persamaan linear dua variabel. - Sistem persamaan linear tiga variabel. - Mengidentifikasi langkah- langkah penyelesaian sistem persamaan linear tiga variabel. Alat: - Laptop - LCD - OHP - Menentukan Tugas penyelesaian sistem kelompok. persamaan linear tiga variabel. Uraian singkat. - Menggunakan sistem persamaan linear tiga variabel untuk menyelesaikan soal. - Tentukan himpunan penyelesaian dari sistem persaman linear berikut: 2 × 45 menit - Sistem persamaan linear dua variabel. Sistem persamaan linear tiga variabel. - Melakukan - Mengerjakan ulangan berisi soal dengan materi yang baik berkaitan berkaitan dengan dengan materi penyelesaian dari mengenai sistem persamaan penyelesaian linear dua variabel dari sistem dan sistem persamaan persamaan linear linear dua tiga variabel. variabel dan sistem persamaan linear tiga variabel. x 3y z 3 x 2 y 3 z 2 x y z 1 Ulangan harian. Pilihan ganda. 1. Himpunan penyelesaian sistem persamaan 3x 4 y 24 2 x 5 y 23 adalah x, y . Nilai dari 5x 3 y ..... Uraian obyektif. 2. Himpunan Buku paket hal. 138144. Buku referensi lain. Alat: - Menentukan penyelesaian sistem persamaan linear tiga variabel. - Sumber: 2 × 45 menit - Laptop - LCD - OHP penyelesaian sistem persamaan x 2y z 4 2 x y 3z 6 3x y 2 z 0 adalah x, y, z . Nilai dari xyz .... - Sistem persamaan linear dan kuadrat dua variabel. - Mengidentifikasi langkah - langkah penyelesaian sistem persamaan linear dan kuadrat dua variabel. - Menentukan penyelesaian sistem persamaan linear dan kuadrat dua variabel dengan menggunakan grafik. - Memeriksa hasil penyelesaian sistem persamaan linear dan kuadrat dua variabel berdasarkan grafik, dengan menggunakan metode eliminasi substitusi. - Menentukan penyelesaian sistem persamaan linear dan kuadrat dua variabel. Tugas individu. Uraian obyektif. - Nilai y yang memenuhi sistem persamaan: x 2 y 2 9 x 5 adalah…. 2 × 45 menit Sumber: Buku paket hal. 144148. Buku referensi lain. Alat: - Laptop - LCD - OHP - Sistem persamaan kuadrat (pengayaan). - Mengidentifikasi langkah- langkah penyelesaian sistem persamaan kuadrat dua variabel. - Menentukan penyelesaian sistem persamaan kuadrat dua variabel. Kuis. Uraian obyektif. - Himpunan penyelesaian sistem persamaan: 2 × 45 menit Buku paket hal. 148152. Buku referensi lain. 2 y x 3x 2 y 6x 2x adalah - Menentukan penyelesaian sistem persamaan kuadrat dua variabel. Sumber: x1, y1 ; x2 , y2 Alat: - Laptop , maka nilai dari x1 y1 x2 y2 .... - LCD - OHP - Sistem persamaan linear dan bentuk aljabar berderajat dua dengan dua variabel (pengayaan). - Menentukan penyelesaian sistem persamaan linear dan bentuk aljabar berderajat dua dengan dua variabel. - Menyelesaikan sistem persamaan linear dan bentuk aljabar berderajat dua dengan dua variabel. Tugas individu. Uraian singkat. - Tentukan himpunan penyelesaian dari sistem persamaan: x2 xy y 2 46 x 2 y 1 2 × 45 menit Sumber: Buku paket hal. 153156. Buku referensi lain. Alat: - Laptop - LCD - OHP 3.2.Merancang model matematika dari masalah yang berkaitan dengan sistem persamaan linear. - Penerapan sistem persamaan linear dua dan tiga variabel. Rasa ingin tahu Mandiri Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan - Mengidentifikasi masalah seharihari yang berhubungan dengan sistem persamaan linear. - Mengidentifikasi masalah yang berhu-bungan dengan sistem persamaan linear, Tugas kelompok. Uraian obyektif. - Dua orang anak berbelanja di sebuah toko. Anak pertama 2 × 45 menit Sumber: Buku paket hal. 125, 134-138 Buku Kerja keras - Menentukan besaran dari suatu masalah dalam matematika, mata pelajaran lain atau kehidupan seharihari yang berhubungan dengan sistem persamaan linear, yang dirancang sebagai variabel sistem persamaan linearnya. - Merumuskan model matematika dari suatu masalah dalam matematika, mata pelajaran lain atau kehidupan seharihari yang berhubungan dengan sistem persamaan linear. 3.3.Menyelesaikan model matematika dari masalah yang berkaitan dengan sistem persamaan linear dan penafsirannya. Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan - Menyelesaikan model matematika dari suatu masalah dalam matematika, mata pelajaran lain atau kehidupan seharihari yang berhubungan dengan sistem persamaan linear. - Menafsirkan penyelesaian masalah dalam matematika, mata pelajaran lain atau kehidupan seharihari yang menentukan besaran dari masalah tersebut sebagai variabel, membuat model matematikanya, menyelesaikan modelnya, dan menafsirkan hasil penyelesaian masalah tersebut. membayar Rp7.450,00 untuk membeli 3 pensil dan 2 buku tulis, sedangkan anak kedua harus membayar Rp11.550,00 untuk membeli 5 pensil dan 3 buku tulis. Maka harga pensil per buah adalah..... referensi lain. Alat: - Laptop - LCD - OHP berhubungan dengan sistem persamaan linear. - Sistem persamaan linear dan kuadrat dua variabel. - Melakukan ulangan berisi materi yang berkaitan dengan sistem persamaan linear dan kuadrat dua variabel, sistem persamaan kuadrat, sistem persamaan linear dan bentuk aljabar berderajat dua dengan dua variabel, serta penerapan sistem persamaan linear dua dan tiga variabel. - Sistem persamaan kuadrat. - Sistem persamaan linear dan bentuk aljabar berderajat dua dengan dua variabel. Penerapan sistem persamaan linear dua dan tiga variabel. 3.4. Menyelesaikan pertidaksamaan satu variabel yang melibatkan bentuk pecahan aljabar. Pertidaksamaan. - Pertidaksamaan linear. Rasa ingin tahu Mandiri Kreatif - Pertidaksa maan satu variabel berbentuk pecahan aljabar (pecahan bentuk linear dan kuadrat) Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan - Mengidentifikasi langkah-langkah penyelesaian pertidaksamaan yang memuat bentuk linear satu variabel. - Menggunakan pertidaksamaan yang memuat bentuk linear satu variable untuk menyelesaikan - Mengerjakan soal dengan baik berkaitan dengan materi menge-nai sistem persamaan linear dan kuadrat dua variabel, sistem persamaan kuadrat, sistem persamaan linear dan bentuk aljabar berderajat dua dengan dua variabel, serta penerapan sistem persamaan linear dua dan tiga variabel. Ulangan harian. Pilihan ganda. - Himpunan penyelesaian sistem persamaan: y 1 x 2 y x 4 x 5 adalah x1, y1 ; x2 , y2 , maka nilai dari x1 y1 x2 y2 .... a. -8 d. 0 b. -6 e. 2 c. -2 - Menjelaskan Tugas individu. Uraian singkat. 1. Nilai x yang sifat dan aturan memenuhi yang digunakan dalam proses pertidaksama penyelesaian an pertidaksamaan. 3x 2 5x 14 adalah… - Menentukan 2 × 45 menit 4 × 45 menit Sumber: Buku paket hal. 164168, 168171, 172174 Buku referensi lain. Alat: soal. - Menentukan penyelesaian pertidaksamaan yang memuat bentuk linear satu variabel. penyelesaian pertidaksamaan satu variabel yang melibatkan bentuk pecahan aljabar (pecahan bentuk linear dan kuadrat). - Mengidentifikasi langkah - langkah penyelesaian pertidaksamaan satu variabel yang melibatkan bentuk pecahan aljabar (pecahan bentuk linear dan kuadrat). - Laptop - LCD - OHP 2. Nilai x yang memenuhi pertidaksama an 5 7 x7 x5 adalah… - Menggunakan pertidaksamaan satu variabel yang melibatkan bentuk pecahan aljabar (pecahan bentuk linear dan kuadrat) untuk menyelesaikan soal. - Menentukan penyelesaian pertidaksamaan yang memuat bentuk linear satu variabel yang melibatkan bentuk pecahan aljabar (bentuk linear dan kuadrat). - Pertidaksa maan bentuk akar. - Menentukan penyelesaian pertidaksamaan yang memuat bentuk akar. - Menentukan penyelesaian pertidaksamaan bentuk akar dan bentuk nilai mutlak. Tugas Uraian singkat. 1. Nilai x kelompok. yang memenuhi pertidaksama 2 × 45 menit Sumber: Buku paket hal. 175177, 179182 - Pertidaksa-maan bentuk nilai mutlak. 3.5.Merancang model matematika dari masalah yang berkaitan dengan pertidaksamaan satu variabel. - Penerapan kon-sep pertidaksamaan satu variabel dalam menyelesaikan masalah nyata. an - Menentukan penyelesaian pertidaksamaan yang memuat nilai mutlak. Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan - Mengidentifikasi masalah yang berhubungan dengan pertidaksamaan satu variabel. - Menentukan besaran dari suatu masalah dalam matematika, mata pelajaran lain atau kehidupan sehari-hari yang berhubungan dengan pertidaksamaan satu variabel, yang dirancang sebagai variabel pertidaksamaan satu variabelnya. - Merumuskan model matematika dari suatu masalah dalam matematika, mata pelajaran lain atau Buku referensi lain. 4x 8 2 adalah… Alat: 2. Tentukan himpunan penyelesaian dari pertidaksama an 3x 6 3 . - Mengidentifikasi masalah yang berhubungan dengan pertidaksamaan satu variabel, menentukan besaran dari masalah tersebut sebagai variabel, membuat model matematikanya, menyelesaikan modelnya, dan menafsirkan hasil penyelesaian masalah tersebut. Tugas kelompok. Uraian singkat. - Jumlah dari dua biangan ganjil berurutan lebih dari 21. Tentukanlah nilai dari bilangan yang terbesar dari kedua bilangan tersebut. 2 × 45 menit - Laptop - LCD - OHP Sumber: Buku paket hal. 183185. Buku referensi lain. Alat: - Laptop - LCD - OHP 3.6. Menyelesaikan model matematika dari masalah yang berkaitan dengan pertidaksamaan satu variabel dan penafsirannya. Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri kehidupan seharihari yang berhubungan dengan pertidaksamaan satu variabel. Keorisinilan - Menyelesaikan model matematika dari suatu masalah dalam matematika, mata pelajaran lain atau kehidupan seharihari yang berhubungan dengan pertidaksamaan satu variabel. - Menafsirkan penyelesaian masalah dalam matematika, mata pelajaran lain atau kehidupan seharihari yang berhubungan dengan pertidaksamaan satu variabel. - Pertidaksa maan linear. - Pertidaksa maan satu variabel berbentuk pecahan aljabar (pecahan bentuk linear dan kuadrat) - Pertidaksamaan - Melakukan ulangan berisi materi yang berkaitan dengan pertidak-samaan linear, pertidaksamaan pecahan (pecahan bentuk linear dan kuadrat), pertidaksamaan bentuk akar, pertidaksamaan - Mengerjakan soal dengan baik berkaitan dengan materi mengenai pertidaksa-maan linear, pertidaksamaan pecahan (pecahan bentuk linear dan kuadrat), pertidak-samaan bentuk akar, Ulangan harian. Pilihan ganda. 1. Nilai x yang memenuhi pertidaksama an 2 2 × 45 menit x 3 4 x 3 12 adalah....... a. 2 x 9 b. bentuk akar. - Pertidaksamaan bentuk nilai mutlak. - Penerapan konsep pertidaksamaa n satu variabel dalam menyelesaikan masalah nyata. bentuk nilai mutlak, dan penerapan konsep pertidaksama-an satu variabel dalam menyelesaikan masalah nyata. 3 x 9 pertidaksamaan bentuk nilai mutlak, dan penerapan konsep pertidak-samaan satu variabel dalam menyelesaikan masalah nyata. c. x 9 atau x 1 d. x 9 atau x 2 Uraian singkat. e. x 9 atau x 3 2. Tentukan himpunan penyelesaian dari pertidaksama an berikut: a. 3x2 7x 2 0 b. 3x2 9x x2 4 c. d. x 1 x 3 x 1 e. x2 2x 3x 6 f. 9 x 12 3 Mengetahui, Guru Mata Pelajaran Matematika Kepala Sekolah __________________ _________________ NIP/NIK. NIP/NIK. SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran : Matematika Satuan Pendidikan : SMA / MA Kelas/Semester : X/2 Nama Guru NIP/NIK Sekolah : ........................... : ........................... : ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : X / UMUM Semester : GENAP STANDAR KOMPETENSI: 4. Menggunakan logika matematika dalam pemecahan masalah yang berkaitan dengan pernyataan majemuk dan pernyataan berkuantor. Penilaian Kompetensi Materi Dasar Ajar Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran Indikator Pencapaian Kompetensi Teknik Bentuk Instrumen Contoh Alokasi Waktu Sumber / (menit) Alat Bahan / Instrumen 4.1. Memahami pernyataan dalam matematika dan ingkaran atau negasinya. Logika Matematika. Rasa ingin tahu - Pernyataan dan Mandiri nilai Kreatif kebenarannya. Kerja keras - Kalimat terbuka dan Demokratis himpunan penyelesaian nya. Berorientasi tugas dan hasil Percaya diri Keorisinilan - Membedakan antara kalimat pernyataan (disebut juga pernyataan) dan kalimat terbuka. - Menentukan nilai kebenaran dari suatu pernyataan. - Menentukan himpunan penyelesaian dari kalimat terbuka. - Menjelaskan arti dan contoh dari pernyataan dan kalimat terbuka, serta menentukan nilai kebenaran suatu pernyataan. Tes lisan. Tanya jawab. - Sebutkan beberapa contoh kalimat terbuka dan kalimat pernyataan. 1 x 45 menit Sumber: - Buku paket (Buku Matema tika SMA dan MA ESIS Kelas X Semeste r Genap Jilid 1B, karanga n Sri Kurnian ingsih, dkk) hal. 2-4. - Buku referens i lain. Alat: - Ingkaran atau negasi dari suatu pernyataan dan nilai kebenarannya. - Menentukan ingkaran atau negasi suatu pernyataan. - Menentukan ingkaran atau negasi dari suatu pernyataan beserta nilai kebenarannya. Kuis. Uraian singkat.. - Tentukan ingkaran atau negasi dari pernyataan: 1 x 45 menit a. p: 3 + 4 = 7 - Menentukan nilai kebenaran dari ingkaran suatu pernyataan. ~p: b. p: Semua bilangan prima Nilai kebenaran dari pernyataan majemuk: Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan - Konjun gsi Kerja keras - Disjun gsi - Implik asi - Mengidentifikasi pernyataan seharihari yang mempunyai keterkaitan dengan pernyataan majemuk. Demokratis - Mengidentifikasi kakteristik pernyataan majemuk berbentuk konjungsi, - Menentukan nilai kebenaran dari suatu pernyataan majemuk berbentuk konjungsi, disjungsi, implikasi, dan biimplikasi. Tugas kelompok. Uraian singkat. - Tentukan nilai kebenaran dari konjungsi “Garis y 2x 3 melalui titik (1, 2) dan (2, 1)!“. - LCD - OHP Sumber: - Buku paket hal. 4-6. Alat: ~p: .............................. - Laptop - Buku referens i lain. adalah bilangan ganjil. 4.2. Menentukan nilai kebenaran dari suatu pernyataan majemuk dan pernyataan berkuantor. - 2 x 45 menit - Laptop - LCD - OHP Sumber: - Buku paket hal. 617, 21-23. - Buku refere nsi lain. - Biimpli kasi disjungsi, implikasi, dan iimplikasi. Alat: - Merumuskan nilai kebenaran dari pernyataan majemuk berbentuk konjungsi, disjungsi, implikasi, dan biimplikasi dengan tabel kebenaran. - Laptop - LCD - OHP - Menentukan nilai kebenaran dari pernyataan majemuk berbentuk konjungsi, disjungsi, implikasi, dan biimplikasi. - Ingkaran (negasi) dari pernyataan majemuk: - Konjungsi - Disjungsi - Implikasi - Merumuskan ingkaran atau negasi dari pernyataan majemuk berbentuk konjungsi, disjungsi, implikasi, dan biimplikasi dengan tabel kebenaran. - Biimplikasi - Menentukan ingkaran atau negasi dari pernyataan majemuk berbentuk konjungsi, disjungsi, implikasi, dan biimplikasi. - Menentukan ingkaran atau negasi dari suatu pernyataan majemuk berbentuk konjungsi, disjungsi, implikasi, dan biimplikasi. Kuis Uraian singkat. - Tentukan negasi dari: 2 x 45 menit Sumber: - Buku paket hal. 26-30. - Buku refere nsi lain. a. Jika 2 + 3 > 4, maka 4 = 2 2 (B) b. Jika guru matematika tidak datang, maka semua siswa senang. Alat: - Laptop - LCD - OHP - Konvers, invers, kontraposisi. - Mengidentifikasi hubungan antara implikasi dengan konvers, invers, dan kontraposisi. - Menentukan konvers, invers, dan kontraposisi dari pernyataan berbentuk implikasi. - Menentukan konvers, invers, dan kontraposisi dari pernyataan berbentuk implikasi beserta nilai kebenarannya. Tugas individu. Uraian obyektif. Nilai kebenaran dari pernyataan berkuantor dan ingkaranny a. - Menjelaskan arti kuantor universal dan kuantor eksistensial beserta ingkarannya. Tentukan konvers, invers, dan kontraposisi dari implikasi berikut, kemudian tentukan nilai kebenarannya! 2 x 45 menit Sumber - - b. Jika x 3 , maka x = 3. - Menentukan nilai kebenaran dan ingkaran dari suatu pernyataan berkuantor. Tugas individu. Uraian singkat. - Tentukan nilai kebenaran pernyataan pernyataan berikut. - Mengubah kalimat terbuka menjadi pernyataan dengan menambah kuantor pada kalimat terbuka. - Menentukan nilai kebenaran pernyataan x R x 2 x Buku refere nsi lain. Alat: 2 x 45 menit - Laptop - LCD - OHP Sumber - Buku paket hal. 33-38. a. - Memberikan contoh pernyataan yang mengandung kuantor universal atau eksistensial. Buku paket hal. 31-32. a. Jika x 600 , maka 1 sin x 0 3. 2 - Menentukan nilai kebenaran dari implikasi, konvers, invers, dan kontraposisi. - - - b. y Z 3 y 4 Buku refere nsi lain. Alat: - Laptop - LCD - OHP berkuantor. - Menentukan ingkaran (negasi) dan pernyataan berkuantor universal atau eksistensial. - Menentukan ingkaran pernyataan berkuantor yang mengandung sekaligus beberapa kuantor. - Pernyataan. - Kalimat terbuka. - Ingkaran (negasi) pernyataan. - - Melakukan ulangan berisi materi yang berkaitan dengan pernyataan, kalimat terbuka, ingkaran (negasi) pernyataan, nilai kebenaran pernyataan majemuk dan ingkarannya, konvers, invers, kontraposisi, serta nilai kebenaran pernyataan berkuantor dan ingkarannya. Nilai kebenaran pernyataan majemuk dan ingkarannya. - Konvers, Invers, Kontraposisi. - Nilai kebenaran - Mengerjakan soal dengan baik berkaitan dengan materi mengenai pernyataan, kalimat terbuka, ingkaran (negasi) pernyataan, nilai kebenaran pernyataan majemuk dan ingkarannya, konvers, invers, kontraposisi, serta nilai kebenaran pernyataan berkuantor dan ingkarannya. Ulangan harian. Pilihan ganda. 1. Kontraposisi dari implikasi ~ pq adalah…… a. ~ q p d. q p b. ~ p q Uraian obyektif. e. q ~ p c. a. (~ p q) ~ q b. ( p q) q berkuantor dan c. ~ ( p q) ~ q ingkarannya. - Bentuk ekuivalen p q 2. Tentukan nilai kebenaran dari: Pernyataan 4.3. Merumuskan pernyataan yang setara 2 x 45 menit Rasa ingin tahu Berorientasi tugas dan hasil - Mengidentifikasi pernyataan majemuk yang setara - Memeriksa atau membuktikan Tugas individu. Uraian obyektif. - Selidiki apakah dua pernyataan majemuk berikut 2 x 45 menit Sumber: - Buku dengan pernyataan majemuk atau pernyataan antara dua pernyataan majemuk. Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis berkuantor yang diberikan. - Tautologi dan kontradiksi. (ekuivalen). - Memeriksa atau membuktikan kesetaraan antara dua pernyataan majemuk atau pernyataan berkuantor dengan sifat-sifat logika matematika. - Mengidentifikasi karakteristik dari pernyataan tautologi dan kontradiksi dari tabel nilai kebenaran. - Memeriksa apakah suatu pernyataan majemuk merupakan suatu tautologi atau kontradiksi atau bukan keduanya. kesetaraan antara dua pernyataan majemuk atau pernyataan berkuantor. ekuivalen. a. paket ( p ~ q) hal. 2425. dan - (~ q p ) b. ( p q) dan (q p) Alat: - Menyelidiki apakah suatu pernyataan majemuk merupakan suatu tautologi, kontradiksi, bukan tautologi, atau bukan kontradiksi. Tugas kelompok. Uraian singkat. - Selidikilah dengan menggunakan tabel kebenaran bentuk pernyataan majemuk berikut, apakah merupakan tautologi, kontradiksi, bukan tautologi, atau bukan kontradiksi. 2 x 45 menit ( p q) p b. ~ ( p q) ( p q) Kesetaraan (ekuivalens i) dari dua pernyataan majemuk. - Melakukan ulangan berisi materi yang berkaitan dengan kesetaraan (ekuivalensi) dari dua pernyataan - Mengerjakan soal dengan baik berkaitan dengan materi mengenai kesetaraan (ekuivalensi) dua Ulangan harian. Pilihan ganda. 1. Pernyataan “jika turun hujan, maka jalanan macet“ ekuivalen dengan....... - Laptop - LCD - OHP Sumber: - Buku paket hal. 18-20. - Buku refere nsi lain. Alat: a. - Buku refere nsi lain. 2 x 45 menit - Laptop - LCD - OHP - Tautologi dan majemuk, tautologi, dan kontradiksi. kontradiksi. pernyataan majemuk, tautologi, dan kontradiksi. a. Jika tidak turun hujan, maka jalanan tidak macet. Uraian obyektif. b. Jika jalanan macet, maka turun hujan. c. Hujan turun atau jalanan macet. d. Tidak turun hujan tetapi jalanan macet. e. Tidak turun hujan atau jalanan macet. 2. Selidikilah apakah pernyataan majemuk berikut merupakan tautologi atau bukan. a. ( p ~ q) q b. p (q ~ q) 4.4. Menggunakan prinsip logika matematika yang berkaitan dengan - Penarikan kesimpulan : - Prinsip modus ponens Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras - Mengidentifikasi cara- cara penarikan kesimpulan dari beberapa contoh yang diberikan. - Menentukan kesimpulan dari beberapa premis yang diberikan dengan prinsip modus ponens, modus tolens, dan Tugas individu. Uraian singkat. 1. Berdasarkan prinsip modus tolens, tentukan kesimpulan dari premis - premis berikut ini. 4 x 45 menit Sumber: - Buku paket hal. 38-44. - Buku - Prinsip modus tolens pernyataan majemuk dan pernyataan berkuantor dalam penarikan kesimpulan dan pemecahan masalah. - Prinsip silogis me Demokratis - Merumuskan cara penarikan kesimpulan berdasarkan implikasi silogisme. refere nsi lain. p1 : Jika Budi lulus ujian, maka ia pergi rekreasi. (prinsip modus ponens, modus tolens, dan silogisme). Alat: p2 : Budi tidak pergi rekreasi. _________ - Laptop - LCD - OHP …………… - Memeriksa keabsahan dari penarikan kesimpulan. - Menyusun kesimpulan yang sah berdasarkan premis premis yang diberikan. - Memeriksa keabsahan penarikan kesimpulan menggunakan prinsip logika matematika. 2. Tulislah kesimpulan yang sah dari premis premis yang diberikan dalam bentuk lambang berikut: . a. p1 : p ~q p2 : ~ q b. p1 : p ~q p2 : p Penyusuna n bukti (pengayaan ). - Mengenal karakteristik atau keunggulan dari teknik-teknik penyusunan bukti, yaitu antara bukti langsung, bukti tak langsung, dan induksi matematika. - Menyusun bukti - Membuktikan sebuah persamaan atau pernyataan dengan bukti langsung, bukti tak langsung, atau induksi matematika. Tugas individu. Uraian obyektif. - Buktikan dengan menggunakan induksi matematika bahwa 1 2 3 4 2 x 45 menit Sumber: - Buku paket 1 hal. n n (n 1) 2 44-49. - Buku refere nsi lain. sebuah persamaan atau pernyataan dengan bukti langsung, bukti tak langsung, atau dengan induksi matematika sesuai langkah langkahnya. - Penarikan kesimpulan berdasarkan prinsip modus ponens, modus tolens, atau silogisme beserta keabsahannya . Penyusuna n bukti dengan bukti - Melakukan ulangan berisi materi yang berkaitan dengan penarikan kesimpulan berdasarkan prinsip modus ponens, modus tolens, atau silogisme beserta keabsahannya, serta penyusunan bukti (bukti langsung, bukti tak langsung, atau induksi matematika). Alat: - Mengerjakan soal dengan baik berkaitan dengan materi mengenai penarikan kesimpulan berdasarkan prinsip modus ponens, modus tolens, atau silogisme beserta keabsahannya, serta penyusunan bukti (bukti langsung, bukti tak langsung, atau induksi matematika). Ulangan harian. Pilihan ganda. 1. Diketahui premis premis: (1) (2) p ~q ~p q q ~p ~p q (3) ~p q ~p q langsung, bukti tak langsung, atau induksi matematik a. Prinsip penarikan kesimpulan di atas yang sah adalah...... a. hanya (1) b. hanya (2) c. hanya (1) dan (2) Uraian obyektif. d. hanya (2) dan (3) e. (1), (2), (3) 2 x 45 menit - Laptop - LCD - OHP 2. Selidikilah sah atau tidaknya penarikan kesimpulan berikut. p1 : Jika PQRS adalah jajargenjang, maka PQ sejajar SR. p1 : PQRS bukan jajargenjang. ________________ PQ tidak sejajar SR. ....………………………………… Mengetahui, Guru Mata Pelajaran Matematika Kepala Sekolah __________________ __________________ NIP/NIK. NIP/NIK. SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : X / UMUM Semester : GENAP STANDAR KOMPETENSI: 5. Menggunakan perbandingan, fungsi, persamaan, dan identitas trigonometri dalam pemecahan masalah. Penilaian Kompetensi Materi Dasar Ajar 5.1. Melakukan manipulasi aljabar dalam perhitungan teknis yang berkaitan dengan perbandingan, fungsi, persamaan, dan identitas trigonometri. Trigonometri. - Perbandingan trigonometri pada segitiga siku - siku. Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Kegiatan Pembelajaran - Menjelaskan arti derajat dan radian. - Menghitung perbandingan sisi sisi segitiga sikusiku yang sudutnya tetap tetapi panjang sisinya berbeda. - Mengidentifikasikan pengertian perbandingan trigonometri pada segitiga siku-siku. Indikator Pencapaian Kompetensi - Menentukan nilai perbandingan trigonometri (sinus, kosinus, tangen, kotangen, sekan, dan kosekan suatu sudut) pada segitiga siku siku. Teknik Tugas individu. Bentuk Instrumen Uraian singkat. Contoh Instrumen - Tentukan nilai perbandingan trigonometri untuk sudut θ pada gambar: 24 26 θ Alokasi Waktu Sumber / (menit) Alat 2 x 45 menit Bahan / Sumber: - Buku paket (Buku Matemat ika SMA dan MA ESIS Kelas X Semester Genap Jilid 1B, karangan Sri Kurniani ngsih, dkk) hal. 6069. - Menentukan nilai perbandingan trigonometri suatu sudut (sinus, kosinus, tangen, kotangen, sekan, dan kosekan suatu sudut) pada segitiga siku siku. Buku referensi lain. Alat: - Laptop - LCD - OHP - Perbandingan trigonometri sudut - sudut khusus. - Menyelidiki nilai perbandingan trigonometri (sinus, kosinus, dan tangen) dari sudut khusus. - Menentukan nilai perbandingan trigonometri (sinus, kosinus, dan tangen) dari sudut khusus. Tugas individu. Uraian singkat. Hitunglah nilai 0 sin 30 dan cos 30 0 2 x 45 menit tan 30 0 . Apakah yang diperoleh? - Menggunakan nilai perbandingan trigonometri (sinus, kosinus, dan tangen) dari sudut khusus dalam menyelesaikan soal. - Perbandingan trigonometri dari sudut di semua kuadran. - Menurunkan rumus perbandingan trigonometri (sinus, kosinus, dan tangen) suatu sudut pada bidang Cartesius. - Melakukan perhitungan nilai perbandingan trigonometri pada Sumber: - Buku paket hal. 7073. - Buku referensi lain. Alat: - Menentukan nilai perbandingan trigonometri (sinus, kosinus, dan tangen) dari sudut di semua kuadran. Tugas kelompok. Uraian obyektif. - Tentukan nilai x yang memenuhi persamaan: sin ( x 200 ) 3 , x 0, 2 2 2 x 45 menit - Laptop - LCD - OHP Sumber: - Buku paket hal. 7380. - Buku referensi lain. Alat: - Laptop bidang Cartesius. - Menyelidiki hubungan antara perbandingan trigonometri dari sudut di berbagai kuadran (kuadran I, II, III, IV). - Menentukan nilai perbandingan trigonometri dari sudut di berbagai kuadran. - Perbandingan trigonometri pada segitiga siku-siku. - Perbandingan trigonometri sudut-sudut khusus. - Perbandingan trigonometri dari sudut di semua kuadran. - Melakukan ulangan berisi materi yang berkaitan dengan perbandingan trigonometri pada segitiga siku-siku, perbandingan trigonometri sudut-sudut khusus, dan perbandingan trigonometri dari sudut di semua kuadran. - Mengerjakan soal dengan baik berkaitan dengan materi mengenai perbandingan trigonometri pada segitiga siku-siku, perbandingan trigonometri sudut -sudut khusus, dan perbandingan trigonometri dari sudut di semua kuadran. Ulangan harian. Pilihan ganda. 1. Himpunan penyelesaian persamaan 1 sin x 2, 2 untuk 0 x 2 adalah…… a. π 4 3 d. , 4 4 3 b. 4 5 e. , 4 4 Uraian obyektif. 5 c. 4 2 x 45 menit - LCD - OHP 2. Tentukan nilai dari: a. sin1500 b. cos 2400 c. tan 3150 - Persamaan trigonometri sederhana. - Menentukan besarnya suatu sudut yang nilai sinus, kosinus, dan tangennya diketahui. - Menyelesaikan persamaan trigonometri sederhana. Tugas individu. Uraian obyektif. - Tentukan nilai x yang memenuhi persamaan berikut pada interval Menggunakan tabel nilai perbandingan trigonometri dan kalkulator untuk mencari nilai perbandingan trigonometri. - Buku paket hal. 8184. - Buku referensi lain. 1 2 b. tan 2x 1 - Menentukan penyelesaian persamaan trigonometri sederhana. - Sumber: , . a. cos x - Penggunaan tabel dan kalkulator untuk mencari nilai perbandingan trigonometri. 2 x 45 menit Alat: - Menggunakan tabel dan kalkulator untuk menentukan nilai pendekatan fungsi trigonometri dan besar sudutnya. Tugas individu. Uraian singkat. - Dengan menggunakan kalkulator, tentukan nilai: 2 x 45 menit - Laptop - LCD - OHP Sumber: - Buku paket hal. 8588. - Buku referensi lain. a. cos34,50 d. cos1 0,69590 b. tan1250 e. sin 1 0, 42740 Alat: c. sin 750 - Laptop f. sec130 0 - Pengambaran grafik fungsi trigonometri. - - Menyimak pemahaman tentang langkahlangkah menggambar grafik fungsi trigonometri dengan menggunakan tabel dan lingkaran satuan. - Menggambar grafik fungsi trigonometri dengan menggunakan tabel dan lingkaran satuan. Tugas kelompok. Uraian obyektif. - Buatlah sketsa grafik fungsi fungsi berikut pada interval 1800 , 1800 2 x 45 menit a. y sin ( x 300 ) - LCD - OHP Sumber: - Buku paket hal. 8995. - Buku referensi lain. b. y cos ( x 600 ) c. y 1 sin 2x Alat: Menggunakan rumus sinus dan kosinus dalam penyelesaian soal. - Laptop - LCD - OHP - Mengkonstruksi gambar grafik fungsi sinus dan kosinus. - - Koordinat kutub (pengayaan). Menggambarkan grafik fungsi tangen. - Menjelaskan pengertian koordinat kutub. - Memahami langkah langkah - Mengubah koordinat kutub ke koordinat Cartesius, dan sebaliknya. Kuis Uraian singkat. - Ubahlah koordinat kutub berikut ke dalam bentuk koordinat Cartesius. 2 x 45 menit Sumber: - Buku paket hal. 9598. - Buku referensi a. A (4, 300 ) menentukan koordinat kutub suatu titik. - - Persamaan trigonometri sederhana. - Penggunaan tabel dan kalkulator untuk mencari nilai perbandingan trigonometri. - Pengambaran grafik fungsi trigonometri. - Koordinat kutub. - c. C (6, 210o ) d. Mengidentifikasi hubungan antara koordinat kutub dan koordinat Cartesius. Melakukan ulangan berisi materi yang berkaitan dengan persamaan trigonometri sederhana, penggunaan tabel dan kalkulator untuk mencari nilai perbandingan trigonometri, pengambaran grafik fungsi trigonometri, dan koordinat kutub. lain. b. B (5, 1350 ) - Mengerjakan soal dengan baik berkaitan dengan materi mengenai persamaan trigonometri sederhana, penggunaan tabel dan kalkulator untuk mencari nilai perbandingan trigonometri, pengambaran grafik fungsi trigonometri, dan koordinat kutub. Ulangan harian. Pilihan ganda. 1. Himpunan penyelesaian persamaan 3 tan x 1 0 , untuk 0 x 2 adalah…… a. 6 5 d. , 6 6 7 b. 6 7 e. , 6 6 Uraian Alat: D (3, 450 ) 5 c. 6 singkat. 2. Ubahlah koordinat titik berikut ke dalam koordinat kutub, kemudian tunjukkan pada satu bidang gambar. a. A(2, 2) b. B(2, 2 3) 2 x 45 menit - Laptop - LCD - OHP c. C(6, 6) d. D( 3, 1) e. E(3, 3 3) - Hubungan antar perbandingan trigonometri suatu sudut (identitas trigonometri dan pembuktiannya) 5.2. Merancang model matematika dari masalah yang berkaitan dengan perbandingan, fungsi, persamaan, dan identitas - Aturan sinus, aturan kosinus, dan rumus luas segitiga. - Menggunakan identitas trigonometri dalam penyelesaian soal. - Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Merumuskan hubungan antara perbandingan trigonometri suatu sudut. - Membuktikan identitas trigonometri sederhana dengan menggunakan rumus hubungan antara perbandingan trigonometri. - Mengidentifikasi permasalahan dalam perhitungan sisi atau sudut pada segitiga. - Membuktikan dan menggunakan identitas trigonometri sederhana dalam penyelesaian soal. Tugas kelompok. Uraian singkat. - Buktikan identitas identitas berikut. 2 x 45 menit Menggunakan aturan sinus, aturan kosinus, dan rumus luas segitiga dalam penyelesaian soal. - Buku paket hal. 98104. - Buku referensi lain. a. 8sin 2 A 8cos 2 A 8 b. 4sin 2 A 4 4cos2 A c. (1 tan2 A)cos2 A 1 d. sinA cot AcosA cosecA - Sumber: Tugas individu. Uraian singkat. - Diketahui segitiga ABC dengan sisi Alat: 2 x 45 menit - Laptop - LCD - OHP Sumber: - Buku paket hal. 104108. - Buku referensi lain. a = 2, c = 4, dan cos A 7 . Jika 8 segitiga tersebut bukan segitiga sama kaki, maka panjang sisi b adalah...... trigonometri. - Merumuskan aturan sinus dan aturan kosinus. Alat: - Menggunakan aturan sinus dan aturan kosinus untuk menyelesaikan soal perhitungan sisi atau sudut pada segitiga. 5.3 Menyelesaikan model matematika dari masalah yang berkaitan dengan perbandingan, fungsi, persamaan, dan identitas trigonometri, - Pemakaian perbandingan trigonometri. Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan - Mengidentifikasi permasalahan dalam perhitungan luas segitiga. - Menurunkan rumus luas segitiga. - Menggunakan rumus luas segitiga untuk menyelesaikan soal. - Mengidentifikasi masalah yang berkaitan dengan perbandingan, fungsi, persamaan, dan identitas trigonometri. Kerja keras Demokratis - Menentukan Mengidentifikas i masalah yang berkaitan dengan perbandingan, fungsi, persamaan, dan identitas trigonometri, menentukan Tugas individu. Uraian singkat. - Sebuah perahu berlayar meninggalkan pelabuhan ke arah timur dengan jarak 20 mil. Kemudian belok ke arah 150o dari utara dengan jarak 15 mil. Jarak perahu ke pelabuhan 2 x 45 menit - Laptop - LCD - OHP Sumber: - Buku paket hal. 104108. - Buku referensi lain. dan penafsirannya. besaran dari suatu masalah yang dirancang sebagai variabel yang berkaitan dengan ekspresi trigonometri. - besaran dari masalah tersebut sebagai variabel, membuat model matematikanya, menyelesaikan modelnya, dan menafsirkan hasil penyelesaian masalah tersebut. Merumuskan model matematika dari masalah yang berkaitan dengan fungsi trigonometri, adalah...... Alat: - Laptop - LCD - OHP rumus sinus, dan rumus kosinus. - Menentukan penyelesaian dari model matematika. - Memberikan tafsiran terhadap penyelesaian dari masalah. - Menjelaskan dan mendeskripsikan sudut elevasi dan sudut depresi. Sumber: - Sudut elevasi dan sudut depresi (pengayaan). - Menentukan sudut elevasi dan sudut depresi. - Menggunakan sudut elevasi dan depresi dalam penyelesaian - Menggunakan sudut elevasi dan depresi dalam penyelesaian masalah. Tugas kelompok. Uraian obyektif. - Rafif mengamati bahwa sudut elevasi dari gedung di depannya adalah 35o. Jika tinggi gedung 30 m dan tinggi Rafif 170 cm, tentukan jarak rafif terhadap gedung itu. 2 x 45 menit - Buku paket hal.109112. - Buku referensi lain. Alat: - Laptop - LCD masalah. - Identitas trigonometri dan pembuktiannya . - Aturan sinus, aturan kosinus, dan rumus luas segitiga. - Pemakaian perbandingan trigonometri. - Sudut elevasi dan sudut depresi. - Melakukan ulangan berisi materi yang berkaitan dengan identitas trigonometri dan pembuktiannya, aturan sinus, aturan kosinus, dan rumus luas segitiga, pemakaian perbandingan trigonometri, serta sudut elevasi dan sudut depresi. - - Mengerjakan soal dengan baik berkaitan dengan materi mengenai identitas trigonometri dan pembuktianny a, aturan sinus, aturan kosinus, dan rumus luas segitiga, pemakaian perbandingan trigonometri, serta sudut elevasi dan sudut depresi. Ulangan harian. Pilihan ganda. 1. Segitiga ABC dengan besar A 3000 , 2 x 45 menit B 600 0 , dan panjang sisi a = 4 cm. Luas segitiga ABC tersebut adalah……… a. 6 cm2 d. 16 cm2 Uraian b. 12 cm2 e. 16 3 cm2 obyektif. c. 8 3 cm2 2. Diketahui segitiga ABC merupakan segitiga sama sisi dengan panjang sisi 10 cm, tentukan luas segitiga ABC tersebut. ....………………………………… Mengetahui, Guru Mata Pelajaran Matematika Kepala Sekolah __________________ __________________ NIP/NIK. NIP/NIK. OHP SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : X / UMUM Semester : GENAP STANDAR KOMPETENSI: 6. Menentukan kedudukan, jarak, dan besar sudut yang melibatkan titik, garis, dan bidang dalam ruang dimensi tiga. Penilaian Kompetensi Materi Dasar Ajar Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran Indikator Pencapaian Kompetensi Teknik Bentuk Instrumen Contoh Alokasi Waktu Sumber / (menit) Alat Bahan / Instrumen 6.1. Menentukan kedudukan, jarak, dan besar sudut yang melibatkan titik, garis, dan bidang dalam ruang dimensi tiga. Ruang Dimensi Tiga. - Titik, garis, dan bidang. Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis - Kedudukan titik, garis, dan bidang pada bangun ruang. Berorientasi tugas dan hasil Percaya diri Keorisinilan - Mengidentifikasi bentuk - bentuk bangun ruang. - Mengidentifikasi unsur - unsur bangun ruang. - Menentukan kedudukan titik terhadap garis dalam ruang. - Menentukan kedudukan titik terhadap bidang - Menentukan kedudukan titik, garis, dan bidang dalam ruang. Tugas individu. Uraian singkat. - Pada kubusABCD.EFG H: a. 4 x 45 menit Sumber: - Buku paket (Buku Matematik a SMA dan MA ESIS Kelas X Semester Genap Jilid 1B, karangan Sri Kurnianing sih, dkk) hal. 126-127, 127-132. - Buku AB tegak lurus pada bidang BCGF sebab....... b. AB sejajar HG sebab........ c. AC tegak lurus pada bidang BDHF sebab......... dalam ruang. referensi lain. - Menentukan kedudukan dua garis dalam ruang. Alat: - Menentukan kedudukan garis dan bidang dalam ruang. - Laptop - LCD - OHP - Menentukan kedudukan dua bidang dalam ruang. - Menentukan perpotongan lebih dari dua bidang dalam ruang. - Luas permukaan dan volume bangun ruang. - Menentukan luas permukaan dan volume bangun ruang (prisma, limas, kerucut, tabung, bola). - Menjelaskan penerapan rumus-rumus volume dan luas permukaan bangun ruang. - Menentukan luas permukaan dan volume bangun ruang. - Menjelaskan penerapan rumus-rumus volume dan luas permukaan bangun ruang. Tugas individu. Uraian singkat. - Panjang diagonal sisi suatu kubus adalah 16 cm. Volume kubus tersebut adalah........... 4 x 45 menit Sumber: - Buku paket hal. 132134, 135-137, 137-138, 139-140, 140-141, 142-144. - Buku referensi lain. Alat: - Laptop - Proyeksi. - Menentukan proyeksi titik pada bidang. - Menentukan proyeksi titik dan garis pada bidang. Tugas individu. Uraian singkat. bangun ruang. - Menjelaskan bidang gambar, bidang frontal, bidang ortogonal. - Menjelaskan garis frontal dan garis ortogonal. - Menjelaskan sudut surut (sudut menyisi). - Menjelaskan perbandingan proyeksi dalam menggambarkan bangun ruang. - Menggambarkan 2 x 45 menit a. Tentukan proyeksi BE dan CH pada bidang ABCD. - Menentukan proyeksi garis pada bidang. - Menggambar - Diketahui balok ABCD.EFGH. b. Tentukan proyeksi BE pada BDHF. - Menjelaskan bidang frontal, bidang ortogonal, garis frontal, garis ortogonal, sudut surut, dan perbandingan proyeksi dalam menggambarkan bangun ruang. Tugas individu. Uraian singkat. - Lukislah sebuah limas segiempat beraturan T.ABCD yang memiliki panjang alas 4 cm dan tinggi 3 cm, dengan bidang TBD sebagai bidang frontal dan sudut surut 120o. - LCD - OHP Sumber: - Buku paket hal. 145147. - Buku referensi lain. Alat: 2 x 45 menit - Laptop - LCD - OHP Sumber: - Buku paket hal. 147151. - Buku referensi lain. Alat: - Laptop - LCD - OHP bangun ruang. - Titik, garis, dan bidang. - Kedudukan titik, garis, dan bidang pada bangun ruang. - Luas permukaan dan volume bangun ruang. - Proyeksi. - Melakukan ulangan berisi materi yang berkaitan dengan titik, garis, dan bidang, kedudukan titik, garis, dan bidang pada bangun ruang, luas permukaan dan volume bangun ruang, proyeksi, dan penggambaran bangun ruang. - Mengerjakan soal dengan baik berkaitan dengan materi mengenai titik, garis, dan bidang, kedudukan titik, garis, dan bidang pada bangun ruang, luas permukaan dan volume bangun ruang, proyeksi, dan penggambaran bangun ruang. Ulangan harian. Pilihan ganda. 1. Diketahui kubus ABCD.EFGH. Dari pasangan pasangan garis: 2 x 45 menit (1) DG dan CH (2) AG dan CE (3) EF dan CF (4) DF dan CH Pasangan garis yang saling bersilangan adalah nomor… a. 4 b. 2 dan 4 - Menggambar c. 1 dan 3 bangun ruang. d. 1, 2, dan 3 e. 1, 2, 3, dan 4 Uraian obyektif. 2. Diketahui kubus ABCD.EFGH yang panjang rusuk rusuknya adalah 10 cm. Tentukanlah: a. panjang diagonal sisinya. b. Panjang diagonal ruangnya. 6.2. Menentukan jarak dari titik ke garis dan dari titik ke bidang - Jarak pada bangun ruang. Rasa ingin tahu Mandiri Kreatif Berorientasi tugas dan hasil Percaya diri - Mendefinisikan pengertian jarak antara titik, garis, dan bidang - Menentukan jarak titik ke titik, jarak titik ke garis, jarak titik ke Tugas individu. Uraian obyektif. - Pada bidang empat beraturan T.ABC dengan panjang rusuk 6 cm, jarak antara titik T dan 4 x 45 menit Sumber: - Buku paket hal. 152157. Kerja keras dalam ruang dimensi tiga. Keorisinilan dalam ruang. bidang, jarak antara dua garis sejajar, jarak antara dua garis yang bersilangan, dan jarak antara garis dan bidang yang sejajar dalam ruang. Demokratis - Menggambar dan menghitung jarak titik ke titik pada bangun ruang. - Menggambar dan menghitung jarak titik ke garis pada bangun ruang. bidang ABC adalah..... - Buku referensi lain. Alat: - Laptop - LCD - OHP - Menggambar dan menghitung jarak titik ke bidang pada bangun ruang. - Menggambar dan menghitung jarak antara dua garis sejajar pada bangun ruang. - Menggambar dan menghitung jarak antara dua garis yang bersilangan pada bangun ruang. - Menggambar dan menghitung jarak antara garis dan bidang yang sejajar pada bangun ruang. 6.3. Menentukan besar sudut - Sudut - sudut dalam ruang. Rasa ingin tahu Berorientasi - Mendefinisikan pengertian sudut - Menentukan besar sudut Tugas individu. Uraian singkat. - Pada kubus ABCD.EFGH 4 x 45 menit Sumber: - Buku paket Mandiri antara garis dan bidang dan antara dua bidang dalam ruang dimensi tiga. tugas dan hasil Kreatif Percaya diri Kerja keras Keorisinilan Demokratis antara titik, garis, dan bidang dalam ruang. - Menggambar dan menghitung sudut antara dua garis pada bangun ruang. antara dua garis, besar sudut antara garis dan bidang, dan besar sudut antara dua bidang dalam ruang. dengan sudut antara BG dan bidang BDE adalah . Nilai sin =..... hal. 158160, 160-161, 161-164. - - Menggambar dan menghitung sudut antara garis dan bidang pada bangun ruang. Buku referensi lain. Alat: - Laptop - LCD - OHP - Menggambar dan menghitung sudut antara dua bidang pada bangun ruang. - Menggambar irisan bangun ruang. - Melukis bidang datar pada bangun ruang. - Melukis garis potong dua bidang pada bangun ruang. - Melukis titik tembus garis dan bidang pada bangun ruang. - Menjelaskan pengertian dari bidang irisan dan - Menggambar irisan suatu bidang dengan bangun ruang. Tugas individu. Uraian obyektif. - Pada kubus ABCD.EFGH dengan panjang rusuk 8 cm, titik P pada AE dengan perbandingan AP : PE = 3 : 1. Luas bidang irisan yang melalui BP dan sejajar FG dengan kubus adalah..... 4 x 45 menit Sumber: - Buku paket hal. 164172. - Buku referensi lain. Alat: - Laptop - LCD - OHP sumbu afinitas. - Melukis bidang irisan dengan menggunakan sumbu afinitas. - Melukis bidang irisan dengan menggunakan diagonal ruang. - Jarak pada bangun ruang. - Sudut-sudut dalam ruang. - Menggambar irisan bangun ruang. - Melakukan ulangan berisi materi yang berkaitan dengan penentuan jarak pada bangun ruang, sudutsudut dalam ruang, dan penggambaran irisan bangun ruang. - Mengerjakan soal dengan baik berkaitan dengan materi mengenai penentuan jarak pada bangun ruang, sudut-sudut dalam ruang, dan penggambara n irisan bangun ruang. Ulangan harian. Pilihan ganda. 1. Pada kubus ABCD.EFGH dengan panjang rusuk 2a cm, jarak antara EF dan bidang ABGH adalah..... a. 1 a 2 cm 2 b. a 2 cm c. 2a 2 cm d. 1 a 3 cm 2 e. a 3 cm Uraian singkat. 2. Diketahui bidang empat D.ABC dengan DB = DC = 5 cm, AD = BC = 6 cm, dan AB = AC = 34 cm. Sudut antara bidang ABC dan bidang BCD adalah , maka 2 x 45 menit nilai cos adalah……. ....………………………………… Mengetahui, Guru Mata Pelajaran Matematika Kepala Sekolah __________________ __________________ NIP/NIK. NIP/NIK. SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran : Matematika Satuan Pendidikan : SMA / MA Kelas/Semester : XI/1 Nama Guru NIP/NIK Sekolah : ........................... : ........................... : ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : XI / IPA Semester : GANJIL STANDAR KOMPETENSI: 1.Menggunakan aturan statistika, kaidah pencacahan, dan sifat-sifat peluang dalam pemecahan masalah. Kompetensi Dasar 1.1. Membaca data dalam bentuk tabel dan diagram batang, garis, lingkaran, dan ogif. Materi Ajar Statistika. Data: - Jenis-jenis data. - Ukuran data. Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Disiplin Kerja keras Demokratis Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Berani mengambil resiko Keorisinilan Statistika dan statistik. Mengamati dan mengidentifik asi data-data mengenai hal-hal di sekitar sekolah. - Pemeriksaan Memahami cara-cara memperoleh data. Menentukan jenis data, ukuran data. Populasi dan sampel. Data tunggal: Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Memahami pengertian statistika, Memahami cara memperoleh data, menentukan jenis dan ukuran data, serta memeriksa, membulatkan, dan menyusun data untuk menyelesaikan masalah. Menentukan data terbesar, terkecil, median, kuartil (kuartil pertama, kuartil kedua, kuartil ketiga), statistik Penilaian Teknik Tugas individu. Bentuk Instrumen Uraian singkat. Contoh Instrumen Nilai Matematika dari 10 siswa adalah 3, 7, 6, 5, 7, 9, 8, 4, 7, 8. Alokasi Waktu Sumber /Bahan / (menit) Alat 2 x 45 menit. Sumber: Buku paket (Buku Matematika SMA dan MA ESIS Kelas XI Semester 1 Jilid 2A, karangan Sri Kurnianings ih,dkk) hal. 2-6, 6-7, 7-16. Buku referensi lain. Tentukan: a. Kuartil pertama, kuartil kedua, dan kuartil ketiga. b. Rataan kuartil dan rataan tiga. c. Jangkauan, jangkauan antar-kuartil, dan jangkauan semi antarkuartil. Alat: data. statistik, populasi, dan sampel. - Pembulatan data. - Penyusunan data. - Data terbesar, terkecil, dan median. - Kuartil (kuartil pertama, kuartil kedua, kuartil ketiga). - Statistik lima serangkai (statistik minimum, statistik maksimum, median, kuartil pertama, kuartil ketiga). - Rataan kuartil dan rataan tiga. - Desil. - Jangkauan. - Jangkauan antar-kuartil. - Jangkauan semi antarkuartil (simpangan kuartil). Melakukan penanganan awal data tunggal berupa pemeriksaan data, pembulatan data, penyusunan data, serta pencarian data terbesar, data terkecil, median, kuartil (kuartil pertama, kuartil kedua, kuartil ketiga), statistik lima serangkai (statistik minimum, statistik maksimum, median, kuartil pertama, kuartil ketiga), rataan kuartil, rataan tiga, desil, jangkauan, jangkauan antar-kuartil, dan jangkauan semi antarkuartil. lima serangkai (statistik minimum, statistik maksimum, median, kuartil pertama, kuartil ketiga), rataan kuartil, rataan tiga, desil, jangkauan, jangkauan antarkuartil, dan jangkauan semi antar-kuartil untuk data tunggal. Laptop LCD OHP Tabel (daftar) baris-kolom. Daftar distribusi frekuensi. Daftar distribusi frekuensi kumulatif. Membaca datadata yang dinyatakan dalam bentuk daftar bariskolom, daftar distribusi frekuensi data tunggal, daftar distribusi frekuensi data berkelompok, daftar distribusi frekuensi kumulatif data tunggal, atau daftar distribusi frekuensi kumulatif data berkelompok. Membaca sajian data dalam bentuk tabel (daftar), meliputi daftar baris-kolom, daftar distribusi frekuensi (data tunggal dan data berkelompok), dan daftar distribusi frekuensi kumulatif (data tunggal dan data berkelompok). Tugas individu. Uraian singkat. 2 x 45 menit. Daftar bariskolom berikut menyatakan banyaknya anak laki-laki dan perempuan yang dimiliki oleh suatu keluarga yang mengikuti survei. Sumber: Buku paket hal. 17-18, 18-19, 2223, 24-26. Buku referensi lain. Alat: Ba ny ak an ak Banyak anak laki-laki 0 1 2 3 4 pe re mp ua n 0 3 1 5 9 2 1 2 3 1 2 1 1 3 2 4 a. Berapa banyak keluarga yang mengikuti survei? b. Berapa banyak keluarga yang memiliki anak laki-laki? c. Berapa banyak anak laki-laki dan perempuan yang terdaftar? Laptop LCD OHP d. Apakah pernyataan ini benar “Anak laki-laki lebih banyak dillahirkan dibandingkan anak perempuan“. Jelaskan! Diagram garis. Diagram kotak-garis. Diagram batang daun. Diagram batang dan diagram lingkaran. Histogram dan poligon frekuensi. Diagram campuran. Ogif. Membaca datadata yang dinyatakan dalam bentuk diagram garis, diagram kotakgaris, diagram batang daun, diagram batang dan diagram lingkaran, histogram, poligon frekuensi, diagram campuran, dan ogif. Membaca sajian data dalam bentuk diagram, meliputi diagram garis, diagram kotak-garis, diagram batang-daun, diagram batang dan diagram lingkaran, histogram, poligon frekuensi, diagram campuran, dan ogif. Tugas individu. Uraian singkat. Misalkan garis berikut menunjukkan curah hujan ratarata per bulan di Indonesia (dalam milimeter) yang tercatat di Badan Meteorologi dan Geofisika. 4 x 45 menit. Sumber: Buku paket hal. 29-30, 31-32, 3233, 3538, 39-40, 40-41. Buku referensi lain. Alat: a. Sebutkan bulan yang paling basah dan bulan yang paling kering. b. Berapa mmkah curah hujan rata-rata pada bulan April? c. Sebutkan bulan-bulan dengan curah Laptop LCD OHP hujan lebih dari 150 mm. 1.2. Menyajik an data dalam bentuk tabel dan diagram batang, garis, lingkaran, dan ogif, serta penafsiran - nya. Penyajian data dalam bentuk tabel (daftar): Rasa ingin tahu Mandiri Kreatif - Tabel (daftar) baris-kolom. Disiplin Kerja keras - Daftar distribusi Demokratis frekuensi. - Daftar distribusi frekuensi kumulatif. Berorientasi tugas dan hasil Menyimak konsep tentang penyajian data. Percaya diri Menyusun / menyajikan data dalam bentuk tabel, yang meliputi: Berani mengambil resiko Keorisinilan a. b. Penyajian data dalam bentuk diagram: - Diagram garis. - Diagram kotak-garis. - Diagram batang daun. - Diagram batang dan diagram lingkaran. - Histogram dan poligon frekuensi. - Diagram campuran. - Ogif. c. Daftar bariskolom. Daftar distribusi frekuensi (data tunggal dan data berkelom pok). Daftar distribusi frekuensi kumulatif (data tunggal dan data berkelom pok). Menyusun / menyajikan data dalam bentuk diagram, yang meliputi: a. Diagram garis. b. Diagram kotak- Menyajikan Tugas data dalam individu. berbagai bentuk tabel, meliputi daftar bariskolom, daftar distribusi frekuensi (data tunggal dan data berkelompok), dan daftar distribusi frekuensi kumulatif (data tunggal dan data berkelompok). Menyajikan data dalam berbagai bentuk diagram, meliputi diagram garis, diagram kotak-garis, diagram batang daun, diagram batang, diagram lingkaran, histogram, poligon frekuensi, diagram campuran, dan ogif. Uraian singkat. 1. Data nilai Matematika di kelas XI IPA adalah sebagai berikut: 4 x 45 menit. 6 7 5 4 9 5 4 4 5 6 5 37 4 8 5 9 6 4 5 7 6 6 5 6 4 6 87 8 9 3 6 7 4 5 6 6 6 8 a. Susun data di atas dalam daftar distribusi frekuensi data tunggal. b. Tentukan frekuensi kumulatif kurang dari dan lebih dari. 2. Buatlah diagram batang daun dari data berikut: 88 84 47 52 43 28 63 73 30 32 58 76 61 68 21 64 56 34 78 51 35 63 50 31 73 57 74 66 74 69 50 48 78 24 67 45 52 64 34 49 81 27 56 64 74 68 33 55 70 29 Sumber: Buku paket hal. 17-29, 29-44. Buku referensi lain. Alat: Laptop LCD OHP garis. c. Diagram batang daun. d. Diagram batang. e. Diagram lingkaran. f. Histogram. g. Poligon frekuensi. h. Diagram campuran. i. Ogif. Menafsirkan data dari berbagai macam bentuk tabel dan diagram. Menafsirkan data dari berbagai macam bentuk tabel dan diagram. Pengertian dasar statistika: data (jenis-jenis data, ukuran data), statistika dan statistik, populasi dan sampel, serta data tunggal. Penyajian data dalam bentuk tabel (daftar): tabel (daftar) bariskolom, daftar distribusi frekuensi, daftar distribusi Melakukan ulangan berisi materi yang berkaitan dengan pengertian dasar statistika (data (jenis-jenis data, ukuran data), statistika, statistik, populasi, sampel, data tunggal), penyajian data dalam bentuk tabel (daftar baris-kolom, daftar distribusi Mengerjakan soal dengan baik berkaitan dengan materi mengenai pengertian dasar statistika (data (jenisjenis data, ukuran data), statistika, statistik, populasi, sampel, data tunggal), penyajian data dalam bentuk tabel (daftar baris- Ulangan harian. Uraian singkat. Gambarlah histogram dan poligon frekuensi untuk data hasil ulangan Bahasa Inggris dari 40 siswa berikut: Nilai Frekue nsi 46-50 3 51-55 5 56-60 7 61-65 10 66-70 8 2 x 45 menit. frekuensi kumulatif. 1.3. Menghitu ng ukuran pemusata n, ukuran letak, dan ukuran penyebara n data, serta penafsiran nya. frekuensi, daftar distribusi frekuensi kumulatif), dan penyajian data dalam bentuk diagram (diagram garis, diagram kotakgaris, diagram batang daun, diagram batang, diagram lingkaran, histogram, poligon frekuensi, diagram campuran, dan ogif). Penyajian data dalam bentuk diagram:, diagram garis, diagram kotak-garis, diagram batang daun, diagram batang dan diagram lingkaran, histogram dan poligon frekuensi, diagram campuran, ogif. Ukuran pemusatan data: Rasa ingin tahu - Rataan. Kreatif - Modus. Kerja keras - Median. Demokratis Mandiri Berorientasi tugas dan hasil Percaya diri Keorisinilan Menjelaskan pengertian ukuran pemusatan data. Mendefinisik an rataan dan macamnya (rataan data tunggal, rataan sementara data tunggal, rataan data berkelompok, rataan sementara data berkelompok) kolom, daftar distribusi frekuensi, daftar distribusi frekuensi kumulatif), dan penyajian data dalam bentuk diagram (diagram garis, diagram kotak-garis, diagram batang daun, diagram batang, diagram lingkaran, histogram, poligon frekuensi, diagram campuran, dan ogif). Menentukan ukuran pemusatan data, meliputi rataan (rataan data tunggal, rataan sementara data tunggal, rataan data berkelompok, rataan sementara data berkelompok, pengkodean atau coding data berkelompok), modus, dan . Tugas individu. Uraian singkat. 71-75 4 76-80 3 Tentukan modus, median, dan rata-rata dari data berikut: Data f 40-44 4 45-49 8 4 x 45 menit. Sumber: Buku paket hal. 44-48, 48-50, 5052, 5255, 56-60, 60-63. Buku referensi lain. 50-54 6 55-59 14 60-64 8 Alat: 65-69 6 Laptop 70-74 4 LCD OHP , median (untuk data tunggal maupun data berkelompok) , dan modus (untuk data tunggal maupun data berkelompok) sebagai ukuran pemusatan data yang biasa digunakan. Menentukan rumus rataan data tunggal yang bernilai kecil. Menghitung rataan data tunggal yang bernilai kecil. Menentukan rumus rataan data tunggal yang bernilai besar dengan menggunakan rataan sementara. Menghitung rataan data tunggal dengan menggunakan rataan sementara. Menentukan rumus rataan data berkelompok. median. Memberikan tafsiran terhadap ukuran pemusatan data. Menghitung rataan data berkelompok. Menentukan rumus rataan data berkelompok dengan menggunakan rataan sementara. Menghitung rataan data berkelompok dengan menggunakan rataan sementara. Menentukan rumus rataan data berkelompok dengan cara pengkodean (coding). Menghitung rataan data berkelompok dengan cara pengkodean (coding). Mendefinisik an modus suatu data. Menentukan rumus modus untuk data tunggal maupun data berkelompok. Menghitung modus dari data tunggal maupun data berkelompok. Ukuran pemusatan data: - Rataan. - Modus. - Median. Menentukan rumus median untuk data tunggal maupun data berkelompok. Menghitung median dari data tunggal maupun data berkelompok. Menyelesaika n soal seharihari untuk mencari ukuran pemusatan data kemudian disajikan dalam bentuk diagram dan menafsirkan hasil yang didapat. Melakukan ulangan berisi materi yang berkaitan dengan ukuran pemusatan data, yaitu rataan, modus, dan median untuk data tunggal maupun data Mengerjakan soal dengan baik berkaitan dengan materi mengenai ukuran pemusatan data, yaitu rataan, modus, dan median untuk data tunggal maupun data Ulangan harian. Uraian singkat. Tentukan rataan hitung dari data berikut dengan menggunakan rataan sementara. Berat (kg) Titik teng ah f (xi) 30-34 3 35-39 6 40-44 6 2 x 45 menit. berkelompok. Ukuran letak kumpulan data: - Kuartil. - Desil dan persentil. Ukuran penyebaran Mendefinisik an kuartil dan macamnya (kuartil bawah, kuartil tengah atau median, dan kuartil atas) untuk data berkelompok. berkelompok. Menentukan ukuran letak kumpulan data yang meliputi kuartil, desil, dan persentil. Tugas kelompok. Uraian singkat. Memahami pengertian 1 0 55-59 6 60-64 2 Hasil pengukuran tinggi badan siswa kelas XI B adalah sebagai berikut: 2 x 45 menit. Sumber: Buku paket hal. 63-65, 65-70. Buku referensi lain. f 150-154 12 155-159 25 160-164 22 165-169 36 Laptop 170-174 15 LCD 175-179 10 OHP Alat: a. Tentukan nilai P15, P85. b. Tentukan nilai D8, D4. Menghitung kuartil bawah, kuartil tengah (median), dan kuartil atas untuk data berkelompok. Menentukan desil dan persentil dari data berkelompok. 7 50-54 Tinggi Memberikan tafsiran terhadap ukuran letak kumpulan data. Menentukan rumus kuartil bawah, kuartil tengah (median), dan kuartil atas untuk data berkelompok. 45-49 c. Tentukan nilai Q1, Q2, Q3.. Menentukan ukuran Tugas Uraian Hasil ulangan Matematika 4 x 45 menit. Sumber: data: dan rumus dari jangkauan, jangkauan antar-kuartil, dan simpangan kuartil. - Jangkauan. - Simpangan kuartil. - Simpangan rata-rata. - Ragam dan simpangan baku. Menentukan jangkauan antar-kuartil dan simpangan kuartil pada distribusi frekuensi yang diketahui. Mendefinisik an pencilan (data yang tidak konsisten dalam kelompoknya ). Menentukan pencilan dari suatu kumpulan data. Mendefinisik an simpangan rata-rata. Menentukan simpangan rata-rata untuk data tunggal maupun simpangan rata-rata dari distribusi frekuensi penyebaran data, meliputi jangkauan, simpangan kuartil, simpangan rata-rata, ragam, dan simpangan baku. Menentukan data yang tidak konsisten dalam kelompoknya. Memberikan tafsiran terhadap ukuran penyebaran data. kelompok. singkat. kelas XI A sebagai berikut: 42 50 50 62 70 97 80 87 47 45 53 67 63 88 78 72 53 47 55 59 64 73 85 55 46 71 60 62 75 81 Tentukan jangkauan, simpangan kuartil, dan simpangan baku. Buku paket hal. 70-74, 74-79, 8086. Buku referensi lain. Alat: Laptop LCD OHP data berkelompok. Ukuran letak kumpulan data: kuartil, desil, dan persentil. Ukuran penyebaran data: jangkauan, simpangan kuartil, simpangan rata-rata, ragam dan simpangan baku. Mendefinisik an ragam (variansi) dan simpangan baku (deviasi standar). Menghitung dan mendapatkan ragam dan simpangan baku dari data yang diperoleh baik dari suatu populasi maupun sampel. Melakukan ulangan berisi materi yang berkaitan dengan ukuran letak kumpulan data (kuartil, desil, dan persentil) dan ukuran penyebaran data (jangkauan, simpangan kuartil, simpangan rata-rata, ragam dan simpangan Mengerjakan soal dengan baik berkaitan dengan materi mengenai ukuran letak kumpulan data dan ukuran penyebaran data. Ulangan harian. Uraian singkat. Tentukan ragam dan simpangan baku dari populasi data: 17 25 27 30 35 36 47. . 2 x 45 menit. baku). 1.4. Menggunak Peluang. an aturan Aturan perkalian, pengisian permutasi, tempat: dan kombinasi - Diagram dalam pohon. pemecahan Tabel masalah. silang. - Pasangan terurut. - Kaidah (aturan) penjumlaha n. - Rasa ingin tahu Mandiri Kreatif Disiplin Kerja keras Demokratis Berorientasi tugas dan hasil Percaya diri Berani mengambil resiko Keorisinilan Mendefinisik an kaidah pencacahan. Mengenal metode aturan pengisian tempat, metode permutasi, dan metode kombinasi sebagai tiga metode pencacahan. Mengidentifi kasi masalah yang dapat diselesaikan dengan kaidah pencacahan. Mengenal diagram pohon, tabel silang, dan pasangan terurut sebagai tiga cara pendaftaran semua kemungkinan hasil dalam aturan pengisian tempat. Menentukan berbagai kemungkinan Aturan perkalian. Menyusun aturan perkalian. Menggunakan aturan perkalian untuk menyelesaikan soal. Tugas individu. Pilihan ganda. Banyaknya bilangan ribuan ganjil yang dapat dibentuk dari angka-angka: 0, 1, 2, 3, 4 adalah..... 2 x 45 menit. Sumber: Buku paket hal.98-100, 100-101, 101-105. Buku referensi lain. a. 200 d. 300 b. 250 e. 450 Alat: c. 256 Laptop LCD OHP pengisian tempat dalam permainan tertentu atau masalahmasalah lainnya. Notasi faktorial. Menyimpulka n atau mendefinisik an aturan penjumlahan. Menyimpulka n atau mendefinisik an aturan perkalian dan penggunaann ya. Menyimpulka n atau mendefinisik an notasi faktorial dan penggunaann ya. Permutasi: - - - - Permutasi n objek dari n objek yang berbeda. Permutasi k objek dari n objek yang berbeda, k < n. Permutasi n objek dari n objek dengan beberapa objek sama. Permutasi Menyimpulka n atau mendefinisik an permutasi. Mengidentifi kasi jenisjenis permutasi. Mengidentifi kasi masalah yang dapat diselesaikan dengan permutasi. Mendefinisika n permutasi dan menggunakan permutasi dalam pemecahan soal. Tugas individu. Uraian singkat. Diketahui permutasi n P4 :n P3 9 :1 . Maka nilai n yang memenuhi adalah....... 4 x 45 menit. Sumber: Buku paket hal. 105108, 108114. Buku referensi lain. Alat: Laptop LCD OHP siklis (pengayaan ). Kombinasi: - - - Kombinasi n objek dari n objek yang berbeda. Kombinasi k objek dari n objek yang berbeda, k < n. Kombinasi k objek dari n objek dengan beberapa objek sama (pengayaan ). Binom Menggunaka n permutasi dalam penyelesaian soal. Menyimpulka n atau mendefinisik an kombinasi. Aturan Mengidentifi kasi jenisjenis kombinasi. Mendefinisika n kombinasi dan menggunakan kombinasi dalam pemecahan soal. Tugas individu. Uraian singkat. Nilai n dari kombinasi ( n 3) C 2 36 Menggunaka n kombinasi dalam penyelesaian soal. Menyimpulka n atau mendefinisik an penjabaran binom, segitiga Pascal, serta binom Newton dan penggunaann ya. Melakukan 2 x 45 menit. Sumber: Buku paket hal. 115119, 119122. Buku referensi lain. adalah...... Mengidentifi kasi masalah yang dapat diselesaikan dengan kombinasi. Newton. Alat: Mengerjakan Uraian Seorang siswa Laptop LCD OHP pengisian tempat. 1.5. Menentuka n ruang sampel suatu percobaan. Kaidah (aturan) penjumlahan. Aturan perkalian. Notasi faktorial. Permutasi Kombinasi. Binom Newton. Percobaan, ruang sampel, dan kejadian. ulangan berisi materi yang berkaitan dengan aturan pengisian tempat, kaidah (aturan) penjumlahan, aturan perkalian, notasi faktorial, permutasi, kombinasi, dan binom Newton. Rasa ingin tahu Mandiri Kreatif Disiplin Kerja keras Demokratis Berorientasi tugas dan hasil Percaya diri Berani mengambil resiko Keorisinilan Mendefinisik an percobaan, ruang sampel, titik-titik sampel (anggota ruang sampel), dan kejadian (event). Mendaftar titik-titik sampel dari suatu percobaan. Menentukan ruang sampel dari suatu percobaan. Menentukan banyaknya titik sampel. soal dengan baik berkaitan dengan materi mengenai aturan pengisian tempat, kaidah (aturan) penjumlahan, aturan perkalian, notasi faktorial, permutasi, kombinasi, dan binom Newton. Ulangan Menentukan ruang sampel suatu percobaan. Tugas individu. singkat. harian. Uraian singkat. diminta mengerjakan 4 dari 9 soal yang disediakan. Jika soal Nomor 5 harus dikerjakan, maka banyaknya pilihan soal berbeda yang akan dikerjakan siswa tersebut adalah….. 2 x 45 menit. Dari 6 ahli kimia dan 5 ahli biologi, dipilih 7 anggota untuk sebuah panitia, diantaranya 4 adalah ahli kimia. Banyaknya cara yang dapat dilakukan dalam pemilihan itu adalah…… 2 x 45 menit. Sumber: Buku paket hal. 122127. Buku referensi lain. Alat: Laptop LCD OHP 1.6. Menentuk an peluang suatu kejadian dan penafsiran nya. Peluang kejadian. Rasa ingin tahu Mandiri Kreatif Disiplin Kerja keras Demokratis Frekuensi harapan. Kejadian majemuk. Berorientasi tugas dan hasil Percaya diri Berani mengambil resiko Keorisinilan Merancang dan melakukan percobaan untuk menentukan peluang suatu kejadian. Menentukan peluang suatu kejadian dari soal atau masalah sehari-hari. Memberikan tafsiran peluang kejadian dari berbagai situasi. Mendefinisik an frekuensi harapan dan frekuensi relatif. Menggunaka n frekuensi harapan atau frekuensi relatif untuk menyelesaika n masalah. Mendefinisik an dan mengidentifik asi kejadian majemuk. Komplemen suatu kejadian. Menentukan peluang Menentukan peluang suatu kejadian dari berbagai situasi dan penafsirannya. Menggunakan frekuensi harapan atau frekuensi relatif dalam pemecahan soal dan penafsirannya. Merumuskan aturan penjumlahan dan perkalian dalam peluang kejadian majemuk dan penggunaannya. Menentukan peluang komplemen suatu kejadian dan penafsirannya. Tugas individu. Uraian singkat. 1. Dari 20 baterai kering, 5 di antaranya rusak. Jika baterai diambil satu demi satu secara acak tanpa pengembalian, maka peluang yang terambil kedua baterai rusak adalah..... 2. Empat keping uang logam diundi sekaligus. Percobaan dilakukan sebanyak 320 kali. Frekuensi harapan meunculnya tak satu pun angka adalah...... 3. Dari seperangkat kartu bridge diambil sebuah kartu. Peluang terambil kartu As atau kartu Hati adalah......... 4 x 45 menit. Sumber: Buku paket hal. 124130, 130132, 132134, 134136, 137141. Buku referensi lain. Alat: Laptop LCD OHP komplemen suatu kejadian. Peluang gabungan dua kejadian yang saling lepas. Peluang dua kejadian yang saling bebas. Memberikan tafsiran peluang komplemen suatu kejadian. Mendefinisik an dua kejadian yang saling lepas atau saling asing. Menentukan peluang gabungan dua kejadian yang saling lepas. Memberikan tafsiran peluang gabungan dua kejadian yang saling lepas. Peluang kejadian bersyarat. Mendefinisik an dua kejadian yang saling bebas. Menentukan peluang dua kejadian yang saling bebas. Memberikan tafsiran peluang dua kejadian yang saling bebas. Mendefinisik an peluang kejadian Menentukan peluang dua kejadian yang saling lepas dan penafsirannya. Menentukan peluang dua kejadian yang saling bebas dan penafsirannya. Menentukan peluang kejadian bersyarat. bersyarat. Percobaan, ruang sampel, dan kejadian. Peluang kejadian. Frekuensi harapan. Kejadian majemuk (komplemen suatu kejadian, peluang gabungan dua kejadian yang saling lepas, peluang dua kejadian yang saling bebas, peluang kejadian bersyarat). Menentukan peluang kejadian bersyarat. Memberikan tafsiran peluang gabungan dua kejadian bersyarat. Melakukan ulangan berisi materi yang berkaitan dengan percobaan, ruang sampel, dan kejadian, peluang kejadian, frekuensi harapan, kejadian majemuk (komplemen suatu kejadian, peluang gabungan dua kejadian yang saling lepas, peluang dua kejadian yang saling bebas, peluang kejadian bersyarat). Mengerjakan soal dengan baik berkaitan dengan materi mengenai percobaan, ruang sampel, dan kejadian, peluang kejadian, frekuensi harapan, kejadian majemuk (komplemen suatu kejadian, peluang gabungan dua kejadian yang saling lepas, peluang dua kejadian yang saling bebas, peluang kejadian bersyarat). Ulangan harian. Pilihan ganda. 1. Dari 5 orang akan dibagi menjadi 2 kelompok. Jika kelompok pertama terdiri atas 3 orang dan keompok kedua terdiri atas 2 orang, maka banyaknya cara mengelompokkan nya adalah..... a. 10 d. 100 Uraian singkat. b. 20 e. 400 c. 60 2. Kotak A berisi 5 bola merah dan 3 bola putih, sedangkan kotak B berisi 2 bola merah dan 6 bola putih. Dari dalam kotak masingmasing diambil sebuah bola secara acak. Peluang bahwa 2 x 45 menit. kedua bola yang terambil warnanya berlainan adalah….. Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : XI / IPA Semester : GANJIL STANDAR KOMPETENSI: 2.Menurunkan rumus trigonometri dan penggunaannya. Kompetensi Dasar 2.1. Menggunaka n rumus sinus dan kosinus jumlah dua sudut, selisih dua sudut, dan sudut ganda untuk menghitung sinus dan kosinus sudut tertentu. Materi Ajar Trigonometri. Rumus trigonometri jumlah dan selisih dua sudut: - Rumus kosinus jumlah dan selisih dua sudut. Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Berani mengambil resiko Disiplin Kerja keras Demokratis Keorisinilan Mengulang kembali mengenai konsep perbandingan sinus, cosinus, dan tangen. Menurunkan rumus kosinus jumlah dan selisih dua sudut. Menurunkan rumus sinus jumlah dan selisih dua sudut. Menggunakan rumus kosinus dan sinus jumlah dan - Rumus sinus jumlah dan selisih dua sudut. - Rumus tangen jumlah dan selisih dua Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Menggunakan rumus kosinus jumlah dan selisih dua sudut dalam pemecahan masalah. Menggunakan rumus sinus jumlah dan selisih dua sudut dalam pemecahan masalah. Menggunakan rumus tangen jumlah dan selisih dua sudut dalam Penilaian Teknik Bentuk Instrumen Tugas individu. Uraian singkat. Contoh Alokasi Waktu Instrumen (menit) 1. Diketahui A + B = 6 dan cos A cos B = 3 , 4 maka cos (A - B) = .... 2. Tentukan nilai dari sin 345o. 3. Tentukan nilai dari tan 195o. 4 x 45 menit. Sumber/Ba han /Alat Sumber: Buku paket (Buku Matema tika SMA dan MA ESIS Kelas XI Semeste r 1 Jilid 2A, karanga n Sri Kurnian ingsih,d kk) hal. 156158, 159160, sudut. selisih dua sudut untuk menyelesaikan soal. Rumus trigonometri sudut rangkap dan sudut tengahan: - Rumus sinus sudut rangkap (ganda). - Rumus kosinus sudut rangkap (ganda). - Rumus tangen sudut 160162, 162165. Menurunkan rumus tangen jumlah dan selisih dua sudut dari rumus kosinus dan sinus jumlah dan selisih dua sudut. Menggunakan rumus tangen jumlah dan selisih dua sudut untuk menyelesaikan soal. Menurunkan rumus tangen selisih dua sudut untuk menghitung besar sudut antara dua garis. Menurunkan rumus sinus sudut rangkap (ganda) dengan menggunakan rumus sinus jumlah dua sudut. pemecahan masalah. Menurunkan rumus kosinus sudut rangkap (ganda) dengan menggunakan rumus kosinus Buku referens i lain. Alat: Menggunakan rumus sinus, kosinus, dan tangen sudut rangkap (ganda). Kuis. Uraian singkat. 1. Diketahui tan A = P, maka sin 2A = .... 4 x 45 menit. Laptop LCD OHP Sumber: Buku paket hal. 165166, 166167, 168, 169173. rangkap (ganda). - Rumus trigonometri sudut tengahan. Rumus trigonometri jumlah dua sudut. Menurunkan rumus tangen sudut rangkap (ganda) dengan menggunakan rumus tangen jumlah dua sudut. Menggunakan rumus sinus, kosinus, dan tangen sudut rangkap (ganda) untuk menyelesaikan soal. Menurunkan rumus trigonometri untuk sudut tengahan dengan menggunakan rumus trigonometri sudut rangkap (ganda). Mengenal identitas sudut tengahan. Menggunakan rumus trigonometri sudut tengahan untuk menyelesaikan soal. Melakukan ulangan berisi Buku referens i lain. Alat: 2. Diketahui tan A Menggunakan rumus trigonometri (sinus, kosinus, dan tangen) sudut tengahan. Mengerjakan soal dengan baik = 1 , maka cos p 2A = .... Ulangan harian. Pilihan ganda. 1. Diketahui 2 x 45 menit. Laptop LCD OHP jumlah dan selisih dua sudut: materi yang berkaitan dengan rumus trigonometri (kosinus, sinus, dan tangen) jumlah dan selisih dua sudut, serta rumus trigonometri sudut rangkap (ganda) dan sudut tengahan. - Rumus kosinus jumlah dan selisih dua sudut. - Rumus sinus jumlah dan selisih dua sudut. - Rumus tangen jumlah dan selisih dua sudut. π π 2 cos A sin A 4 4 , maka….. berkaitan dengan materi mengenai rumus trigonometri (kosinus, sinus, dan tangen) jumlah dan selisih dua sudut, serta rumus trigonometri sudut rangkap (ganda) dan sudut tengahan. a. sin A = 12 b. tan A 3 c. tan A = 12 d. cos A = 1 2 3 e. sin A = 1 2 Uraian singkat. Rumus trigonometri sudut rangkap dan sudut tengahan: 2 2. Pada suatu segitiga PQR yang siku-siku di R, diketahui bahwa sin P sin Q = 2 dan 5 - Rumus sinus sudut rangkap (ganda). sin (P – Q) = 5p. Nilai p adalah …. - Rumus kosinus sudut rangkap (ganda). - Rumus tangen sudut rangkap (ganda). - Rumus trigonometri sudut tengahan. 2.2. Menurunkan rumus jumlah dan selisih sinus dan kosinus. Rumus perkalian, penjumlahan, dan pengurangan sinus dan Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Berani mengambil Menurunkan rumus perkalian kosinus dan kosinus dengan menggunakan rumus kosinus Menyatakan kosinus jumlah dan selisih dua sudut dalam perkalian kosinus dan kosinus Tugas individu. Uraian singkat. 1. Hitunglah 6 x 45 10 1 0menit. 3 cos 37 cos 7 2 2 . Sumber: Buku paket hal. 174, 175, kosinus: - Rumus perkalian kosinus dan kosinus. Disiplin Kerja keras resiko jumlah dan selisih dua sudut. Keorisinilan Demokratis - Rumus perkalian sinus dan sinus. - Rumus perkalian sinus dan kosinus. - Rumus penjumlahan dan pengurangan sinus, kosinus, dan tangen. Menurunkan rumus perkalian sinus dan sinus dengan cara mengurangkan rumus kosinus jumlah dua sudut dengan rumus kosinus selisih dua sudut. Menurunkan rumus perkalian sinus dan kosinus dengan cara menjumlahkan atau mengurangkan rumus sinus jumlah dan selisih dua sudut. Menurunkan rumus jumlah dan selisih kosinus. Menurunkan rumus jumlah dan selisih sinus. Menurunkan rumus jumlah dan selisih sinus dan kosinus menggunakan rumus perkalian sinus dan kosinus. Menyelesaikan masalah yang maupun perkalian sinus dan sinus. 176, 177178, 179. Menyatakan sinus jumlah dan selisih dua sudut dalam perkalian sinus dan kosinus. Menyatakan perkalian sinus dan kosinus dalam jumlah atau selisih sinus atau kosinus. Membuktikan rumus trigonometri jumlah dan selisih dari sinus dan kosinus dua sudut. Buku referens i lain. Alat: 2. Buktikan bahwa (cos 2 x cos 4 x cos 6 x) sin x sin 3x cos 4 x Laptop LCD OHP menggunakan rumus jumlah dan selisih kosinus, serta rumus jumlah dan selisih sinus. 2.3. Menggunaka n rumus jumlah dan selisih sinus dan kosinus. Rumus perkalian, penjumlahan, dan pengurangan sinus dan kosinus: Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Berani mengambil resiko - Rumus perkalian kosinus dan kosinus. Demokratis - Rumus perkalian sinus dan sinus. - Rumus perkalian Disiplin Kerja keras Keorisinilan Menurunkan rumus jumlah dan selisih tangen. Dengan memanipulasi rumus yang ada, menurunkan rumus baru. Membahas pembuktian soal yang melibatkan beberapa konsep trigonometri. Menggunakan rumus perkalian kosinus dan kosinus dalam pemecahan masalah. Menggunakan rumus perkalian sinus dan sinus dalam pemecahan masalah. Menggunakan rumus perkalian sinus dan kosinus dalam pemecahan Menyelesaikan masalah yang melibatkan rumus perkalian, penjumlahan, dan pengurangan sinus dan kosinus. Tugas Uraian kelompok. singkat. Buktikan bahwa sin 2 x 1 cos 2 x sin x cos x 4 x 45 menit. Sumber: Buku paket hal. 174175, 175176, 176177, 177181, 181183. Buku referens . sinus dan kosinus. masalah. - Rumus penjumlahan dan pengurangan sinus, kosinus, dan tangen. Identitas trigonometri. Rumus perkalian kosinus dan kosinus. Rumus perkalian sinus dan sinus. Rumus perkalian sinus i Menggunakan rumus jumlah dan selisih sinus, kosinus, dan tangen dalam pemecahan masalah. Menyimak pemahaman mengenai langkahlangkah pembuktian suatu identitas atau persamaan trigonometri. Membuktikan identitas trigonometri sederhana. Melakukan latihan menyelesaikan identitas trigonometri. Melakukan ulangan berisi materi yang berkaitan dengan rumus perkalian, penjumlahan, dan pengurangan sinus dan kosinus, lain. Alat: Merancang dan membuktikan identitas trigonometri. Mengerjakan soal dengan baik berkaitan dengan materi mengenai rumus perkalian, penjumlahan, dan pengurangan sinus dan kosinus, pembuktian rumus trigonometri jumlah dan selisih Ulangan harian. Uraian singkat. Nyatakan bentuk jumlah atau selisih sinus dan kosinus ke dalam bentuk perkalian sinus dan kosinus. a. sin 6x – sin 4x. b. cos (4x + y) – 2 x 45 menit. Laptop LCD OHP dan kosinus. Rumus penjumlahan dan pengurangan sinus, kosinus, dan tangen. Rumus perkalian kosinus dan kosinus. Rumus perkalian sinus dan sinus. Rumus perkalian sinus dan kosinus. Rumus penjumlahan dan pengurangan sinus, kosinus, dan tangen. Identitas trigonometri. pembuktian rumus trigonometri jumlah dan selisih dari sinus dan kosinus dua sudut, serta identitas trigonometri. dari sinus dan kosinus dua sudut, serta identitas trigonometri. cos (4x - y) SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : XI / IPA Semester : GANJIL STANDAR KOMPETENSI: 3. Menyusun persamaan lingkaran dan garis singgungnya. Kompetensi Dasar Materi Ajar Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Kegiatan Pembelajaran Ekonomi Kreatif Penilaian Indikator Pencapaian Kompetensi Teknik 3.1. Menyusun persamaan lingkaran yang memenuhi persyaratan yang ditentukan. Lingkaran. Persamaan lingkaran: - Persamaan lingkaran yang berpusat di O(0, 0). - Persamaan lingkaran yang berpusat di M(a, b) dan jari-jari r. - Bentuk umum persamaan Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Berani mengambil resiko Disiplin Kerja keras Demokratis Keorisinilan Menentukan persamaan lingkaran yang berpusat di O(0, 0) dengan jari-jari r menggunakan teorema Pyhtagoras. Menentukan posisi titik P(a, b) terhadap lingkaran yang berpusat di O(0, 0) dengan jari-jari r. Menentukan persamaan lingkaran yang berpusat di M(a, b) dengan jari-jari r. Merumuskan persamaan lingkaran yang berpusat di (0, 0) dan (a, b). Tugas Individu Bentuk Instrumen Uraian singkat. Alokasi Waktu (menit) Sumber /Bahan /Alat Contoh Instrumen 1. Persamaan lingkaran dengan pusat (2, -1) serta melalui titik (5, 2) adalah...... 4 x 45 menit. Sumber: Buku paket (Buku Matematika SMA dan MA ESIS Kelas XI Semester 1 Jilid 2A, karangan Sri Kurnianing sih, dkk) hal. 195198, 199-202, 202-206, 206-209. Buku referensi lingkaran. Kedudukan garis terhadap suatu lingkaran. lain. Menentukan posisi titik (c, d) terhadap lingkaran yang berpusat di (a, b) dengan jarijari r. Alat: Laptop LCD Menyatakan bentuk umum persamaan lingkaran. Mendefinisikan kuasa suatu titik terhadap lingkaran. Menentukan pusat dan jari-jari lingkaran yang diketahui persamaannya. Menyusun persamaan lingkaran yang memenuhi kriteria tertentu. Menentukan kedudukan garis terhadap suatu lingkaran. Menentukan syarat-syarat agar garis: 1. menyinggung lingkaran. 2. memotong lingkaran. 3. tidak memotong lingkaran (di OHP Menentukan pusat dan jari-jari lingkaran yang persamaannya diketahui. 2. Lingkaran yang melalui (2, 1), (6, 1), dan (2, 5) berjarijari....... Menentukan persamaan lingkaran yang memenuhi kriteria tertentu. Menentukan posisi garis terhadap lingkaran. 3. Agar garis y = mx tidak memotong lingkaran 2 2 x y 4 x 2 y 4 0 , berapakah nilai m ....... luar lingkaran). Persamaan lingkaran: persamaan lingkaran yang berpusat di O(0, 0), persamaan lingkaran yang berpusat di M(a, b) dan jari-jari r, bentuk umum persamaan lingkaran, kedudukan garis terhadap suatu lingkaran. 3.2. Menentukan Persamaan garis persamaan singgung: garis singgung Garis pada lingkaran singgung dalam pada berbagai lingkaran situasi. yang berpusat di O(0, 0). Garis singgung pada lingkaran yang berpusat di M(a, b) dan jari-jari r. Garis singgung Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Berani mengambil resiko Disiplin Kerja keras Demokratis Keorisinilan Melakukan ulangan berisi materi yang berkaitan dengan persamaan lingkaran (persamaan lingkaran yang berpusat di O(0, 0), persamaan lingkaran yang berpusat di M(a, b) dan jari-jari r, bentuk umum persamaan lingkaran, kedudukan garis terhadap suatu lingkaran). Mengerjakan soal dengan baik berkaitan dengan materi mengenai persamaan lingkaran (persamaan lingkaran yang berpusat di O(0, 0), persamaan lingkaran yang berpusat di M(a, b) dan jarijari r, bentuk umum persamaan lingkaran, kedudukan garis terhadap suatu lingkaran). Ulangan Pilihan harian. ganda. Menyelidiki sifat dari garis-garis yang menyinggung maupun tidak menyinggung lingkaran. Menentukan persamaan garis singgung yang melalui suatu titik pada lingkaran. Tugas Uraian kelompo obyektif. k. Menentukan rumus persamaan garis singgung yang melalui suatu titik pada lingkaran: Uraian obyektif. 1. Persamaan lingkaran yang berpusat di titik (-3, 2) dan menyinggung garis 3x4y 8 adalah....... 2. Titik pusat lingkaran 2 2 x y ax by 12 0 terletak pada garis 2x3y 0, di kuadran IV. Jika jarijari lingkaran adalah 1, nilai a dan b berturut-turut adalah...... 1. Diketahui persamaan garis singgung lingkaran (x3 )2y25, di titik yang berabsis 1 dan ordinat positif. Persamaan garis singgung yang tegak lurus garis singgung tersebut adalah..... 1. berpusat di O(0, 0). 4 x 45 menit. Sumber: Buku paket hal. 210211, 211214, 214217, 217220. Buku referensi lain. Alat: 2. berpusat di M(a, b) 3. persamaannya berbentuk umum. 2 x 45 menit. Menentukan persamaan garis singgung yang 2. Salah satu persamaan garis singgung lingkaran x2 y2 64dan titik Laptop LCD OHP pada lingkaran dengan gradien tertentu. Garis singgung dari suatu titik di luar lingkaran. Menentukan rumus persamaan garis singgung dengan gradien tertentu pada: 1. lingkaran berpusat di O(0, 0). 2. lingkaran berpusat di M(a, b) gradiennya diketahui. (-10, 0) adalah..... Menggunakan diskriminan atau dengan cara lain untuk menentukan persamaan garis singgung dari suatu titik di luar lingkaran. Menyelesaikan soal mengenai persamaan garis singgung dari suatu titik di luar lingkaran dengan menggunakan diskriminan dan dengan cara lain. Persamaan garis singgung: garis singgung pada lingkaran yang berpusat di O(0, 0), garis singgung pada lingkaran yang berpusat di M(a, b) dan jari-jari r, garis singgung pada lingkaran dengan gradien tertentu, garis singgung dari suatu titik di luar lingkaran. Melakukan ulangan berisi materi yang berkaitan dengan persamaan garis singgung (garis singgung pada lingkaran yang berpusat di O(0, 0), garis singgung pada lingkaran yang berpusat di M(a, b) dan jari-jari r, garis singgung pada lingkaran dengan gradien tertentu, garis singgung dari suatu titik di luar lingkaran). Mengerjakan soal dengan baik berkaitan dengan materi mengenai persamaan garis singgung (garis singgung pada lingkaran yang berpusat di O(0, 0), garis singgung pada lingkaran yang berpusat di M(a, b) dan jarijari r, garis singgung pada lingkaran dengan gradien tertentu, garis singgung dari suatu titik di Ulangan Pilihan harian. ganda. Uraian singkat. 1. Dari titik T(10, 9) 2 x 45 dibuat garis singgung menit. yang menyinggung lingkaran 2 2 x y 4 x 6 y 23 di titik S. Panjang TS = ...... a. 4 10 d. b. 6 12 e. c. 8 2. Salah satu persamaan garis singgung lingkaran 2 2 x y 4 x 6 y 68 0 yang tegak lurus luar lingkaran). garis AB dengan A(-2, 3) dan B(-5, 7) adalah...... Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran : Matematika Satuan Pendidikan : SMA / MA Kelas/Semester : XI/2 Nama Guru NIP/NIK Sekolah : ........................... : ........................... : ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : XI / IPA Semester : GENAP STANDAR KOMPETENSI: 4. Menggunakan aturan sukubanyak dalam penyelesaian masalah. Kompetensi Dasar 4.1. Menggunakan algoritma pembagian sukubanyak untuk menentukan hasil bagi dan sisa pembagian Materi Ajar Sukubanyak Pengertian sukubanyak: - Derajat dan koefisien koefisien sukuban yak. - Pengidenti fikasi an sukubanya k - Penentuan nilai sukubanya Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Percaya diri Keorisinilan Memahami pengertian sukubanyak dengan menyebutkan derajat sukubanyak dan koefisienkoefisien tiap sukunya. Mengidentifika si bentuk matematika yang merupakan sukubanyak. Menentukan nilai dari suatu sukubanyak dengan Menentukan derajat dan koefisienkoefisien tiap suku dari sukubanyak serta mengidentifikasi bentuk matematika yang merupakan sukubanyak. Menentukan nilai dari suatu sukubanyak dengan menggunakan cara substitusi Penilaian Teknik Tugas individu. Bentuk Instrumen Uraian singkat. Contoh Instrumen 1. Tentukan derajat beserta koefisienkoefisien dan kontanta dari sukubanyak berikut: Alokasi Waktu Sumber/ Bahan / (menit) Alat 2 45 menit. Sumber: Buku paket (Buku Matemati ka SMA dan MA ESIS Kelas XI Semester 2 Jilid 2B, karangan Sri Kurniani ngsih,dk k) hal. 25, 6-11. Buku referensi a. 2x3 8x2 3x 5 b. 6 y4 8 y3 3 y 84 c. 2t 2 8t 4 3t3 10t 5 2. Tentukan bentuk matematika berikut merupakan sukubanyak atau bukan: k. menggunakan cara substitusi atau skema. langsung dan skema. lain. a. 2x4 8x2 3x 50 . b. x3 Alat: 1 3 2x 1 x x2 . Operasi antar sukubanyak: - Penjumlah an sukubanya k. - Pengurang an sukubanya k. - Perkalian sukubanya k. - Kesamaan sukubanya k. Menyelesaikan operasi antar sukubanyak yang meliputi penjumlahan, pengurangan, dan perkalian sukubanyak serta menentukan derajatnya. Memahami pengertian dari kesamaan sukubanyak untuk menentukan koefisien dari sukubanyak yang sama. Menyelesaikan operasi antar sukubanyak yang meliputi penjumlahan, pengurangan, dan perkalian sukubanyak. Tugas individu. Uraian singkat. 1. Diketahui sukubanyak f x x3 8 x 2 4 x 5 2 45 menit. Laptop LCD OHP Sumber: Buku paket hal. 11-14 Buku referensi lain. dan g x 28 x 2 9 x 40 , tentukan: a. f x g x dan derajatnya. Menentukan koefisien yang belum diketahui nilainya dari dua sukubanyak yang sama. b. f x g x dan derajatnya. c. f x g x dan derajatnya. 2. Tentukan nilai p dari kesamaan sukubanyak berikut. ( x 1)2 ( x 2)( x 3) 2 p Alat: Laptop LCD OHP Pembagian sukubanyak: Bentuk panjang. Sintetik Horner (bentuk linear dan bentuk kuadrat). 4.2. Menggunakan teorema sisa dan teorema faktor dalam pemecahan masalah. Teorema sisa: Rasa ingin tahu - Pembagia n dengan Mandiri x k . Kreatif - Pembagia n dengan ax b . Kerja keras - Pembagi an dengan x a x b - Pembagi an dengan Berorientasi tugas dan hasil Percaya diri Keorisinilan Menentukan hasil bagi dan sisa pembagian dari pembagian sukubanyak oleh bentuk linear atau kuadrat menggunakan cara pembagian bentuk panjang dan sintetik Horner. Menentukan derajat hasil bagi dan sisa pembagian sukubanyak. Menentukan hasil bagi dan sisa pembagian dari pembagian sukubanyak oleh x k dengan menggunakan teorema sisa. Menentukan hasil bagi dan sisa pembagian dari pembagian sukubanyak oleh ax b dengan menggunakan teorema sisa. Menentukan hasil bagi dan sisa pembagian dari pembagian sukubanyak oleh bentuk linear atau kuadrat serta menentukan derajat hasil bagi dan sisa pembagiannya dengan menggunakan cara pembagian sukubanyak bentuk panjang dan sintetik (Horner). Tugas individu. Uraian singkat. Tentukan hasil bagi dan sisa pembagian serta derajatnya pada pembagian sukubanyak berikut dan nyatakan hasilnya dalam bentuk persamaan dasar pembagian: a. b. c. 2 45 menit. 2x3 8x2 3x 5 dibagi oleh x 1 . Sumber: Buku paket hal. 15-25 Buku referensi lain. Alat: 6 y 4 8 y3 3 y 84 dibagi oleh 2 y 3 . Laptop LCD OHP 2t 2 8t 4 3t3 10t 5 dibagi oleh t 2 2t 6 . Menentukan hasil bagi dan sisa pembagian dari pembagian sukubanyak oleh bentuk linear dan kuadrat dengan menggunakan teorema sisa. Tugas individu. . Uraian singkat. Tentukan hasil bagi dan sisa pembagian berikut beserta derajatnya: o x3 8x2 30x 5 dibagi oleh x 5 o 2x4 20x3 8x2 3x 5 dibagi oleh x2 2 x 6 o x4 2x3 8x2 x 4 di bagi oleh x 4 2x 1 2 45 menit. Sumber: Buku paket hal. 2634. Buku referensi lain. Alat: Laptop LCD OHP x k ax b Teorema faktor - Persama Menentukan hasil bagi dan sisa pembagian dari pembagian sukubanyak oleh x a x b dengan menggunakan teorema sisa. Menentukan hasil bagi dan sisa pembagian dari pembagian sukubanyak oleh x a x b dengan menggunakan teorema sisa. Menentukan hasil bagi dan sisa pembagian dari pembagian sukubanyak oleh x k ax b dengan menggunakan teorema sisa. Membuktikan teorema sisa. Menentukan faktor linear dari sukubanyak Membuktikan teorema sisa. Menentukan faktor linear dari sukubanyak dengan Tugas individu. Uraian singkat. 1. Faktorkanlah sukubanyak 2x3 3x2 17 x 12 2 45 menit. Sumber: Buku paket an sukuban yak dengan menggunakan teorema faktor. - Akarakar rasional persama an sukuban yak: Menentukan akarakar rasional suatu persamaan sukubanya k Menentu kan akarakar mendekati akar nyata persamaan sukubanya k Pengertian sukubanyak Operasi antar sukubanyak Teorema sisa Teorema faktor Persamaan menggunakan teorema faktor. . hal. 3450. Menunjukkan faktor linear dari suatu sukubanyak dengan menggunakan teorema faktor. Membuktikan teorema faktor. Menentukan akar-akar rasional suatu persamaan sukubanyak dengan menggunakan teorema faktor. Menentukan akar-akar mendekati akar nyata persamaan sukubanyak dengan menggunakan perhitungan dan grafik. Melakukan ulangan berisi materi yang berkaitan dengan pengertian sukubanyak, menentukan nilai sukubanyak, operasi antar Buku referensi lain. Alat: Membuktikan teorema faktor. Menentukan akar-akar suatu persamaan sukubanyak. Mengerjakan soal dengan baik berkaitan dengan materi mengenai pengertian sukubanyak, menentukan nilai sukubanyak, operasi antar 2. Tentukan akar-akar rasional dari persamaan berikut. 2x4 5x3 17 x2 41x 21 0 Ulangan Harian. Uraian singkat. 1. Tentukan hasil dan sisa pembagian dari pembagian x3 3x2 5x 10 oleh x 3 . 2. Tentukan apakah bentuk matematika berikut merupakan 2 45 menit. Laptop LCD OHP sukubanyak sukubanyak, cara menentukan hasil bagi dan sisa pembagian dari pembagian sukubanyak oleh bentuk linear dan kuadrat dengan menggunakan teorema sisa, dan cara menyelesaikan suatu persamaan sukubanyak dengan menentukan faktor linear nya menggunakan teorema faktor. sukubanyak, cara menentukan hasil bagi dan sisa pembagian dari pembagian sukubanyak oleh bentuk linear dan kuadrat dengan menggunakan teorema sisa, dan cara menyelesaikan suatu persamaan sukubanyak dengan menentukan faktor linear nya menggunakan teorema faktor. sukubanyak atau bukan. a. 5x x3 2 x2 b. 5 x x3 2 x2 3 x 3. Diketahui x 2 adalah faktor dari sukubanyak Pilihan P x 2 x3 ax 2 7 x 6 Ganda. . Salah satu faktor lainnya adalah .... a. x 3 d. 2 x 3 b. 2 x 3 e. x 1 c. x 3 Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : XI / IPA Semester : GENAP STANDAR KOMPETENSI: 5. Menentukan komposisi dua fungsi dan invers suatu fungsi. Kompetensi Dasar 5.1. Menentukan komposisi fungsi dari dua fungsi. Materi Ajar Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Komposisi fungsi dan fungsi invers. Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Sifat khusus yang mungkin dimiliki oleh fungsi: - Fungsi satusatu (Injektif). Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Kerja keras - Fungsi pada (Surjektif). - Fungsi satusatu pada (Bijektif). - Kesamaan dua fungsi Mengingat kembali materi kelas X mengenai pengertian fungsi dan jenis-jenis fungsi khusus. Memahami sifat khusus yang mungkin dimiliki oleh sebuah fungsi yaitu fungsi satu-satu, pada, serta satu-satu dan pada. Memahami sifat kesamaan Menentukan sifat khusus yang mungkin dimiliki oleh sebuah fungsi. Penilaian Teknik Bentuk Instrumen Tugas Uraian individu. singkat. Contoh Alokasi Waktu Instrumen (menit) 4. Apakah fungsi berikut merupakan fungsi bijektif? 2 45 menit. Sumber/Bahan /Alat Sumber: Buku paket (Buku Matematika SMA dan MA ESIS Kelas XI Semester 2 Jilid 2B, karangan Sri Kurnianings ih,dkk) hal. 62-75. Buku referensi lain. a. f : x 2x 3 b. f : x 2 x2 5 Alat: dari dua fungsi. Aljabar fungsi Memahami operasioperasi yang diterapkan pada fungsi. Laptop LCD OHP 5. Diketahui f x x 2 dan Melakukan operasi-operasi aljabar yang diterapkan pada fungsi. 2 . 3x 6 Tentukan rumus fungsi berikut dan tentukan pula daerah asalnya (D). g x Menentukan daerah asal dari fungsi hasil operasi yang diterapkan. a. f g x b. f g x c. f g x f d. x g Komposisi fungsi: - Pengertian komposisi fungsi. - Komposisi fungsi pada sistem bilangan real. - Sifat-sifat dari komposisi fungsi. Memahami pengertian komposisi fungsi Menentukan rumus fungsi dari setiap fungsi yang diberikan. Menjelaskan komposisi fungsi pada sistem bilangan real yang meliputi nilai fungsi komposisi terhadap komponen pembentuknya Menentukan rumus fungsi dari setiap fungsi yang diberikan. Tugas Uraian individu. singkat. 1. Diketahui f : dengan 2 45 menit. Sumber: Buku paket hal. 75-81. Buku referensi lain. f x 2x 2 dan g : dengan g x x 1 . 2 Tentukanlah: a. f g x , Alat: b. g f x , Laptop g x 1 LCD OHP c. Menentukan komponen f 2. Tentukan rumus Menentukan komponen pembentuk fungsi komposisi bila aturan komposisi dan komponen lainnya diketahui. Menjelaskan sifat-sifat dari komposisi fungsi. pembentuk fungsi komposisi bila aturan komposisi dan komponen lainnya diketahui. fungsi g(x) jika diketahui f(x) = x + 2 dan (fog)(x) = 3x – 5. Komposisi fungsi dan fungsi invers. Sifat khusus yang mungkin dimiliki oleh fungsi Aljabar fungsi Komposisi fungsi Melakukan ulangan harian berisi materi yang berkaitan dengan sifat khusus yang mungkin dimiliki oleh sebuah fungsi, operasioperasi yang diterapkan pada fungsi, daerah asal dari fungsi hasil operasi yang diterapkan, menjelaskan nilai fungsi komposisi terhadap komponen pembentuknya , menentukan komponen pembentuk fungsi komposisi bila aturan komposisi dan Mengerjakan soal dengan baik berkaitan dengan sifat khusus yang mungkin dimiliki oleh sebuah fungsi, operasioperasi yang diterapkan pada fungsi, daerah asal dari fungsi hasil operasi yang diterapkan, menjelaskan nilai fungsi komposisi terhadap komponen pembentuknya, menentukan komponen pembentuk fungsi komposisi bila aturan komposisi dan komponen lainnya diketahui, dan menyebutkan sifat-sifat dari komposisi Ulangan Pilihan Diketahui g : Harian Ganda. ditentukan oleh fungsi g x x2 x 2 dan f : sehingga f g x 2x2 2x 5 , maka f x sama dengan .... a. 2 x 3 d. 2 x 3 b. 2x 1 e. 2 x 9 c. 2x 1 2 45 menit. komponen lainnya diketahui, dan menyebutkan sifat-sifat dari komposisi fungsi. 5.2. Menentukan invers suatu fungsi. Fungsi Invers: - Pengertian invers fungsi. Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras - Menentukan rumus fungsi invers. Grafik suatu fungsi dan grafik fungsi inversnya. Memahami pengertian dari invers suatu fungsi. Menentukan rumus fungsi invers dari suatu fungsi. Tugas Uraian individu. singkat. Menjelaskan syarat suatu fungsi mempunyai invers. Menentukan rumus fungsi invers dari fungsi yang diketahui dan sebaliknya. Menggambark an grafik fungsi invers dari grafik fungsi asalnya. Menentukan daerah asal fungsi inversnya. Tentukan invers dari fungsi atau relasi berikut kemudian gambarkan diagram panah fungsi atau relasi tersebut beserta diagram panah inversnya: a. Menentukan apakah suatu fungsi mempunyai invers atau tidak. fungsi. b. Menggambarkan grafik fungsi invers dari grafik fungsi asalnya. Tugas Uraian individu. singkat. 3, 2 ; 2, 0 ; 1, 2 45 menit. 2 Sumber: Buku paket hal. 81-86. Buku referensi lain. Alat: 0, 4 ; 1, 6 ; 2, 8 Laptop 3, a ; 2, b ; 1, c ; 0, d LCD OHP Diketahui fungsi f x 2 x3 3 . Tentukan: 2 45 menit. Sumber: hal. 86-88. Buku referensi lain. a. rumus fungsi f 1 x , b. daerah asal fungsi f x dan Alat: Laptop f 1 x , c. gambarlah grafik fungsi f x dan LCD OHP f 1 x . Fungsi invers dari fungsi komposisi Fungsi Invers: Fungsi invers dari fungsi komposisi. Membahas teorema yang berkenaan dengan fungsi invers. Menentukan fungsi invers dari fungsi komposisi dan nilainya. Tugas Uraian individu. singkat. Diketahui 3x 2 dan f ( x) 4x 3 g ( x) 2 x 1 . Tentukan 2 45 menit. Menentukan rumus fungsi invers dari fungsi kompisisi. Menentukan nilai fungsi kompisisi dan fungsi invers dari fungsi komposisi tersebut. Melakukan ulangan harian berisi materi yang berkaitan dengan pengertian invers fungsi, menentukan hal. 88-93. Buku referensi lain. ( f g )1(3). Menentukan rumus komposisi fungsi dari dua fungsi yang diberikan. Sumber: Alat: Mengerjakan soal dengan baik berkaitan dengan pengertian invers fungsi, menentukan rumus fungsi invers, Ulangan harian Pilihan ganda. 1. Diketahui f x 5 6x dan g x 3x 12 , maka f 1 g x .... 2 45 menit. Laptop LCD OHP rumus fungsi invers, menggambark an grafik fungsi invers, dan teorema yang berkenaan dengan fungsi invers. menggambarkan grafik fungsi invers, dan teorema yang berkenaan dengan fungsi invers. a. 18x 27 d. 2x 19 d. b. 18x 67 e. 1 x4 3 e. c. 2x 29 Uraian singkat. 2. Diketahui f x 3 3 x3 dan g x 3x 1 . Tentukanlah: a. f 1 x dan g 1 x , b. d. f g 1 x dan g f 1 2 , c. Grafik fungsi f x , f 1 x , g x , g 1 x , dan g 1 f 1 x e. Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. SILABUS PEMBELAJARAN Nama Sekolah : ................................... Mata Pelajaran : MATEMATIKA Kelas / Program : XI / IPA Semester : GENAP STANDAR KOMPETENSI: 6. Menggunakan konsep limit fungsi dan turunan fungsi dalam pemecahan masalah. Kompetensi Dasar 6.1. Menjelaskan secara intuitif arti limit fungsi di suatu titik dan di takhingga dan menggunakan sifat limit fungsi untuk menghitung bentuk tak tentu fungsi aljabar dan trigonometri. Materi Ajar Limit fungsi Limit fungsi aljabar: - Definisi limit secara intiutif. Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras - Definisi limit secara aljabar. - Limit fungsifungsi Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Menjelaskan arti limit fungsi secara intiutif berdasarkan fungsi aljabar yang sederhana. Menjelaskan arti limit fungsi secara aljabar berdasarkan fungsi aljabar sederhana. Menghitung limit fungsi aljabar di suatu titik menggunakan Menghitung limit fungsi aljabar di suatu titik dan tak hingga. Penilaian Teknik Bentuk Instrumen Tugas individu Uraian singkat. Alokasi Waktu Contoh Sumber/Bahan /Alat (menit) Instrumen Tentukan limit fungsi-fungsi berikut ini: a. lim 2 x 2 3 x 1 b. lim 4 45 menit. Sumber: x 2 3x 4 x 1 x 1 c. lim x x2 4 Buku paket (Buku Matematika SMA dan MA ESIS Kelas XI Semester 2 Jilid 2B, karangan Sri Kurnianingsih ,dkk) hal. 104-118. x Buku referensi lain. berbentu k lim f x cara substitusi, faktorisasi, dan perkalian dengan sekawan. x c (cara substitusi , faktorisa si, dan perkalian sekawan) . Menghitung limit fungsi aljabar di tak hingga . Memahami teorema-teorema limit dalam perhitungan limit fungsi. Alat: Laptop LCD OHP - Limit fungsi di tak hingga Teoremateorema limit : - Mengguna kan teorema limit untuk menghitun g limit fungsi aljabar dan trigonomet ri. - Mengguna kan teorema limit untuk menghitun g bentuk tak tentu limit fungsi. Menjelaskan teorema-teorema limit yang digunakan dalam perhitungan limit. Menggunakan teorema limit dalam menghitung bentuk tak tentu fungsi aljabar. Menggunakan sifat limit fungsi untuk menghitung bentuk tak tentu fungsi aljabar. Tugas individu. Uraian singkat. Tentukan limit fungsi-fungsi berikut ini: a. lim 2 x 2 3 x 1 x 3 b. lim x 2 3x 4 x 1 x 1 c. lim x x3 x6 2 45 menit. Sumber: Buku paket hal. 118-124. Buku referensi lain. Alat: Laptop LCD OHP Limit fungsi trigonometri : Memahami teorema limit apit. - Teorema limit apit. Menggunakan teorema limit apit dalam menentukan nilai sin x dan lim x 0 x - Menentuka n nilai lim x 0 sin x . x lim x x 0 sin x Tugas Menghitung limit fungsi trigonometri individu. di suatu titik. Uraian singkat. Hitunglah nilai cos 2 x . 1 sin x 4 2 45 menit. Sumber: Buku paket hal. 124-130. Buku referensi lain. lim x Alat: . - Menentuka n nilai x . x 0 sin x Laptop LCD OHP lim Penggunaan limit Kekontinua n dan diskontinua n (pengayaan) . Menjelaskan penggunaan limit dalam mencari garis singgung suatu kurva di suatu titik tertentu. Menggunakan limit dalam mencari garis singgung suatu kurva dan laju perubahan suatu fungsi. Menggunakan limit dalam menentukan laju perubahan suatu fungsi pertumbuhan. Memahami kekontinuan dan diskontinuan dari suatu fungsi. Menunjukkan kekontinuan suatu fungsi. Menghapus diskontinuan Tugas individu. Uraian singkat. 1. Gambarkan garis singgung kurva f x x2 4x 3 di x 1, 0, 2 45 menit. Sumber: Buku paket hal. 130-134, hal 135-138. Buku referensi lain. 1 . 2 Alat: Menyelidiki kekontinuan suatu fungsi. 2. Selidiki kekontinuan fungsi-fungsi berikut: x2 4 x2 x=2 f. f x di g. f x x2 6 Laptop LCD OHP suatu fungsi. Limit fungsi aljabar Teoremateorema limit Limit fungsi trigonometri Penggunaan limit Melakukan ulangan harian berisi materi yang berkaitan dengan cara menghitung limit fungsi aljabar di suatu titik dan tak hingga serta menggunakan teoremateorema limit dalam menghitung limit fungsi aljabar dan trigonometri dan bentuk tak tentu limit fungsi, serta menggunakan limit dalam mencari garis singgung suatu kurva dan laju perubahan suatu fungsi. di Mengerjakan soal dengan baik berkaitan dengan materi mengenai cara menghitung limit fungsi aljabar di suatu titik dan tak hingga serta menggunakan teorema-teorema limit dalam menghitung limit fungsi aljabar dan trigonometri dan bentuk tak tentu limit fungsi, serta menggunakan limit dalam mencari garis singgung suatu kurva dan laju perubahan suatu fungsi. Ulangan harian. Pilihan ganda. x=0 2 45 2 1 menit. lim x 1 x 2 1 x 1 Nilai sama dengan .... 3 4 a. d. 3 4 b. 1 2 e. 1 c. 1 2 6.2. Menggunakan konsep dan aturan turunan dalam perhitungan turunan fungsi. Turunan fungsi: - Definisi turunan fungsi. - Notasi turunan. Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Memahami definisi turunan fungsi. Menghitung turunan fungsi dengan menggunakan definisi turunan. Menjelaskan arti fisis dan geometri turunan fungsi di suatu titik. Menentukan turunan suatu fungsi di satu titik tertentu.. Menjelaskan dan menentukan laju perubahan nilai fungsi. Memahami notasi turunan fungsi. Menggunakan notasi turunan dalam menentukan laju perubahan nilai fungsi. Menghitung turunan fungsi dengan menggunakan definisi turunan. Tugas Uraian kelompok. singkat. 3. Tentukan turunan pertama fungsi berikut dengan menggunakan definisi turunan. 2 45 menit. Sumber: Buku paket hal. 148-155. Buku referensi lain. a. f x x 4 x 3 2 b. f x x3 3 Menentukan turunan suatu fungsi di satu titik tertentu. 4. Jika f x 4x 3 , carilah f ' 2 , f ' 1 , f ' 0 5. Misalkan Menentukan laju perubahan nilai fungsi terhadap variabel bebasnya y 4z2 1 , tentukan dy . dz Alat: Laptop LCD OHP Teoremateorema umum turunan fungsi. Turunan fungsi trigonometr i. o Turunan fungsi komposisi dengan aturan rantai. Menjelaskan teoremateorema umum turunan fungsi. Menentukan turunan fungsi aljabar dan trigonometri. Tugas individu. Uraian singkat. Tentukan turunan fungsi 2 45 menit. a. 20x4 3x2 5x b. c. Memahami mengenai teorema aturan rantai. Menggunakan aturan rantai dalam menentukan turunan suatu fungsi. Buku paket hal. 155-167. Buku referensi lain. 20 x3 3 x 2 3x 4 Alat: sin 2x 1 cos3x Membuktikan teoremateorema umum turunan fungsi. Menentukan turunan fungsi komposisi dengan aturan rantai. fungsi berikut: Menggunakan teoremateorema turunan fungsi untuk menghitung turunan fungsi aljabar dan trigonometri. Mengingat kembali aturan dari komposisi fungsi. Sumber: Tentukan Tugas individu. Uraian singkat. dy jika dx fungsinya adalah: a. y 4u14 1 dan Laptop LCD OHP 2 45 Sumber: menit Buku paket hal. 167-171. Buku referensi lain. u 2x 3 1 b. y 10u 2 dan u x2 2 x 1 Alat: Laptop LCD OHP Persamaan garis singgung di suatu titik pada kurva. Mengingat kembali materi mengenai arti fisis dan geometri dari turunan fungsi di suatu titik. Menentukan persamaan garis singgung pada suatu kurva. Tugas individu. Uraian singkat. Carilah persamaan garis Teoremateorema umum turunan fungsi. Turunan fungsi trigonometr i. Turunan fungsi komposisi dengan aturan rantai. Persamaan garis singgung di suatu titik menit Buku paket hal. 172-175. Buku referensi lain. berikut: 2 a. y 3x 5 x di 0, 1 b. y Alat: x2 5 di 2x 3 0, 1 Membahas cara menentukan persamaan garis singgung pada suatu kurva di suatu titik. Melakukan ulangan harian berisi materi yang berkaitan dengan cara menghitung turunan fungsi dengan menggunakan definisi turunan, menggunakan teoremateorema umum turunan untuk menghitung limit fungsi aljabar dan trigonometri di suatu titik dan tak hingga, cara menghitung turunan fungsi komposisi dengan aturan Sumber: singgung pada kurva Menentukan gradien dari suatu kurva di suatu titik. Turunan fungsi: 2 45 Mengerjakan soal dengan baik yang berkaitan dengan cara menghitung turunan fungsi dengan menggunakan definisi turunan, menggunakan teorema-teorema umum turunan untuk menghitung limit fungsi aljabar dan trigonometri di suatu titik dan tak hingga, cara menghitung turunan fungsi komposisi dengan aturan rantai, dan menentukan persamaan garis singgung pada Ulangan harian. Pilihan ganda. Jika f x x2 3 2x 1 dan 2 45 menit f ' x adalah turunan pertama f x , maka f ' 2 adalah .... a. 1 9 d. 2 9 b. 4 9 e. 2 c. 2 9 Laptop LCD OHP pada kurva. 6.3. Menggunakan turunan untuk menentukan karakteristik suatu fungsi dan memecahkan masalah. Fungsi naik dan fungsi turun rantai, dan menentukan persamaan garis singgung pada kurva di suatu titik. Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Memahami definisi fungsi naik dan fungsi turun. kurva di suatu titik. Uraian Menentukan selang Tugas dimana fungsi naik kelompok. singkat. atau turun. Menentukan selang interval dimana fungsi naik dan turun. Tentukan interval agar 2 45 menit. fungsi-fungsi berikut naik - Mensket sa grafik dengan uji turunan pertama. - Mensket sa grafik dengan uji turunan kedua. Mensketsa grafik dengan uji turunan pertama dengan menentukan titik stasionernya. Mensketsa grafik dengan uji turunan kedua dan menentukan jenis titik ekstrimnya. Buku paket hal. 175-180. Buku referensi lain. a. 20x4 3x2 5x x3 8 x2 Alat: c. x x 2 1 Sketsa grafik dengan uji turunan. atau turun: b. Sumber: Menentukan titik stasioner suatu fungsi beserta jenis ekstrimnya. Mensketsa grafik fungsinya. Tugas individ u. Uraian singkat. Misalkan 3 2 y x 2 x 3x 4 : a. Tentukan 4 45 menit. Laptop LCD OHP Sumber: Buku paket hal. 180-192 Buku referensi lain. dy d2y dan dx dx2 , b. Tentukan semua titik Alat: Laptop stasionernya dan LCD tentukan jenisnya, OHP c. Buat sketsa grafiknya. Pergerakan. - Kecepata n. - Percepat an. Memahami pengertian dari kecepatan dan percepatan. Menghitung kecepatan dan dan percepatan dengan menggunakan turunan. Menggunakan turunan dalam perhitungan kecepatan dan percepatan. Tugas individ u. Uraian singkat. Posisi benda sepanjang 2 45 lintasan (s) setelah t menit. detik dinyatakan dengan s(t). Dimana Sumber: Buku paket hal. 193-196. s t 2t 2 3t 4 . Buku referensi lain. Tentukan: a. v t dan a t b. v 2 dan a 2 Alat: c. t dimana a t 0 Penggunaan turunan dalam bentuk tak tentu. - Bentuk tak tentu 0 0 . - Bentuk tak tentu lainnya. Mengingat kembali materi mengenai cara menghitung limit fungsi di sutu titik dan bentuk tak tentu limit fungsi. Fungsi naik dan fungsi turun Menentukan limit fungsi bentuk tak tentu. Tugas individ u. Uraian singkat. Tentukan lim x2 5x 4 2 45 menit. 0 0 Menggunakan turunan dalam menghitung limit bentuk tak tentu lainnya. Melakukan ulangan harian berisi materi LCD OHP Sumber: Buku paket hal. 197-203. Buku referensi lain. Alat: . Laptop x 5 x 2 4 x 5 Menggunakan turunan. dalam menghitung limit bentuk tak tentu Mengerjakan soal dengan baik yang berisi materi yang Ulanga n harian. Uraian singkat. 1. Tentukan limit berikut : 2 45 menit. Laptop LCD OHP yang berkaitan dengan cara menentukan selang dimana fungsi naik atau turun, menentukan titik stasioner dan jenisnya, mensketsa grafiknya, dan cara penggunaan turunan dalam menghitung kecapatan, percepatan, limit fungsi bentuk tak tentu Sketsa grafik dengan uji turunan. Pergerakan. Penggunaan turunan dalam bentuk tak tentu. berkaitan dengan cara menentukan selang dimana fungsi naik atau turun, menentukan titik stasioner dan jenisnya, mensketsa grafiknya, dan cara penggunaan turunan dalam menghitung kecapatan, percepatan, limit fungsi bentuk tak x3 8 x 2 x 2 a. lim b. lim x3 4 x 3 x x3 14 x Pilihan ganda. 2. Jarak yang ditempuh sebuah mobil dalam waktu t diberikan oleh fungsi 1 f t t 3 3t 2 5t 3 . tentu 0 dan 0 lainnya . Kecepatan tertinggi mobil 0 dan lainnya . 0 itu dicapai pada waktu t adalah adalah .... a. 5 d. 2 b. 4 e. 1 c. 3 6.4. Menyelesaikan model matematika dari masalah yang berkaitan dengan ekstrim fungsi dan penafsirannya. Masalah maksimum dan minimum. - Masalah maksimu m dan minimu m jika fungsiny a diketahui . Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Mengingat kembali materi mengenai cara menghitung turunan fungsi. Menyelesaikan masalah maksimum dan minimum jika fungsinya diketahui. Menafsirkan solusi dari Menentukan penyelesaian dari model matematika yang berkaitan masalah maksimum dan minimum. Tugas individ u. Uraian singkat. 1. Keuntungan (K) per barang yang diperoleh sebuah toko dengan menjual x barang dengan tipe tertentu adalah 4 45 menit Sumber: Buku paket hal. 203-211. Buku referensi lain. K 40 x 25x3 200 2x Tentukan: a. banyak barang yang harus Alat: Laptop LCD - Masalah maksimu m dan minimu m jika fungsiny a tidak diketahui . masalah yang diperoleh. dijual untuk memaksimum kan keuntungan, b. keuntungan maksimum per barang, c. keuntungan total per hari dengan menjual sejumlah tersebut. 2. Jumlah dua angka adalah 40 dan hasil kali kedua bilangan tersebut maksimum tentukanlah kedua bilangan tersebut. 6.5. Merancang dan menyelesaikan model matematika dari masalah yang berkaitan dengan ekstrim fungsi. Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Menjelaskan karakteristik masalah dimana fungsinya tidak diketahui yang akan dicari maksimum atau minimumnya. Menentukan besaran masalah yang akan dijadikan sebagai variabel dalam ekspresi matematikanya. Merumuskan fungsi satu variabel yang merupakan model matematika dari Kerja keras OHP masalah. Masalah maksimum dan minimum. Menentukan penyelesaian dari model matematika tersebut. Memberikan tafsiran terhadap solusi dari masalah dimana fungsinya tidak diketahui. Melakukan ulangan harian berisi materi yang berkaitan dengan cara menyelesaikan masalah maksimum dan minimum jika fungsinya diketahui dan tidak diketahui. Mengerjakan soal dengan baik yang berisi materi berkaitan dengan cara menyelesaikan masalah maksimum dan minimum jika fungsinya diketahui dan tidak diketahui. Ulanga n harian. Pilihan ganda. 1. Jumlah biaya untuk memproduksi tas sejumlah p setiap harinya adalah 1 Rp p2 35 p 25 ribu 4 dan harga setiap tas 1 Rp 50 p ribu 2 supaya keuntungannya optimal,maka banyaknya tas yang harus diproduksi setiap harinya adalah .... a. 20 d. 10 b. 18 e. 5 c. 15 2. Suatu perusahaan mempunyai p karyawan. Total 2 45 menit. gaji seluruh karyawan tersbut adalah Uraian singkat. p 15.000 2 p2 . Tentukan banyak karyawan sehingga total gajinya mencapai maksimum. Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran Program Satuan Pendidikan Kelas/Semester : Matematika : IPA : SMA / MA : XII/1 Nama Guru NIP/NIK Sekolah : ........................... : ........................... : ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ............................. Mata Pelajaran : MATEMATIKA Kelas/Program : XII / IPA Semester :1 STANDAR KOMPETENSI: 1. Menggunakan konsep integral dalam pemecahan masalah. Kompetensi Dasar 1.1 Memahami konsep integral tak tentu dan integral tentu Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Kewirausahaan/ Ekonomi Kreatif Indikator Pencapaian Kompetensi Materi Pembelajaran Berorientasi tugas dan hasil Mengenal arti Integral tak tentu o Integral Tak entu Percaya diri Menurunkan sifatsifat integral tak tentu dari turunan o Integral Tentu Keorisinilan Menentukan integral tak tentu fungsi aljabar dan trigonometri Mengenal arti integral tentu Menentukan integral tentu dengan menggunakan sifat-sifat integral Menyelesaikan Kegiatan Pembelajaran Mengenal integral tak tentu sebagai anti turunan Menentukan integral tak tentu dari fungsi sederhana Merumuskan integral tak tentu dari fungsi aljabar dan trigonometri Merumuskan sifatsifat integral tak tentu Melakukan latihan integral tak tentu Mengenal integral tentu sebagai luas Penilaian Jenis Tagihan: Waktu 4x45’ Sumber Belajar Sumber: Tugas Individu Buku Paket Tugas Kelompok Ulangan Buku referensi lain Journal Bentuk Instrumen : Kuiz Tes Tertulis PG Tes Tertulis Uraian Internet Kompetensi Dasar Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Indikator Pencapaian Kompetensi Materi Pembelajaran masalah sederhana yang melibatkan integral tentu dan tak tentu Kegiatan Pembelajaran Penilaian Waktu Sumber Belajar daerah dibawah kurva Mendiskusiakan teorema dasar kalkulus Merumuskan sifat integral tentu Melakukan latihan soal integral tentu Menyelesaikan masalah aplikasi integral tak tentu dan integral tentu 1.2 Menghitung integral tak tentu dan integral tentu dari fungsi aljabar dan fungsi trigonometri yang sederhana Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan Demokratis Menetukan integral dengan dengan cara substitusi Menetukan integral dengan dengan cara parsial Menetukan integral dengan dengan cara substitusi trigonometri Teknik Pengintegralan: o Substitusi o Parsial o Substitusi Trigonometr i Membahas Integral sebagai anti deferensial Mengenal berbagai teknik pengintegralan (substitusi dan parsial) Menggunakan aturan integral untuk menyelesaikan masalah. Jenis Tagihan: 6x45’ Sumber: Tugas Individu Buku Paket Tugas Kelompok Ulangan Buku referensi lain Bentuk Instrumen : Kuiz Tes Tertulis PG Tes Tertulis Uraian Journal Internet Kompetensi Dasar 1.3 Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Indikator Pencapaian Kompetensi Menghitung luas suatu daerah ang dibatasi oelh kurva dan sumbu-sumbu pada koordinat. Menggunakan integral untuk menghitung luas daerah di bawah kurva dan volum benda putar Menghitung volume benda putar. Materi Pembelajaran o Luas Daerah o Volume Bend Putar Kegiatan Pembelajaran Mendiskusikan cara menentukan luas daerah dibawah kurva (menggambar daerahnya, batas integrasi) Menyelesaikan masalah luas daerah di bawah kurva Mendiskusikan cara menentukan volume benda putar (menggambar daerahnya, batas integrasi) Penilaian Jenis Tagihan: 12x45’ Sumber Belajar Sumber: Tugas Individu Buku Paket Tugas Kelompok Ulangan Buku referensi lain Journal Bentuk Instrumen : Kuiz Tes Tertulis PG Tes Tertulis Uraian Menyelesaikan masalah benda putar Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... Waktu NIP / NIK : .................................. Internet STANDAR KOMPETENSI: 2. Menyelesaikan masalah program linear. Kompetensi Dasar 2.1 Menyelesaikan sistem pertidaksamaan linear dua variabel Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Indikator Pencapaian Kompetensi Mengenal arti sistem pertidaksamaan linier dua variable Menentukan penyelesaian sistem pertidaksamaan linear dua variabel Materi Pembelajaran Program Linear Kegiatan Pembelajaran Penilaian Menyatakan masalah sehari-hari ke dalam bentuk sistem pertidaksamaan linear dengan dua peubah. Jenis Tagihan: Menentukan daerah penyelesaian pertidaksamaan linier Menyatakan himpunan penylesaian pertidaksamaan linear dua variabel Waktu 2x45’l Sumber Belajar Sumber: Buku Paket Tugas Individu Tugas Kelompok Buku referensi lain Ulangan Journal Internet Bentuk Instrumen : Kuiz Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar 2.2 Merancang model matematika dari masalah program linear Nilai Budaya Dan Karakter Bangsa Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis 2.3 Menyelesaikan model matematika dari masalah program linear dan penafsirannya Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Indikator Pencapaian Kompetensi Kewirausahaan/ Mengenal masalah yang merupakan program linier Materi Pembelajaran Kegiatan Pembelajaran Model Matematika Program Linier Mendiskusikan berbagai masalah program linear Penilaian Jenis Tagihan: Tugas Kelompok Buku referensi lain Ulangan Journal Menggambarkan daerah fisibel dari program linear Merumuskan model matematika dari masalah program linier Membuat model matematika dari suatu masalah aplikatif program linear Kuiz Tes Tertulis PG Tes Tertulis Uraian Mencari penyelesaian optimum sistem pertidaksamaan linear dengan menentukan titik pojok dari daerah fisibel atau menggunakan garis selidik. Jenis Tagihan: Menafsirkan solusi dari masalah program linier Menafsirkan penyelesaian dari masalah program linier. Buku Paket Menggambar daerah fisibel dari program linier Solusi Program Linier Sumber: Tugas Individu Menentukan fungsi objektif dan kendala dari program linier Menentukan nilai optimum dari fungsi objektif 6x45’ Sumber Belajar Membahas komponen dari masalah program linear: fungsi objektif, kendala Waktu Internet Bentuk Instrumen : 8x45’ Sumber: Buku Paket Tugas Individu Tugas Kelompok Buku referensi lain Ulangan Journal Internet Bentuk Instrumen : Tes Tertulis Kompetensi Dasar Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Indikator Pencapaian Kompetensi Materi Pembelajaran Kegiatan Pembelajaran Penilaian PG Tes Tertulis Uraian Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. Waktu Sumber Belajar STANDAR KOMPETENSI: 3. Menggunakan konsep matriks, vektor, dan transformasi dalam pemecahan masalah. Kompetensi Dasar 3.1. Menggunakan sifat-sifat dan operasi matriks untuk menunjukkan bahwa suatu matriks persegi merupakan invers dari matriks persegi lain Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Indikator Pencapaian Kompetensi Rasa ingin tahu Berorientasi tugas dan hasil Mengenal matrik persegi Mandiri Percaya diri Kreatif Keorisinilan Melakukan operasi aljabar atas dua matriks Kerja keras Demokratis Menurunkan sifatsifat operasi matriks persegi melalui contoh Mengenal invers matriks persegi Materi Pembelajaran Matriks Pengertian Matriks Operasi dan Sifat Matriks Matriks Persegi Kegiatan Pembelajaran Mencari data-data yang disajikan dalam bentuk baris dan kolom Menyimak sajian data dalam bentuk matriks Mengenal unsurunsur matriks Mengenal pengertian ordo dan jenis matriks Melakukan operasi aljabar matriks : penjumlahan, pengurangan, perkalian dan sifatsifatnya Mengenal matriks invers melalui perkalian dua matriks persegi yang menghasilkn matriks satuan Penilaian Jenis Tagihan: Waktu 4x45’ Sumber Belajar Sumber: Tugas Individu Buku Paket Tugas Kelompok Ulangan Buku referensi lain Journal Bentuk Instrumen : Kuiz Tes Tertulis PG Tes Tertulis Uraian Internet Kompetensi Dasar 3.2. Menentukan determinan dan invers matriks 2 x2 Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Indikator Pencapaian Kompetensi Menentukan diterminan matriks 2x2 Menentukan invers dari matrks 2x2 Materi Pembelajaran Determinan dan Invers matriks Kegiatan Pembelajaran Mendiskripsikan determinan suatu matriks Menggunakan algoritma untuk menentukan nilai determinan matriks pada soal. Menemukan rumus untuk mencari invers dari matriks 2x2 Penilaian Jenis Tagihan: Waktu 6x45’ Sumber Belajar Sumber: Tugas Individu Buku Paket Tugas Kelompok Ulangan Buku referensi lain Journal Bentuk Instrumen : Kuiz Tes Tertulis PG Tes Tertulis Uraian Internet Kompetensi Dasar 3.3. Menggunakan determinan dan invers dalam penyelesaian sistem persamaan linear dua variabel Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Indikator Pencapaian Kompetensi Materi Pembelajaran Menentukan persamaan matriks dari sistem persamaan linier Penerapan matrik pada sistem persamaan linier Menyelesaian sistem persamaan linear dua variabel dengan matriks invers Kegiatan Pembelajaran Menyajikan masalah sistem persamaan linier dalam bentuk matriks Menentukan invers dari matriks koefisien pada persamaan matriks Menyelesaikan persamaan lmatriks dari sistem persamaan linier 2 variabel Penilaian Jenis Tagihan: Waktu 8x45’ Sumber Belajar Sumber: Tugas Individu Buku Paket Tugas Kelompok Ulangan Buku referensi lain Journal Bentuk Instrumen : Kuiz Tes Tertulis PG Tes Tertulis Uraian Internet Kompetensi Dasar 3.4. Menggunakan sifat-sifat dan operasi aljabar vektor dalam pemecahan masalah Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Indikator Pencapaian Kompetensi Menjelaskan vektor sebagai besaran yang memilki besar dan arah Mengenal vektor satuan Menentukan operasi aljabar vektor : jumlah, selisih, hasil kali vektor dengan skalar, dan lawan suatu vektor Menjelaskan sifatsifat vektor secara aljabar dan geometri Menggunakan rumus perbandingan vektor Materi Pembelajaran Kegiatan Pembelajaran o Pengertian Vektor Mengenal besaran skalar dan vektor o Operasi dan siaft vektor Mendiskusikan vektor yang dapat dinyatakan dalam bentuk ruas garis berarah Melakukan kajian vektor satuan Melakukan operasi aljabar vector dan sifat-sifatnya Menyelesaiakn masalah perbandingan dua vector Penilaian Jenis Tagihan: Waktu 8x45’ Sumber Belajar Sumber: Tugas Individu Buku Paket Tugas Kelompok Ulangan Buku referensi lain Journal Bentuk Instrumen : Kuiz Tes Tertulis PG Tes Tertulis Uraian Internet Kompetensi Dasar 3.5. Menggunakan sifat-sifat dan operasi perkalian skalar dua vektor dalam pemecahan masalah. Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Indikator Pencapaian Kompetensi Menentukan hasilkali skalar dua vektor di bidang dan ruang Menjelaskan sifatsifat perkalian skalar dua vektor Materi Pembelajaran Perkalian skalar dua Vektor Kegiatan Pembelajaran Merumuskan defifnisi perkalian skalar dua vektor Menghitung hasil kali skalar dua vektor dan menemukan sifat-sifatnya Melakukan kajian suatu vector diproyeksikan pada vector lain Menentukan vektor proyeksi dan panjang proyeksinya Melakukan kajian menentukan sudut antara dua vektor Diskusi kelompok mencari permasalahan seharihari yang mempunyai penyelesaian dengan konsep vector. Penilaian Jenis Tagihan: Waktu 8x45’ Sumber Belajar Sumber: Tugas Individu Buku Paket Tugas Kelompok Ulangan Buku referensi lain Journal Bentuk Instrumen : Kuiz Tes Tertulis PG Tes Tertulis Uraian Internet Kompetensi Dasar 3.6. Menggunakan transformasi geometri yang dapat dinyatakan dengan matriks dalam pemecahan masalah Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Indikator Pencapaian Kompetensi Melakukan operasi berbagai jenis transformasi: translasi refleksi, dilatasi, dan rotasi. Menentukan persamaan matriks dari transformasi pada bidang. Materi Pembelajaran Transformasi Geometri Kegiatan Pembelajaran Mendefinisikan arti geometri dari suatu transformasi di bidang melalui pengamatan dan kajian pustaka Menentukan hasil transformasi geometri darsi sebuah titik dan bangun Menentukan operasi aljabar dari transformasi geometri dan mengubahnya kedalam bentuk persamaan matriks. Penilaian Jenis Tagihan: Waktu 8x45’ Sumber Belajar Sumber: Tugas Individu Buku Paket Tugas Kelompok Ulangan Buku referensi lain Journal Bentuk Instrumen : Kuiz Tes Tertulis PG Tes Tertulis Uraian Internet Kompetensi Dasar 3.7. Menentukan komposisi dari beberapa transformasi geometri beserta matriks transformasinya Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Indikator Pencapaian Kompetensi Menentukan aturan transformasi dari komposisi beberapa transformasi Menentukan persamaan matriks dari komposisi transformasi pada bidang. Materi Pembelajaran Komposisi Transformasi Geometri Kegiatan Pembelajaran Penilaian Mendefinisikan arti geometri dari komposisi transformasi di bidang Mendiskusikan aturan transformasi dari komposisi beberapa transformasi Menggunakan aturan komposisi transformasi untuk memecahkan masalah Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. Waktu 8x45’ Sumber Belajar Sumber: Buku Paket Buku referensi lain Journal Internet SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran Program Satuan Pendidikan Kelas/Semester : Matematika : IPA : SMA / MA : XII/2 Nama Guru NIP/NIK Sekolah : ........................... : ........................... : ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ............................. Mata Pelajaran : MATEMATIKA Kelas/Program : XII / IPA Semester :2 STANDAR KOMPETENSI: 4. Menggunakan konsep barisan dan deret dalam pemecahan masalah. Kompetensi Dasar 4.1. Menentukan suku ke-n barisan dan jumlah n suku deret aritmetika dan geometri Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Kewirausahaan/ Ekonomi Kreatif Indikator Pencapaian Kompetensi Berorientasi tugas dan hasil Menjelaskan arti barisan dan deret Pola Bilangan Mendiskusikan pola dan barisan bilangan Jenis Percaya diri Menemukan rumus barisan dan deret aritmatika Barisan Bilangan Merumuskan definisi barisan dan notasinya Barisan dan deret Aritmatika dan Geometri Merumuskan barisan aritmatika Tugas Individu Tugas Kelompo k Keorisinilan Menemukan rumus barisan dan deret geometri Mengehitung suku ke-n dan jumlah n suku deret aritmetika dan deret geometri. Materi Pembelajaran Kegiatan Pembelajaran Menghitung suku ke-n barisan aritmatika Merumuskan barisan geometri Menghitung suku ke-n barisan geometri Menghitung jumlah n suku pertama deret aritmetika dan Penilaian 4x45’ Tagihan : Ulangan Bentuk Instrum en: Waktu Kuiz Sumber Belajar Sumber: Buku Paket Buku referensi lain Journal Internet Kompetensi Dasar Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Indikator Pencapaian Kompetensi Materi Pembelajaran Kegiatan Pembelajaran deret geometri Mendiskusikan sisipan dari barisan aritmatika dan geometri Mendiskusikan deret geometri tak hingga 4.2. Menggunakan notasi sigma dalam deret dan induksi matematika dalam pembuktian 4.3. Merancang model matematika dari masalah yang berkaitan dengan deret - Rasa ingin tahu - Mandiri - Kreatif - Kerja keras - Demokratis - Rasa ingin tahu - Mandiri - Kreatif - Kerja keras - Demokratis - Berorientasi tugas dan hasil - Percaya diri - Keorisinilan - Berorientasi tugas dan hasil - Percaya diri - Keorisinilan o Menuliskan suatu deret dengan notasi sigma. o Menggunakan induksi matematika dalam pembuktian. Mengidentifikasi masalah yang berkaitan dengan deret. Merumuskan model matematika dari masalah deret Notasi Sigma Menyatakan suatu deret dengan notasi sigma Induksi Matematika Diskusi tentang pembuktian didalam matematika Model Matematika dari masalah deret Penilaian Tes Tertulis PG Tes Tertulis Uraian Waktu 8x45’ Menyatakan masalah yang merupakan masalah deret dan menentukan variabelnya Menyatakan kalimat verbal dari masalah deret ke dalam model matematika. Sumber: Buku Paket Buku referensi lain Menggunakan induksi matematika sebagai salah satu metode pembuktian dalam deret. Sumber Belajar Journal Internet 8x45’ Sumber: Buku Paket Buku referensi lain Journal Internet Kompetensi Dasar 4.4. Menyelesaikan model matematika dari masalah yang berkaitan dengan deret dan penafsirannya Kewirausahaan/ Nilai Budaya Dan Karakter Bangsa Ekonomi Kreatif - Rasa ingin tahu - - Mandiri Berorientasi tugas dan hasil - Percaya diri - Keorisinilan - Kreatif - Kerja keras - Demokratis Indikator Pencapaian Kompetensi Menentukan penyelesaiakan model matematika yang berkaitan dengan deret Memberikan tafsiran terhadap hasil penyelesaian yang diperoleh Materi Pembelajaran Solusi dari masalah deret Kegiatan Pembelajaran Mencari penyelesaian dari model matematika yang telah diperoleh Menafsirkan dari suatu masalah dengan penyelesaian yang berkaitan dengan deret barisan dan deret. Penilaian Waktu 10x45’ Sumber Belajar Sumber: Buku Paket Buku referensi lain Journal Internet STANDAR KOMPETENSI: 5. Menggunakan aturan yang berkaitan dengan fungsi eksponen dan logaritma dalam pemecahan masalah 5.1. Menggunakan sifat-sifat fungsi eksponen dan logaritma dalam pemecahan masalah. Kewirausahaan/ Nilai Budaya Dan Karakter Bangsa Kompetensi Dasar Rasa ingin tahu Mandiri Kreatif Kerja keras Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Demokratis Indikator Pencapaian Kompetensi Menghitung nilai fungsi eksponen dan logaritma Materi Pembelajaran Kegiatan Pembelajaran Penilaian Membahasa ulang arti eksponen dan logaritma dan syaratnya Jenis Menentukan sifatsifat fungsi eksponen dan logaritma Mendiskusikan dan menghitung nilai fungsi eksponen dan logaritma Tugas Individu Menyelesiakan masalah yang berkaitan dengan fungsi eksoponen dan logaritma. Menggunakan sifat-sifat fungsi eksponen dan logritma untuk menyelesaikan masalah Tugas Kelompo k Fungsi eksponen dan Logaritma Waktu 8x45’ Tagihan : Sumber Belajar Sumber: Buku Paket Buku referens i lain Journal Internet Ulangan Bentuk Instrum en: 5.2. Menggambar grafik fungsi eksponen dan logaritma. - Rasa ingin tahu - Mandiri - Kreatif - Kerja keras - Demokratis - Berorientasi tugas dan hasil - Percaya diri - Keorisinilan Menentukan nilai fungsi eksponen dan logaritma un tuk menggambar grafik Menemukan sifatsifat grafk fungsi Grafik Fungsi eksponen dan Logaritma Membuat tabel niali fungsi eksponen dan logaritma Menggambar sketsa grafik fungsi eksponen dan logaritma Menyelidiki sifat-sifat Kuiz Tes Tertulis PG Tes Tertulis Uraian 6x45’ Sumber: Buku Paket Buku referens i lain Kewirausahaan/ Nilai Budaya Dan Karakter Bangsa Kompetensi Dasar Ekonomi Kreatif Indikator Pencapaian Kompetensi Materi Pembelajaran Kegiatan Pembelajaran eksponen dan logaritma 5.3. Menggunakan sifat-sifat fungsi eksponen atau logaritma dalam penyelesaian pertidaksamaan eksponen atau logaritma sederhana - Rasa ingin tahu - Mandiri - Kreatif - Kerja keras - Demokratis - Berorientasi tugas dan hasil - Percaya diri - Keorisinilan Menentukan penyelesaian pertidaksamaan eksponen dan syaratnya Menentukan penyelesaian pertidaksamaan logaritma dan syaratnya Penilaian Waktu Journal grafik fungsi eksponen dan logaritma Pertidaksamaan Eksponen dan Logaritma Internet Mengidentitfikasi syarat dari pertidaksamaan eksponen dan logaritma Jenis Melakukan operasi aljabar untuk menyelesaikan pertidaksamaan logaritma Tugas Individu Tugas Kelompo k Menggunakan sifat-sifat fungsi logaritma untuk menyelesaikan masalah pertidaksamaan eksponen dan logaritma Sumber Belajar 8x45’ Tagihan : Ulangan Bentuk Instrume n: Kuiz Tes Tertulis PG Tes Tertulis Uraian Sumber: Buku Paket Buku referens i lain Journal Internet Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran Program Satuan Pendidikan Kelas/Semester : : : : Matematika Ilmu Pengetahuan Sosial SMA / MA XI/1 Nama Guru NIP/NIK Sekolah : : : ........................... ........................... ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ..................................... Mata Pelajaran : MATEMATIKA Kelas/Program : XI / IPS Semester :1 STANDAR KOMPETENSI: 1. Menggunakan aturan statistika, kaidah pencacahan, dan sifat-sifat peluang dalam pemecahan masalah. Kompetensi Dasar 1.1 Membaca data dalam bentuk tabel dan diagram batang, garis, lingkaran, dan ogive Materi Pokok/ Pembelajaran Diagram, Batang, diagram garis, Diagram Lingkaran dan Ogive Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Disiplin Berani mengambil resiko Demokratis Keorisinilan Kerja keras Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Mengamati dan mengidentifikasi tentang data-data di sekitar sekolah atau madrasah. Mengidentifikasi data-data yang dinyatakan dalam berbagai model. Mengelompokkan berbagai macam diagram dan tabel Menyimak konsep tentang penyajian data Membaca sajian data dalam bentuk diagram garis, dan diagram batang. Mengidentifikasi nilai suatu data yang ditampilkan pada tabel dan diagram Penilaian 4x45’ Jenis: Sumber Belajar Waktu Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar 1.2 Menyajikan data dalam bentuk tabel dan diagram batang, garis, lingkaran, dan ogive serta penafsirannya Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Penyajian Data Rasa ingin tahu Mandiri Berorientasi tugas dan hasil Melakukan latihan dalam berbagai penyajian data Percaya diri Disiplin Berani mengambil resiko Menafsirkan data dari berbagai macam bentuk. Demokratis Keorisinilan Mengambil kesimpulan dari dua atau lebih kelompok data atau informasi yang sejenis Kreatif Kerja keras Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Menyajikan data dalam bentuk diagram batang, garis, lingkaran, dan ogive serta penafsirannya Menafsirkan data dalam bentuk diagram batang, garis, lingkaran, dan ogive Penilaian Sumber Belajar Waktu 8x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian 1.3 Menghitung ukuran pemusatan, ukuran letak, dan ukuran penyebaran data, serta menafsirkannya Ukuran Pemusatan : Rataan, Modus, Median Rasa ingin tahu Mandiri Berorientasi tugas dan hasil Percaya diri Ukuran letak: Kuartil, desil Kreatif Ukuran Penyebaran: Janggkauan, simpangan kuartil, variansi dan simpangan baku Disiplin Berani mengambil resiko Demokratis Keorisinilan Kerja keras Mendiskusikan pentingnya penyajian data dalam bentuk histogram dan ogive Membuat tabel distribusi frekuensi dari data tertentu Menggambar grafik histogram dari tabel distribusi Menghitung ukuran pemusatan data baik data Membaca sajian data dalam bentuk tabel distribusi frekuensi dan histogram. Menyajikan data dalam bentuk tabel distribusi frekuensi dan histogram. Menentukan rataan, median, dan modus. 10x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif tunggal maupun data berkelompok. 1.4 Menggunakan aturan perkalian, permutasi, dan kombinasi dalam pemecahan masalah Aturan Perkalian, Permutasi dan Kombinasi Rasa ingin tahu Mandiri Kreatif Kerja keras Disiplin Demokratis Berdiskusi dengan kelompok untuk menyelesaikan soal-soal seharihari untuk mencari ukuran pemusatan data kemudian disajikan dalam bentuk diagram dan menafsirkan hasil yang didapat. Menentukan berbagai kemungkinan pengisian tempat (filling slot) dalam permainan tertentu atau masalahmasalah lainnya. Berorientasi tugas dan hasil Percaya diri Berani mengambil resiko Keorisinilan Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Berdiskusi mengenai kaidah pencacahan yang mengarah pada aturan perkalian, permutasi dan kombinasi. Menerapkan rumus aturan perkalian, permutasi, dan kombinasi untuk menyelesaikan soal Menyelesaikan Penilaian Sumber Belajar Waktu Uraian Memberikan tafsiran terhadap ukuran pemusatan. Menyusun aturan perkalian, permutasi dan kombinasi Menggunakan aturan perkalian, permutasi dan kombinasi 10x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Kegiatan Pembelajaran Ekonomi Kreatif Indikator Pencapaian Kompetensi Penilaian Sumber Belajar Waktu masalah-masalah yang berkaitan dengan aturan perkalian, permutasi dan kombinasi. 1.5 Menentukan ruang sampel suatu percobaan Ruang Sampel Rasa ingin tahu Mandiri Kreatif Berorientasi tugas dan hasil Percaya diri Disiplin Berani mengambil resiko Demokratis Keorisinilan Kerja keras Mendaftar titiktitik sampel dari suatu percobaan acak Menentukan ruang sampel dari percobaan acak tunggal dan kombinasi Menentukan banyak kemungkinan kejadian dari berbagai situasi Menuliskan himpunan kejadian dari suatu percobaan Menentukan banyaknya titik sampel 8x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian 1.6 Menentukan peluang suatu kejadian dan penafsirannya Peluang suatu Kejadian Rasa ingin tahu Mandiri Kreatif Kerja keras Disiplin Berorientasi tugas dan hasil Percaya diri Berani mengambil resiko Merancang dan melakukan percobaan untuk menentukan peluang suatu kejadian Menyimpulkan peluang kejadian Menentukan peluang kejadian melalui percobaan Menentukan peluang suatu kejadian secara 10x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Demokratis Kewirausahaan/ Kegiatan Pembelajaran Ekonomi Kreatif Keorisinilan dari percobaan yang dilakukan untuk mendukung peluang kejadian secara teoritisnya Menentukan peluang suatu kejadian, peluang komplemen suatu kejadian. Indikator Pencapaian Kompetensi teorotis Penilaian Ulangan Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Menentukan peluang suatu kejadian dari soal atau masalah sehari- hari. Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. Sumber Belajar Waktu Internet SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran Program Satuan Pendidikan Kelas/Semester : : : : Matematika Ilmu Pengetahuan Sosial SMA / MA XI/2 Nama Guru NIP/NIK Sekolah : : : ........................... ........................... ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ..................................... Mata Pelajaran : MATEMATIKA Kelas/Program : XI / IPS Semester :2 STANDAR KOMPETENSI: 2. Menentukan komposisi dua fungsi dan invers suatu fungsi. Kompetensi Dasar 2.1 Menentukan komposisi fungsi dari dua fungsi Materi Pokok/ Pembelajaran Komposisi Fungsi Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kegiatan Pembelajaran Membahas ulang pengertian fungsi Menjelaskan arti komposisi fungsi dalam konteks sehari-hari secara aljabar Kerja keras Mengidentifikasi fungsi-fungsi baik yang dapat atau tidak dapat dikomposisikan melalui contoh Menyimpulkan syarat komposisi fungsi Melakukan latihan soal fungsi komposisi yang bervariasi Menyelidiki dan Indikator Pencapaian Kompetensi Menentukan syarat dan aturan fungsi yang dapat dikomposisikan Menentukan fungsi komposisi dari beberapa fungsi. Menyebutkan sifat-sifat komposisi fungsi. Menentukan komponen pembentuk fungsi komposisi apabila fungsi komposisi dan komponen Penilaian 14x45’ Jenis: Sumber Belajar Waktu Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran sifat-sifat komposisi fungsi melalui contoh Menggunakan aturan komposisi dari beberapa fungsi untuk menyelesaikan masalah Menyelesaikan masalah yang berkaitan dengan komponen yang membentuk fungsi komposisi. Indikator Pencapaian Kompetensi lainnya diketahui. Penilaian Waktu Sumber Belajar Kompetensi Dasar 2.2 Menentukan invers suatu fungsi Materi Pokok/ Pembelajaran Invers Fungsi Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kegiatan Pembelajaran Kerja keras Melakukan kajian secara geometris untuk menentukan suatu fungsi mempunyai invers dan menyimpulkannya Menggambar sketsa grafik fungsi invers dari grafik fungsi asalnya Melakukan latihan menentukan fungsi invers dan grafiknya secara aljabar Menyelidiki sifat invers dari fungsi melalui contoh Menentukan invers dari komposisi fungsi Menerapkan aturan fungsi invers untuk menyelesaikan masalah. Indikator Pencapaian Kompetensi Menjelaskan syarat agar suatu fungsi mempunyai invers. Menggambar kan grafik fungsi invers dari grafik fungsi asalnya mengidentifikasi sifat-sifat fungsi invers. Menentukan fungsi invers dari suatu fungsi. Penilaian 10x45’ Jenis: Sumber Belajar Waktu Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian STANDAR KOMPETENSI: 3. Menggunakan konsep limit fungsi dan turunan fungsi dalam pemecahan masalah. Materi Pokok/ Kompetensi Dasar 3.1 Menghitung limit fungsi aljabar sederhana di suatu titik Pembelajaran Pengertian Limit Fungsi Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Kewirausahaan/ Kegiatan Pembelajaran Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Mendiskusikan arti limit fungsi di satu titik melalui perhitungan nilainilai di sekitar titik tersebut Mendiskusikan arti limit fungsi di tak berhingga melalui perhitungan nilainilai di sekitar titik tersebut Indikator Pencapaian Kompetensi Menjelaskan arti limit fungsi di satu titik melalui perhitungan nilai-nilai disekitar titik tersebut Menjelaskan arti limit fungsi di tak berhingga melalui grafik dan perhitungan. Penilaian Sumber Belajar Waktu 4x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian 3.2 Menggunakan sifat limit fungsi untuk menghitung bentuk tak tentu fungsi aljabar Sifat Limit Fungsi Rasa ingin tahu Bentuk Tak Tentu Kreatif Mandiri Kerja keras Berorientasi tugas dan hasil Menghitung limit fungsi aljabar Percaya diri Mengenal macammacam bentuk tak tentu Keorisinilan Melakukan perhitungan limit dengan manipulasi aljabar Menghitung limit fungsi aljabar di satu titik. Menjelaskan sifat-sifat yang digunakan dalam 8x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran Menghitung limit fungsi aljabar dengan menggunakan sifatsifat limit fungsi Indikator Pencapaian Kompetensi perhitungan limit. Menjelaskan arti bentuk tak tentu dari limit fungsi. Penilaian Sumber Belajar Waktu Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Menghitung limit fungsi aljabar dengan menggunakan sifat-sifat limit 3.3 Menggunakan sifat dan aturan turunan dalam perhitungan turunan fungsi aljabar Turunan Fungsi Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan Mengenal konsep laju perubahan nilai fungsi dan gambaran geometrisnya Menghitung limit fungsi yang mengarah ke konsep turunan. Dengan menggunakan konsep limit merumuskan pengertian turunan fungsi. Menjelaskan arti fisis (sebagai laju perubahan) dan arti geometri turunan di satu titik Dengan menggunakan aturan turunan menghitung turunan fungsi aljabar. Menurunkan sifatsifat turunan dengan menggunakani sifat Menghitung turunan fungsi yang sederhana dengan menggunakan definisi turunan Menentukan sisfat-sifat 8x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran Indikator Pencapaian Kompetensi lmit turunan fungsi Menentukan berbagai turunan fungsi aljabar Menentukan turunan fungsi dengan menggunakan aturan rantai Penilaian Sumber Belajar Waktu Menentukan turunan fungsi aljabar dengan menggunakan sifat-sifat turunan Melakukan latihan soal tentang turunan fungsi 3.4 Menggunakan turunan untuk menentukan karakteristik suatu fungsi aljabar dan memecahkan masalah Karakteristik Grafik Fungsi Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan Mengenal secara geometris tentang fungsi naik dan turun Mengidentifikasi fungsi naik atau fungsi turun menggunakan aturan turunan. Menggambar sketsa grafik fungsi dengan menentukan perpotongan sumbu koordinat, titik stasioner dan kemonotonannya Menentukan titik stasioner suatu fungsi beserta jenis Menentukan fungsi monoton naik dan turun dengan menggunakan konsep turunan pertama Menggambar sketsa grafik fungsi dengan menggunakan sifat-sifat turunan Menentukan titik ekstrim grafik fungsi 10x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Kegiatan Pembelajaran Ekonomi Kreatif ekstrimnya 3.5 Merancang model matematika dari masalah yang berkaitan dengan ekstrim fungsi aljabar Model matematika Ekstrim Fungsi Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan Menyelesaiakan persamaan garis singgung fungsi. Menyatakan masalah nyata dalam kehidupan sehari-hari dan membawanya ke konsep turunan. Menentukan variabel-variabel dari masalah ekstrim fungsi Mengembangkan statergi untuk merumuskan model matematika dari masalah ekstrim fungsi. Indikator Pencapaian Kompetensi Penilaian Sumber Belajar Waktu Menentukan persamaan garis singgung dari sebuah fungsi Mengidentifikasi masalah-masalah yang bisa diselesaiakn dengan konsep ekstrim fungsi Merumuskan model matematikan dari masalah ekstrim fungsi 10x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar 3.6 Menyelesaikan model matematika dari masalah yang berkaitan dengan ekstrim fungsi aljabar dan penafsirannya. Materi Pokok/ Pembelajaran Solusi masalah ekstrim Fungsi Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Kewirausahaan/ Kegiatan Pembelajaran Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Diskusi kelompok membahas soal aplikatif dengan menggunakan konsep turunan Menentukan penyelesaian dari model matematika beserta menafsirkannya Indikator Pencapaian Kompetensi Penilaian Menyelesaikan model matematika dari masalah ekstrim fungsi Jenis: Menafsirkan solusi dari masalah nilai ekstrim Tugas Kelompok 10x45’ Sumber: Kuiz Tugas Individu Buku Paket Buku referensi lain Ulangan Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... Sumber Belajar Waktu NIP / NIK : .................................. Journal Internet SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran Program Satuan Pendidikan Kelas/Semester : : : : Matematika Ilmu Pengetahuan Sosial SMA / MA XII/1 Nama Guru NIP/NIK Sekolah : : : ........................... ........................... ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ..................................... Mata Pelajaran : MATEMATIKA Kelas/Program : XII / IPS Semester :1 STANDAR KOMPETENSI: 1. Menggunakan konsep integral dalam pemecahan masalah sederhana. Kompetensi Dasar 1.1 Memahami konsep integral tak tentu dan integral tentu Materi Pokok/ Pembelajaran o Integral Tak tentu o Integral Tentu Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Mengenal integral tak tentu sebagai anti turunan Menentukan integral tak tentu dari fungsi sederhana Merumuskan integral tak tentu dari fungsi aljabar Merumuskan sifatsifat integral tak tentu Melakukan latihan integral tak tentu Mengenal integral tentu sebagai luas daerah di bawah kurva Mendiskusikan teorema dasar Merancang aturan integral tak tentu dari aturan turunan. Penilaian 10x45’ Jenis: Sumber Belajar Waktu Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Materi Pokok/ Kompetensi Dasar Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Penilaian Sumber Belajar Waktu kalkulus Merumuskan sifat integral tentu Melakukan latihan soal integral tentu Menyelesaikan masalah aplikasi integral tak tentu dan integral tentu 1.2 Menghitung integral tak tentu dan integral tentu dari fungsi aljabar sederhana Teknik Pengintegralan: o Substitusi o Parsial Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Berorientasi tugas dan hasil Percaya diri Keorisinilan Membahas Integral sebagai anti deferensial Mengenal berbagai teknik pengintegralan (substitusi dan parsial) Menggunakan aturan integral untuk menyelesaikan masalah. Menjelaskan integral tentu sebagai luas daerah di bidang datar. Menghitung integral tak tentu dari fungsi aljabar. 10x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar 1.3 Menggunakan integral untuk menghitung luas daerah di bawah kurva Materi Pokok/ Pembelajaran Menghitung luas daerah Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Mendiskusikan cara menentukan luas daerah di bawah kurva (menggambar daerahnya, batas integrasi) Menyelesaikan masalah luas daerah di bawah kurva Menghitung integral tentu dari fungsi aljabar Menghitung integral tentu dari fungsi aljabar Merumuskan integral tentu untuk luas suatu daerah dan menghitungnya . Penilaian Sumber Belajar Waktu 14x45’ Sumber: Buku Paket Buku referensi lain Journal Internet STANDAR KOMPETENSI: 2. Menyelesaikan masalah program linear Kompetensi Dasar 2.1 Menyelesaikan sistem pertidaksamaan linear dua variabel Materi Pokok/ Pembelajaran Program Linear Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Demokratis Kegiatan Pembelajaran Menyatakan masalah sehari-hari ke dalam bentuk sistem pertidaksamaan linear dengan dua peubah. Menentukan daerah penyelesaian pertidaksamaan linier Menyatakan himpunan penyelesaian pertidaksamaan linear dua variabel Indikator Pencapaian Kompetensi Mengenal arti sistem pertidaksamaa n linier dua variable Menentukan penyelesaian sistem pertidaksamaa n linear dua variabel Penilaian Sumber Belajar Waktu 12x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian 2.2 Merancang model matematika dari masalah program linear Model Matematika Program Linier Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Berorientasi tugas dan hasil Percaya diri Keorisinilan Mendiskusikan berbagai masalah program linear Membahas komponen dari masalah program linear: fungsi objektif, kendala Menggambarkan daerah fisibel dari program linear Membuat model matematika dari Mengenal masalah yang merupakan program linier Menentukan fungsi objektif dan kendala dari program linier Menggambar daerah fisibel dari program linier 14x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif suatu masalah aplikatif program linear 2.3 Menyelesaikan model matematika dari masalah program linear dan penafsirannya Solusi Program Linear Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Berorientasi tugas dan hasil Percaya diri Keorisinilan Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Mencari penyelesaian optimum sistem pertidaksamaan linear dengan menentukan titik pojok dari daerah fisibel atau menggunakan garis selidik. Menafsirkan penyelesaian dari masalah program linear. Merumuskan model matematika dari masalah program linear Menentukan nilai optimum dari fungsi objektif Menafsirkan solusi dari masalah program linear Penilaian Sumber Belajar Waktu Tes Tertulis PG Tes Tertulis Uraian 14x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian STANDAR KOMPETENSI: 3. Menggunakan matriks dalam pemecahan masalah. Kompetensi Dasar 3.1. Menggunakan sifat-sifat dan operasi matriks untuk menunjukkan bahwa suatu matriks persegi merupakan invers dari matriks persegi lain Materi Pokok/ Pembelajaran Matriks Pengertian Matriks Operasi dan Sifat Matriks Matriks Persegi Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Kegiatan Pembelajaran Mencari data-data yang disajikan dalam bentuk baris dan kolom Menyimak sajian data dalam bentuk matriks Mengenal unsur-unsur matriks Mengenal pengertian ordo dan jenis matriks Melakukan operasi aljabar matriks : penjumlahan, pengurangan, perkalian dan sifatsifatnya Mengenal matriks invers melalui perkalian dua matriks persegi yang menghasilkn matriks satuan 3.2. Menentukan determinan dan invers matriks 2 x2 Determinan dan Invers matriks Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Mendiskripsikan determinan suatu matriks Menggunakan algoritma untuk menentukan nilai determinan matriks Indikator Pencapaian Kompetensi Mengenal matrik persegi Melakukan operasi aljabar atas dua matriks Penilaian 8x45’ Kuiz Tugas Kelompok Mengenal invers matriks persegi Tes Tertulis Uraian Menentuka n invers dari matrks Sumber: Buku referensi lain Tugas Individu Ulangan Sumber Belajar Buku Paket Jenis: Menurunka n sifat-sifat operasi matriks persegi melalui contoh Menentuka n diterminan matriks 2x2 Waktu Journal Internet Bentuk Instrumen: Tes Tertulis PG 8x45’ Jenis: Kuiz Tugas Individu Tugas Kelompok Sumber: Buku Paket Buku referensi lain Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran pada soal. Indikator Pencapaian Kompetensi 2x2 Menemukan rumus untuk mencari invers dari matriks 2x2 Penilaian Waktu Sumber Belajar Ulangan Journal Bentuk Instrumen: Internet Tes Tertulis PG Tes Tertulis Uraian 3.3. Menggunakan determinan dan invers dalam penyelesaian sistem persamaan linear dua variabel Penerapan matrik pada sistem persamaan linier Rasa ingin tahu Berorientasi tugas dan hasil Mandiri Percaya diri Kreatif Keorisinilan Kerja keras Demokratis Menyajikan masalah sistem persamaan linier dalam bentuk matriks Menentukan invers dari matriks koefisien pada persamaan matriks Menyelesaikan persamaan matriks dari sistem persamaan linier 2 variabel Menentuka n persamaan matriks dari sistem persamaan linier Menyelesai an sistem persamaan linear dua variabel dengan matriks invers 10x45’ Jenis: Kuiz Tugas Individu Tugas Kelompok Ulangan Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. Sumber: Buku Paket Buku referensi lain Journal Internet SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran Program Satuan Pendidikan Kelas/Semester : : : : Matematika Ilmu Pengetahuan Sosial SMA / MA XII/2 Nama Guru NIP/NIK Sekolah : : : ........................... ........................... ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ..................................... Mata Pelajaran : MATEMATIKA Kelas/Program : XII / IPS Semester :2 STANDAR KOMPETENSI: 4. Menggunakan konsep barisan dan deret dalam pemecahan masalah. Materi Pokok/ Kompetensi Dasar 4.1 Menentukan suku ke-n barisan dan jumlah n suku deret aritmetika dan geometri Pembelajaran Nilai Budaya Dan Karakter Bangsa o Pola Bilangan Rasa ingin tahu o Barisan Bilangan Mandiri o Barisan dan deret Aritmatika dan Geometri Kreatif Kerja keras Demokratis Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran Berorientasi tugas dan hasil Mendiskusikan pola dan barisan bilangan Percaya diri Merumuskan definisi barisan dan notasinya Keorisinilan Merumuskan barisan aritmatika Menghitung suku ke-n barisan aritmatika Merumuskan barisan geometri Menghitung suku ke-n barisan geometri Menghitung jumlah n suku pertama deret aritmetika dan deret geometri Mendiskusikan Indikator Pencapaian Kompetensi Menjelaskan arti barisan dan deret Menemukan rumus barisan dan deret aritmatika Menemukan rumus barisan dan deret geometri Menghitung suku ke-n dan jumlah n suku deret aritmetika dan deret geometri. Penilaian 10x45’ Jenis: Sumber Belajar Waktu Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran Indikator Pencapaian Kompetensi Penilaian Sumber Belajar Waktu sisipan dari barisan aritmatika dan geometri Mendiskusikan deret geometri tak hingga 4.2 Merancang model matematika dari masalah yang berkaitan dengan deret Model Matematika dari masalah deret Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Berorientasi tugas dan hasil Percaya diri Keorisinilan Menyatakan masalah yang merupakan masalah deret dan menentukan variabelnya Menyatakan kalimat verbal dari masalah deret ke dalam model matematika. Mengidentifikasi masalah yang berkaitan dengan deret. Merumuskan model matematika dari masalah deret 10x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Materi Pokok/ Kompetensi Dasar Pembelajaran 4.3 Menyelesaikan model matematika dari masalah yang berkaitan dengan deret dan menafsirkan solusinya Solusi dari masalah deret Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Kegiatan Pembelajaran Percaya diri Keorisinilan Mencari penyelesaian dari model matematika yang telah diperoleh Menafsirkan penyelesaian dari suatu masalah yang berkaitan dengan barisan dan deret Indikator Pencapaian Kompetensi Menentukan penyelesaian model matematika yang berkaitan dengan deret Memberikan tafsiran terhadap hasil penyelesaian yang diperoleh Penilaian 14x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... Sumber Belajar Waktu NIP / NIK : .................................. SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran Program Satuan Pendidikan Kelas/Semester : : : : Matematika Bahasa SMA / MA XI/1 Nama Guru NIP/NIK Sekolah : : : ........................... ........................... ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ..................................... Mata Pelajaran : MATEMATIKA Kelas/Program : XI / BAHASA Semester :1 STANDAR KOMPETENSI: 1. Melakukan pengolahan, penyajian dan penafsiran data. Kompetensi Dasar 1.1 Membaca data dalam bentuk tabel dan diagram batang, garis, lingkaran, dan ogive serta pemaknaannya Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Statistika: Rasa ingin tahu diagram garis, diagram batang, diagram lingkaran , ogive dan histogram Mandiri Kreatif Kerja keras Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Demokratis Mengamati dan mengidentifikasi tentang data-data di sekitar sekolah. Mengidentifikasi datadata yang dinyatakan dalam berbagai model. Mengelompokkan berbagai macam diagram dan tabel. Menyimak konsep tentang penyajian data Membaca sajian data dalam bentuk diagram garis, dan diagram batang. Mengidentifika si nilai suatu data yang ditampilkan pada tabel dan diagram Penilaian 14x45’ Jenis: Sumber Belajar Waktu Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar 1.2 Menyajikan data dalam bentuk tabel dan diagram batang, garis, lingkaran, dan ogive serta pemaknaannya Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Statistika: Rasa ingin tahu diagram garis, diagram batang, diagram lingkaran , ogive dan histogram Mandiri Kreatif Kerja keras Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Melakukan latihan dalam berbagai penyajian data Menafsirkan data dari berbagai macam bentuk. Mengambil kesimpulan dari dua atau lebih kelompok data atau informasi yang sejenis Demokratis Menyajikan data dalam bentuk diagram batang, garis, lingkaran, dan ogive serta penafsirannya Menafsirkan data dalam bentuk diagram batang, garis, lingkaran, dan ogive Penilaian 16x45’ Jenis: Sumber Belajar Waktu Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar 1.3 Menghitung ukuran pemusatan, ukuran letak dan ukuran penyebaran data, serta menafsirkannya Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Ukuran Pemusatan : Rataan, Modus, Median Rasa ingin tahu Ukuran letak: Kuartil, desil Kerja keras Ukuran Penyebaran: Janggkauan, simpangan kuartil, variansi dan simpangan baku Mandiri Kreatif Demokratis Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Percaya diri Keorisinilan Mendiskusikan pentingnya penyajian data dalam bentuk histogram dan ogive Membuat tabel distribusi frekuensi dari data tertentu Membaca sajian data dalam bentuk tabel distribusi frekuensi dan histogram. Jenis: Menyajikan data dalam bentuk tabel distribusi frekuensi dan histogram. Ulangan Menentukan rataan, median, dan modus. Tes Tertulis Uraian Memberikan tafsiran terhadap ukuran pemusatan. Menggambar grafik histogram dari tabel distribusi Menghitung ukuran pemusatan data baik data tunggal maupun data berkelompok. Berdiskusi dengan kelompok untuk menyelesaikan soalsoal sehari-hari untuk mencari ukuran pemusatan data kemudian disajikan dalam bentuk diagram dan menafsirkan hasil yang didapat. Penilaian Sumber Belajar Waktu 20x45’ Sumber: Kuiz Tugas Individu Buku Paket Buku referensi lain Tugas Kelompok Bentuk Instrumen: Tes Tertulis PG Journal Internet Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran Program Satuan Pendidikan Kelas/Semester : : : : Matematika Bahasa SMA / MA XI/2 Nama Guru NIP/NIK Sekolah : : : ........................... ........................... ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ..................................... Mata Pelajaran : MATEMATIKA Kelas/Program : XI / BAHASA Semester :2 STANDAR KOMPETENSI: 2. Menggunakan kaidah pencacahan untuk menentukan peluang suatu kejadian dan penafsirannya. Kompetensi Dasar 2.1 Menggunakan sifat dan aturan perkalian, permutasi, dan kombinasi dalam pemecahan masalah Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Peluang: Rasa ingin tahu aturan perkalian Mandiri permutasi dan Kerja keras kombinasi Kreatif Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Kegiatan Pembelajaran Indikator Pencapaian Kompetensi Penilaian 14x45’ Keorisinilan Menentukan berbagai kemungkinan pengisian tempat (filling slot) dalam permainan tertentu atau masalah-masalah lainnya. Berdiskusi mengenai kaidah pencacahan yang mengarah pada aturan perkalian, permutasi dan kombinasi. Menerapkan rumus aturan perkalian, Menyusun aturan perkalian, permutasi, dan kombinasi Menggunakan aturan perkalian, permutasi, dan kombinasi Jenis: Sumber Belajar Waktu Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran Indikator Pencapaian Kompetensi Penilaian Sumber Belajar Waktu permutasi, dan kombinasi untuk menyelesaikan soal Menyelesaikan masalah-masalah yang berkaitan dengan aturan perkalian, permutasi dan kombinasi. 2.2 Menentukan ruang sampel suatu percobaan Ruang Sampel Rasa ingin tahu Mandiri Kreatif Kerja keras Berorientasi tugas dan hasil Percaya diri Keorisinilan Mendaftar titik-titik sampel dari suatu percobaan acak Menentukan banyak kemungkinan kejadian dari berbagai situasi Menentukan ruang sampel dari percobaan acak tunggal dan kombinasi Menuliskaaan himpunan kejadian dari suatu percobaan Menentukan jumlah titik sampel 16x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar 2.3 Menentukan peluang suatu kejadian dan menafsirkannya Materi Pokok/ Pembelajaran Peluang Kejadian Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Kegiatan Pembelajaran Percaya diri Keorisinilan Indikator Pencapaian Kompetensi Merancang dan melakukan percobaan untuk menentukan peluang suatu kejadian Menentukan peluang kejadian melalui percobaan Menyimpulkan peluang kejadian dari percobaan yang dilakukan untuk mendukung peluang kejadian secara teoritisnya Menentukan peluang suatu kejadian secara teoritis Menentukan peluang suatu kejadian, peluang komplemen suatu kejadian. Menentukan peluang suatu kejadian dari soal atau masalah sehari- hari. Penilaian 18x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... Sumber Belajar Waktu NIP / NIK : .................................. SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran Program Satuan Pendidikan Kelas/Semester : : : : Matematika Bahasa SMA / MA XII/1 Nama Guru NIP/NIK Sekolah : : : ........................... ........................... ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ..................................... Mata Pelajaran : MATEMATIKA Kelas/Program : XII/ BAHASA Semester :1 STANDAR KOMPETENSI: 1. Menyelesaikan masalah program linear Kompetensi Dasar 1.1. Menyelesaikan sistem pertidaksamaan linear dua variabel Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Program Linear Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Kegiatan Pembelajaran Menyatakan masalah sehari-hari ke dalam bentuk sistem pertidaksamaan linear dengan dua peubah. Menentukan daerah penyelesaian pertidaksamaan linear Menyatakan himpunan penyelesaian pertidaksamaan linear dua variabel Indikator Pencapaian Kompetensi Mengenal arti sistem pertidaksamaa n linear dua variable Menentukan penyelesaian sistem pertidaksamaa n linear dua variabel Penilaian 10x45’ Jenis: Sumber Belajar Waktu Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar 1.2. Merancang model matematika dari masalah program linear Materi Pokok/ Pembelajaran Model Matematika Program Linier Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu Mandiri Kreatif Kerja keras Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Demokratis Mendiskusikan berbagai masalah program linear Membahas komponen dari masalah program linear: fungsi objektif, kendala Menggambarkan daerah fisibel dari program linear Membuat model matematika dari suatu masalah aplikatif program linear 1.3. Menyelesaikan model matematika dari masalah program linear dan menafsirkan solusinya Solusi Program Linier Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Berorientasi tugas dan hasil Percaya diri Keorisinilan Indikator Pencapaian Kompetensi Kegiatan Pembelajaran Mencari penyelesaian optimum sistem pertidaksamaan linear dengan menentukan titik pojok dari daerah fisibel atau menggunakan garis selidik. Menafsirkan penyelesaian dari masalah program linear. Mengenal masalah yang merupakan program linear Menentukan fungsi objektif dan kendala dari program linear Menggambar daerah fisibel dari program linear Merumuskan model matematika dari masalah program linear Menentukan nilai optimum dari fungsi objektif Menafsirkan solusi dari masalah program linear Penilaian Sumber Belajar Waktu 15x45’ Jenis: Kuiz Tugas Individu Tugas Kelompok Ulangan Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian 15x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian STANDAR KOMPETENSI: 2. Menggunakan matriks dalam pemecahan masalah. Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Rasa ingin tahu 2.1. Menggunakan sifat-sifat dan operasi matriks untuk menunjukkan bahwa suatu matriks persegi merupakan invers dari matriks persegi lain Matriks Pengertian Matriks Operasi dan Sifat Matriks Mandiri Kreatif Kerja keras Kewirausahaan/ Ekonomi Kreatif Berorientasi tugas dan hasil Percaya diri Keorisinilan Kegiatan Pembelajaran Mencari data-data yang disajikan dalam bentuk baris dan kolom Menyimak sajian data dalam bentuk matriks Demokratis Mengenal unsur-unsur matriks Matriks Persegi Mengenal pengertian ordo dan jenis matriks Melakukan operasi aljabar matriks : penjumlahan, pengurangan, perkalian dan sifat-sifatnya Indikator Pencapaian Kompetensi Mengenal matriks persegi Melakukan operasi aljabar atas dua matriks Menurunkan sifat-sifat operasi matriks persegi melalui contoh Mengenal invers matriks persegi Determinan dan Invers matriks Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Berorientasi tugas dan hasil Mendiskripsikan determinan suatu matriks Percaya diri Keorisinilan Menggunakan algoritma untuk menentukan nilai determinan matriks pada soal. Sumber Belajar Waktu 8x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Mengenal matriks invers melalui perkalian dua matriks persegi yang menghasilkan matriks satuan 2.2. Menentukan determinan dan invers matriks 2 x2 Penilaian Tes Tertulis Uraian Menentukan diterminan matriks 2x2 Menentukan invers dari matrks 2x2 8x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran Indikator Pencapaian Kompetensi Menemukan rumus untuk mencari invers dari matriks 2x2 Penilaian Sumber Belajar Waktu Kelompok Ulangan Journal Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian 2.3. Menggunakan determinan dan invers dalam penyelesaian sistem persamaan linear dua variabel Penerapan matrik pada sistem persamaan linear Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Berorientasi tugas dan hasil Percaya diri Keorisinilan Menyajikan masalah sistem persamaan linier dalam bentuk matriks Menentukan invers dari matriks koefisien pada persamaan matriks Menyelesaikan persamaan matriks dari sistem persamaan linear 2 variabel Menentukan persamaan matriks dari sistem persamaan linear Menyelesaian sistem persamaan linear dua variabel dengan matriks invers 10x45’ Jenis: Sumber: Buku Paket Buku referensi lain Kuiz Tugas Individu Tugas Kelompok Journal Ulangan Internet Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... NIP / NIK : .................................. SILABUS PEMBELAJARAN PENDIDIKAN BUDAYA DAN KARAKTER BANGSA Mata Pelajaran Program Satuan Pendidikan Kelas/Semester : : : : Matematika Bahasa SMA / MA XII/2 Nama Guru NIP/NIK Sekolah : : : ........................... ........................... ........................... KURIKULUM TINGKAT SATUAN PENDIDIKAN (KTSP) SILABUS PEMBELAJARAN Nama Sekolah : ..................................... Mata Pelajaran : MATEMATIKA Kelas/Program : XII / BAHASA Semester :2 STANDAR KOMPETENSI: 3 Menggunakan konsep barisan dan deret dalam pemecahan masalah. Kompetensi Dasar o 3.1. Menentukan suku ke-n o barisan dan o jumlah n suku deret aritmetika dan geometri Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Pola Bilangan Rasa ingin tahu Barisan Bilangan Mandiri Barisan dan deret Aritmatika dan Geometri Kreatif Kerja keras Demokratis Kewirausahaan/ Ekonomi Kreatif Kegiatan Pembelajaran Berorientasi tugas dan hasil Mendiskusikan pola dan barisan bilangan Percaya diri Merumuskan definisi barisan dan notasinya Keorisinilan Merumuskan barisan aritmatika Menghitung suku ken barisan aritmatika Merumuskan barisan geometri Menghitung suku ken barisan geometri Menghitung jumlah n suku pertama deret aritmetika dan deret geometri Mendiskusikan sisipan dari barisan aritmatika dan Indikator Pencapaian Kompetensi Menjelaskan arti barisan dan deret Menemukan rumus barisan dan deret aritmatika Menemukan rumus barisan dan deret geometri Mengehitung suku ke-n dan jumlah n suku deret aritmetika dan deret geometri. Penilaian 16x45’ Jenis: Sumber Belajar Waktu Sumber: Buku Paket Buku referensi lain Journal Internet Kuiz Tugas Individu Tugas Kelompok Ulangan Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Kompetensi Dasar Materi Pokok/ Pembelajaran Nilai Budaya Dan Karakter Bangsa Kewirausahaan/ Kegiatan Pembelajaran Ekonomi Kreatif Indikator Pencapaian Kompetensi Penilaian Sumber Belajar Waktu geometri Mendiskusikan deret geometri tak hingga 3.2. Memecahkan masalah yang berkaitan dengan deret dan menafsirkan solusinya Solusi dari masalah deret Rasa ingin tahu Mandiri Kreatif Kerja keras Demokratis Berorientasi tugas dan hasil Percaya diri Keorisinilan Mencari penyelesaian dari model matematika yang telah diperoleh Menafsirkan dari suatu masalah dengan penyelesaian yang berkaitan dengan deret barisan dan deret. Menentukan penyelesaian model matematika yang berkaitan dengan deret Memberikan tafsiran terhadap hasil penyelesaian yang diperoleh 20x45’ Jenis: Buku Paket Buku referensi lain Journal Internet Kuiz Tugas Individu Tugas Kelompok Ulangan Bentuk Instrumen: Tes Tertulis PG Tes Tertulis Uraian Mengetahui, ..........., ............................ 20..... Kepala Sekolah......... Guru Mapel Matematika. (...........................................................) (.......................................................) NIP / NIK : .................................... Sumber: NIP / NIK : ..................................