(1) dan

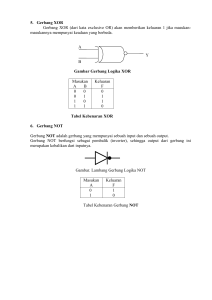
PERTEMUAN 3
GERBANG
LOGIKA
Sasaran
Pertemuan3
- Mahasiswa diharapkan dapat :
1. Mengerti tentang Gerbang Logika Dasar
2. Mengerti tentang Aljabar Boolean
3. Mengerti tentang Sum of Product dan
Product of Sum
Gerbang logika yaitu rangkaian dengan satu
atau lebih dari satu masukan tetapi hanya
menghasilkan satu keluaran
Semua kombinasi masukan dan keluaran
yang mungkin untuk sebuah rangkaian logika
ditunjukkan dalam Tabel logika / tabel
kebenaran (truth table)
Gerbang Logika Dasar
1. Inverter
A
Y
A
Y
0
1
1
0
In this animated
OR Logic example,
you can see that in
order to get light
through the house:
the left front door
OR the right front
door (or both) must
be Open.
OR GATE
ANIMATION
Same example: in order to block the light through the
house: the left front door AND the right front door must be
Closed.
2. OR GATE
A
0
0
1
1
B Y=A+B
0
0
1
1
0
1
1
1
The truth Table
OR GATE
ANIMATIONS SERIES
A
0
0
1
1
B Y=A+B
0
0
1
1
0
1
1
1
The truth Table
AND GATE
ANIMATION
In this animated
AND Logic
example of Doors
Opening and
Closing, you can
see that in order for
the "Light" to get
through the house,
the front door AND
the back door must
be Open.
Same example: if either the front door OR the back
door is Closed the light does NOT get through.
3. AND GATE
THE SYMBOL
A
0
0
1
1
B Y=A  B
0
0
1
0
0
0
1
1
The truth Table
A
B
Y
AND GATE
ANIMATIONS SERIES
A
0
0
1
1
B Y=A  B
0
0
1
0
0
0
1
1
The truth Table
Gerbang Logika Kombinasi
1. NOR
A
B
Y
A
0
0
1
1
B Y=A+B
0
1
1
0
0
0
1
0
2. NAND
A
B
Y
A
0
0
1
1
B Y=A  B
0
1
1
1
0
1
1
0
4. XOR GATE
A
Y
B
A
0
0
1
1
B Y=A  B
0
0
1
1
0
1
1
0
=
A
B
Y
4. XNOR GATE
A
B
A
0
0
1
1
Y
B Y=A  B
0
1
1
0
0
0
1
1
Atau
A
B
Y
4077 Quad
XNOR Gate
Gerbang logika lebih dari 2
masukan
Gelembung
inverter
A
B
C
Y
=
=
ALJABAR BOOLEAN
A. Hukum-hukum dan teori logika
1. hukum komutatif
a. A + B = B + A
b. A  B = B  A
2. hukum distributif
a. A  (B + C) = (A  B) + (A  C)
b. A + (B  C) = (A + B)  (A + C)
3. hukum assosiatif
a. A + B + C = A + (B + C)
= B + (A + C)
= C + (A + B)
b. A  B  C = A  (B  C)
= B  (A  C)
= C  (A  B)
4. hukum identitas
a. A + A = A
b. A  A = A
c. A  A  A = A
5. hukum absorbtif
a. A + (A  B) = A
b. A  (A + B) = A
c. A + (Ā  B) = A + B
d. A  (Ā + B) = A + B
6. Hukum Komplemen
a. A + Ā = 1
b. A  Ā = 0
7. Hukum Van De Morgan
_ _
a. A + B = A  B
_ _
b. A  B = A + B
8. Teori Logika
and
a. A  0 = 0
b. A  1 = A
c. A  A = A
d. A  Ā = 0
or
a. A + 0 = A
b. A + 1 = 1
c. A + A = A
d. A + Ā = 1
Ada 2 bentuk umum
dari ekspresi logika :
1. jumlah dari perkalian / sum of product
unsur dari sop disebut minimal term (minterm),
disimbolkan dengan huruf m
ĀB
+ ĀC +
minterm
m
A B C
ABC
m
2. Perkalian dari jumlah / product of sum
unsur dari pos disebut maximal term
disimbolkan dengan huruf M
Ā+B 
Minterm
A B C
Ā+C  A+B+C
M
M
(maxterm),
Soal : Buat Rumus untuk Nilai A
dan B
A=
B=
• Contoh1
Sederhanakan : A . (A . B + C) =
• Contoh 2
Sederhanakan : A’. B + A . B + A’. B’ =
• Contoh 3:
Sederhanakan : A + A . B’+ A’. B =
Contoh 4 :
Bila A=1, B=0, C=1 dan D=0 maka berapakah Q
=?
LATIHAN SOAL-SOAL
Ketentuan Pilihan :
a. Jika Pernyataan (1) dan (2) benar
b. Jika Pernyataan (1) dan (3) benar
c. Jika Pernyataan (2) dan (3) benar
a. Jika Pernyataan (1), (2), dan (3) benar
01. Ekspresi boolean untuk gerbang OR enam masukan
adalah :
(1). F = A+B+C+D+E+F
(2). Y = R+S+T+U+V+W
(3). Y = ABC + ABC
02. Ada 2 bentuk umum dari ekspresi logika yaitu
(1). Sum of Product
(2). Product of Sum
(3). Sum AND Product
02. Ada 2 bentuk umum dari ekspresi logika yaitu
(1). Sum of Product
(2). Product of Sum
(3). Sum AND Product
03. Untuk rangkaian yang lebih kompleks, gerbanggerbang dasar dapat disusun menjadi
(1). Rangkaian adder (penjumlah)
(2). Comparator (pembanding)
(3). Multiplexer / demultiplexer (pengubah data
paralel/serial menjadi data serial/ paralel)
03. Untuk rangkaian yang lebih kompleks, gerbanggerbang dasar dapat disusun menjadi
(1). Rangkaian adder (penjumlah)
(2). Comparator (pembanding)
(3). Multiplexer / demultiplexer (pengubah data
paralel/serial menjadi data serial/ paralel)
04. Rangkaian dasar yang dikombinasikan seperti
counter register dapat ditemukan pada alat berikut:
(1). Speedometer dan jam digital
(2). Kalkulator dan jam digital
(3). Timer
04. Rangkaian dasar yang dikombinasikan seperti
counter register dapat ditemukan pada alat berikut:
(1). Speedometer dan jam digital
(2). Kalkulator dan jam digital
(3). Timer
05.Bentuk rangkaian logika sederhana pada alat
speedomotor yang di seri dengan kunci kontak
adalah
(1). Sakelar
(2). Relay
(3). IC TTL dan IC CMOS
05.Bentuk rangkaian logika sederhana pada alat
speedomotor yang di seri dengan kunci kontak
adalah
(1). Sakelar
(2). Relay
(3). IC TTL dan IC CMOS
THE
END