gerak melingkar

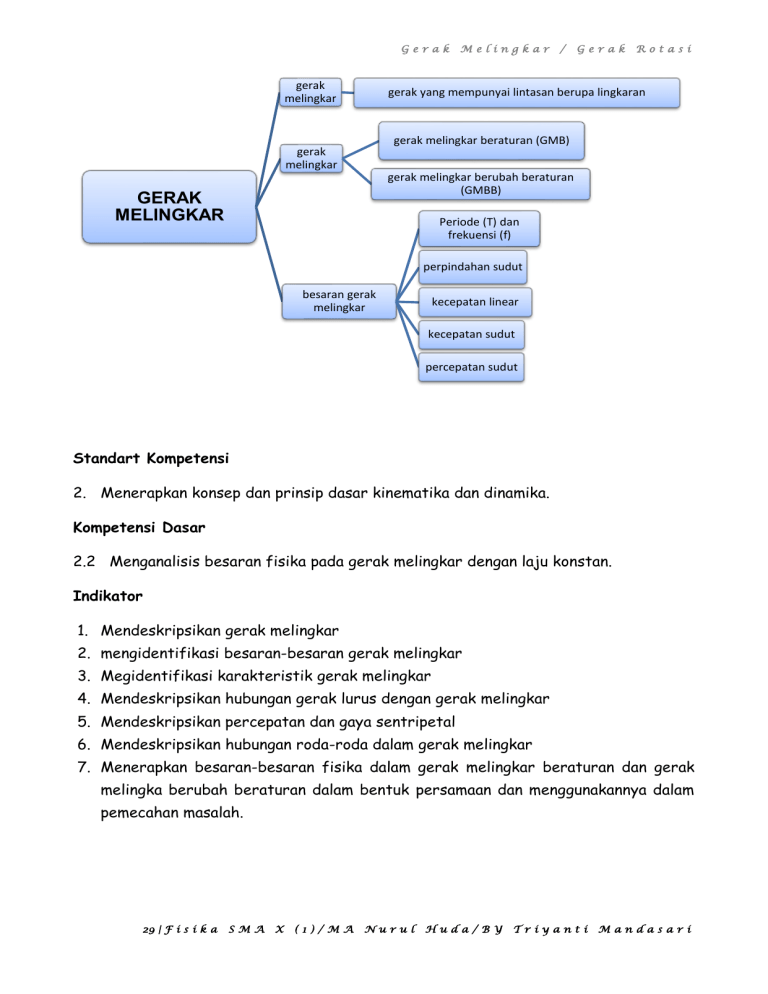
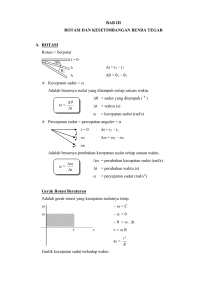
Gerak
gerak
melingkar
Melingkar
/
Gerak
Rotasi
gerak yang mempunyai lintasan berupa lingkaran
gerak melingkar beraturan (GMB)
gerak
melingkar
gerak melingkar berubah beraturan
(GMBB)
GERAK
MELINGKAR
Periode (T) dan
frekuensi (f)
perpindahan sudut
besaran gerak
melingkar
kecepatan linear
kecepatan sudut
percepatan sudut
Standart Kompetensi
2. Menerapkan konsep dan prinsip dasar kinematika dan dinamika.
Kompetensi Dasar
2.2 Menganalisis besaran fisika pada gerak melingkar dengan laju konstan.
Indikator
1. Mendeskripsikan gerak melingkar
2. mengidentifikasi besaran-besaran gerak melingkar
3. Megidentifikasi karakteristik gerak melingkar
4. Mendeskripsikan hubungan gerak lurus dengan gerak melingkar
5. Mendeskripsikan percepatan dan gaya sentripetal
6. Mendeskripsikan hubungan roda-roda dalam gerak melingkar
7. Menerapkan besaran-besaran fisika dalam gerak melingkar beraturan dan gerak
melingka berubah beraturan dalam bentuk persamaan dan menggunakannya dalam
pemecahan masalah.
29 | F i s i k a
SMA
X
(1)/MA
Nurul
Huda/BY
Triyanti
Mandasari
Gerak
Melingkar
/
Gerak
Rotasi
GERAK MELINGKAR
 Definisi gerak melingkar
Gerak melingkar (gerak
mempunyai
lintasan
rotasi)
berupa
adalah
lingkaran.
gerak
Pada
yang
gerak
melingkar, jarak tempuhnya berupa sudut yang disimbulkan
dengan 𝜃. Gerak melingkar sama halnya dengan gerak
lurus. Artinya, gerak melingkar juga dibagi menjadi dua:
gerak melingkar beraturan (GMB) dan gerak melingkar
berubah beraturan (GMBB)
 Besaran-besaran pada gerak melingkar
 Periode (T) dan frekuensi (f)
Periode adalah waktu yang diperlukan oleh benda untuk menempuh satu kali
putaran (satu lingkarang penuh).
Example:
Suatu benda untuk menempuh satu lingkaran penuh membutuhkan waktu 4
sekon. Artinya, periode benda tersebut 4 sekon.
Frekuensi adalah banyaknya lintasan satu lingkaran penuh yang ditempuh
benda dalam waktu satu sekon.
Rumus:
T =
𝒕
dan
𝒏
f =
𝒏
𝒕
Hubungan antara periode dan frekuensi:
T =
𝟏
dan
𝒇
f =
Keterangan:
T = periode (s)
n = jumlah putaran
Example:
𝟏
𝑻
f = frekuensi (Hz)
t = waktu tempuh (s)
Suatu benda menempuh lintasan satu lingkaran penuh sebnayak 3 kali putaran
dalam waktu 1 sekon. Artinya, frekuensi benda tersebut adalah 3 Hz.
 Perpindahan sudut (∆𝜽)
Perpindahan sudut adalah perpindahan partikel pada gerak melingkar.
Perpindahan sudut dapat dinyatakan dengan putaran atau radian.
1 putaran = 360o = 2𝜋 radian
1 radian =
30 | F i s i k a
180𝑜
𝜋
= 57,3𝑜
SMA
X
(1)/MA
Nurul
Huda/BY
Triyanti
Mandasari
Gerak
Melingkar
/
Gerak
Rotasi
 Kecepatan linear (v)
Kecepatan linear pada gerak melingkar sama seperti kecepatan pada gerak
lurus. Kecepatan linear adalah jarak yang ditempuh benda per satuan waktu.
Kecepatan linear (kecepatan tangensial) dimana arah kecepatan linear selalu
menyinggung lintasan putarannya.
𝑠
Gerak lurus
v=
𝑡
2𝜋𝑟
v=
Gerak melingkar
𝑇
= 2𝜋𝑟𝑓
Kecepatan linear adalah jarak yang ditempuh dibagi waktu tempuhnya (keliling
lingkaran dibagi periode gerak benda).
Keterangan:
r = panjang tali / jari-jari (m)
 Kecepatan sudut / kecepatan anguler (𝝎)
Kecepatan sudut adalah besarnya sudut yang ditempuh benda per satuan
waktu (rad/s).
Kecepatan sudut (𝜔) =
∆𝜃
∆𝑡
Satu putaran penuh pada lingkaran, sudut yang ditempuh adalah 360 o atau 2𝜋
rad dalam waktu T sekon, maka kecepatan sudut: 𝝎
=
𝟐𝝅
𝑻
= 𝟐𝝅𝒇
Keterangan:
𝜔 = kecepatan sudut (rad/s)
∆𝜃 = perpindahan sudut (rad)
∆𝑡 = selang waktu (s)
 Hubungan kecepatan linear (v) dengan kecepatan sudut (𝝎)
Kecepatan linear
v = 2𝜋𝑟𝑓
Kecepatan sudut
𝜔 = 2𝜋𝑓
Sehingga
v = 𝝎𝒓
 Percepatan sudut (𝜶)
Percepatan sudut (percepatan anguler) adalah perubahan kecepatan sudut
persatuan waktu.
Percepatan sudut (𝛼) =
31 | F i s i k a
SMA
X
∆𝜔
𝛼 = percepatan sudut (rad/s2)
∆𝑡
(1)/MA
Nurul
Huda/BY
Triyanti
Mandasari
Gerak
Melingkar
/
Gerak
Rotasi
Contoh Soal
1. Waktu yang diperlukan oleh benda untuk menempuh satu lingkaran penuh
adalah?
a. Percepatan sudut
c. Periode
e. kecepatan sudut
b. Frekuensi
d. Kecepatan linear
2. Jika kipas angin berputar sebanyak 2000 tiap 40 detik, maka periode dan
frekuensi putaran kipas angin tersebut adalah?
a. 50 s dan 0,02 Hz
d. 30 s dan 0,02 Hz
b. 20 s dan 0,002 Hz
e. 0,02 s s dan 40 Hz
c. 0,02 s dan 50 Hz
3. Baling-baling kipas angin berjari-jari
20
𝜋
cm mampu berputar 4 kali dalam satu
sekon. Kecepatan linear ujung baling-baling adalah? (UN)
a. 3,2 m/s
c. 1,3 m/s
b. 1,6 m/s
d. 1,0 m/s
e. 0,8 m/s
Kaji Soal
1. Jika suatu benda menempuh lintasan satu lingkaran penuh sebanyak 4 kali
putaran dalam waktu 2 detik. Berapakah frekuensi benda tersebut ..... Hz
a. 1
c. 3
b. 2
d. 4
e. 5
2. Sebuah benda bergerak melingkar beraturan dengan jari-jari 6 m. Jika dalam 2
menit benda itu melakukan 16 kali putaran maka kecepatan linear benda
tersebut adalah? (UN)
a. 0,8 𝜋 m/s
c. 1,2 𝜋 m/s
b. 1,0 𝜋 m/s
d. 1,4 𝜋 m/s
e. 1,6 𝜋 m/s
3. Sebuah benda bergerak melingkar dengan kecepatan sudut 50π rad/s.
Tentukan frekuensi putaran gerak benda!
4. Kecepatan sudut sebuah benda yang bergerak melingkar adalah 12 rad/s. Jika
jari-jari putarannya adalah 2 meter, tentukan besar kecepatan benda tersebut!
5. Roda yang jari-jarinya 20 cm berputar secara beraturan sehingga menempuh
120 putaran toap menit. Kecepatan linear suatu titik di tepi roda adalah.... (UN)
a. 0,8 𝜋 m/s
c. 12 𝜋 m/s
b. 4,8 𝜋 m/s
d. 24 𝜋 m/s
32 | F i s i k a
SMA
X
(1)/MA
Nurul
Huda/BY
e. 48 𝜋 m/s
Triyanti
Mandasari
Gerak
Melingkar
/
Gerak
Rotasi
6. Sebuah benda bergerak melingkar beraturan dengan jari-jari 3 m. Jika dalam 2
menit benda itu melakukan 8 kali putaran maka kecepatan linear benda tersebut
adalah? (UN)
a. 0,8 𝜋 m/s
c. 0,4 𝜋 m/s
b. 0,6 𝜋 m/s
e. 1,6 𝜋 m/s
e. 1,6 𝜋 m/s
7. Sebuah ban sepeda motor berjari-jari 35 cm. Jika ban tersebut menempuh sudut
4 𝜋 rad dalam waktu 0,5 s, kecepatan linear ban tersebut adalah? (UN)
a. 8,8 m/s
c. 20,4 m/s
b. 17,5 m/s
d. 35,5 m/s
e. 35,5 m/s
 Gerak melingkar
 Gerak Melingkar Beraturan (GMB)
GMB adalah gerak benda yang lintasannya melingkar dengan kecepatan
sudut tetap (𝝎) dan percepatan sudut benda nol (𝜶 = 𝟎).
Ciri-ciri:
 Kecepatannya sudut tetap (𝝎 = tetap)
 Percepatan sudut nol (𝜶 = 0)
 Lintasannya berupa lingkaran
𝜽 = 𝝎.t
Persamaan GMB
𝜃 = posisi sudut (rad)
Contoh Soal
1. Sebuah partikel bergerak melingkar dengan kecepatan sudut sebesar 4
rad/s selama 5 sekon. Tentukan besar sudut yang ditempuh partikel!
2. Sebuah benda yang bergerak melingkar beraturan mempunyai? (UN 2006/2007)
a. Kecepatan yang konstan, kelajuan berubah
b. Kelajuan yang konstan, kecepatan berubah
c. Percepatan yang konstan, gaya berubah
d. Sudut simpangan yang konstan
e. Gaya dan kecepatan yang konstan
3. Dalam gerak melingkar beraturan, percepatan berfunsi sebagai....
a. Mengubah arah
b. Memberi gaya tambahan
c. Menambah kecepatan benda
d. Mempertahankan arah kecepatan supaya tetap
e. Mempertahankan kelajuan benda
33 | F i s i k a
SMA
X
(1)/MA
Nurul
Huda/BY
Triyanti
Mandasari
Gerak
Melingkar
/
Gerak
Rotasi
 Gerak Melingkar Berubah Beraturan (GMBB)
GMBB adalah gerak benda yang lintasannya melingkar dengan kecepatan
sudut berubah-ubah (𝝎) dan percepatan sudut tetap (𝜶 = 𝒕𝒆𝒕𝒂𝒑).
Persamaan-persamaan GLBB
𝝎t = 𝝎𝟎 + 𝜶𝒕
keterangan:
𝟏
𝜽 = 𝝎𝟎 𝒕 + 𝟐 𝜶𝒕𝟐
𝜔0 = kecepatan sudut awal (rad/s)
𝝎t2 = 𝝎𝟎 2 + 2 𝜶𝜽
𝝎t = kecepatan sudut pada saat t (rad/s)
𝜽 = (
𝝎𝟎 +𝝎𝒕
𝟐
)𝒕
𝛼 = percepatan sudut (rad/s2)
1 rpm = 1 putaran per menit
Contoh Soal
1. Sebuah benda bergerak melingkar dengan percepatan sudut 2 rad/s 2. Jika
mula-mula benda diam, tentukan :
a. Kecepatan sudut benda setelah 5 sekon
b. Sudut tempuh setelah 5 sekon
2. Suatu mesin dengan tenaga listrik dapat mengerjakan roda dengan
kecepatan sudut 8 rad/s, kemudian listrik dipadamkan sampai gesekan kecil
pada poros roda menyebabkan perlambatan sudut tetap hingga roda
berhenti setelah 20 sekon. Jika jari-jari roda 20 cm tentukan perlambatan
sudutnya?
a. 0,1 rad/s2
c. 0,3 rad/s2
b. 0,2 rad/s2
d. 0,4 rad/s2
e. 0,5 rad/s2
Kaji Soal
1. Roda sepeda yang sedang berputar pada kecepatan 60 putaran permenit
direm sampai berhenti. Sejak pengereman sampai berhenti roda berputar 15
putaran. Hitung perlambatan yang dilakukan oleh roda !
2. Setelah motornya dimatikan, sebuah CD yang berputar dengan kecepatan
90 putaran permenit semakin lambat dan akhirnya berhenti dalam 30 sekon.
Tentukan percepatan sudutnya !
34 | F i s i k a
SMA
X
(1)/MA
Nurul
Huda/BY
Triyanti
Mandasari
Gerak
Melingkar
/
Gerak
Rotasi
 Hubungan gerak lurus dengan gerak melingkar
Gerak Lurus
Gerak Melingkar
Hubungan
s = jarak (m)
𝜃 = sudut jarak (rad)
s=𝜃r
v = kecepatan linear (m/s)
𝜔 = kecepatan sudut (rad/s)
v=𝜔r
a = percepatan linear (m/s2)
𝛼 = percepatan sudut (rad/s2)
a=𝛼r
Contoh Soal
1. Suatu mesin dengan tenaga listrik dapat mengerjakan roda dengan kecepatan
sudut 8 rad/s, kemudian listrik dipadamkan sampai gesekan kecil pada poros
roda menyebabkan perlambatan sudut tetap hingga roda berhenti setelah 20
sekon. Jika jari-jari roda 20 cm maka jarak linear mulai dari listrik padam sampai
berhenti adalah?
a. 8 m
c. 24 m
b. 16 m
d. 32 m
e. 40 m
 Percepatan dan gaya sentripetal
 Percepatan sentripetal (as)
Percepatan sentripetal adalah percepatan yang disebabkan oleh gaya
sentripetal. Arah percepatan sentripetal selalu menuju pusat lingkaran.
as =
𝒗𝟐
𝒓
=
(𝝎𝒓𝟐 )
𝒓
= 𝝎𝟐 𝒓
 Gaya sentripetal (Fs)
Gaya sentripetal adalah gaya yang menyebabkan benda bergerak melingkar.
Arahnya selalu ke pusat lingkaran.
Fs = m.as = m.
𝑣2
𝑟
= m.𝝎𝟐 𝒓
Keterangan:
Fs = gaya sentripetal (N)
m = massa benda (kg)
as = percepatan sentripetal (m/s2)
Contoh Soal
1. Sebuah benda bermassa 1 kg berputar dengan kecepatan sudut 120 rpm. Jika
jari-jari putaran benda adalah 2 meter tentukan percepatan sentripetal gerak
benda tersebut !
35 | F i s i k a
SMA
X
(1)/MA
Nurul
Huda/BY
Triyanti
Mandasari
Gerak
Melingkar
/
Gerak
Rotasi
2. Gaya sentripetal yang bekerja pada sebuah benda bermassa 1 kg yang sedang
bergerak melingkar beraturan dengan jari-jari lintasan sebesar 2 m dan
kecepatan 3 m/s adalah?
Kaji Soal
1. Sebuah benda yang massa 10 kg bergerak melingkar beraturan dengan
kecepatan 4 m/s. Jika jari-jari lingkaran 0,5 m maka:
4
(1) Frekuensi putarannya 𝜋
(2) Percepatan sentripetal 32 m/s2
(3) Gaya sentripetal 320 N
(4) Periode 4𝜋 sekon
Pernyataan yang benar adalah....... (UN)
a. (1), (2), (3) dan (4)
b. (1), (2), dan (3)
c. (1) dan (3)
d. (2) dan (4)
e. (3) dan (4)
2. Benda yang memiliki massa 2 kg bergerak secara beraturan dalam lintaran
melingkar berjari-jari 1 m dengan kecepatan 8 m/2.
(1) Percepatan sentripetal 128 m/s2
(2) Gaya sentripetal 128 N
(3) Periode 0,25 𝜋 sekon
Pernyataan yang benar berkaitan dengan gerak benda tersebut adalah....... (UN)
a. (1), (2) dan (3)
b. (1) dan (2)
c. (1) dan (3)
d. (2) dan (3)
e. (3)
 Hubungan roda-roda dalam gerak melingkar
 Satu poros / sepusat
Untuk dua roda yang dihubungkan sepusat (satu poros), arah putaran dan
kecepatan sudutnya sama. Pada sistem ini kelajuan sudutnya sama (𝜔𝐴 = 𝜔𝐵 ),
sedangkan kelajuan linear tidak sama (𝑣𝐴 ≠ 𝑣𝐵 ).
Sehingga
𝝎𝑨 = 𝝎𝑩
𝒗𝑨
𝒓𝑨
=
𝒗𝑩
𝒓𝑩
36 | F i s i k a
SMA
X
(1)/MA
Nurul
Huda/BY
Triyanti
Mandasari
Gerak
Melingkar
/
Gerak
Rotasi
Keterangan:
vA = kecepatan linear roda A (m/s)
vB = kecepatan linear roda B (m/s)
𝜔𝐴 = kecepatan sudut roda A (rad/s)
𝜔𝐵 = kecepatan sudut roda B (rad/s)
rA = jari – jari roda A (m)
rB = jari – jari roda B (m)
 Bersinggungan
Untuk dua roda yang dihubungkan bersinggungan, arah putaran kedua roda
berlawana dan kelajuan linear kedua sama. Pada sistem ini kelajuan sudutnya
sama (𝜔1 ≠ 𝜔2 ), sedangkan kelajuan linear tidak sama (𝑣1 = 𝑣2 ).
Sehingga
𝒗𝟏 = 𝒗𝟐
𝝎𝟏 𝒓𝑰 = 𝝎𝟐 𝒓𝟐
 Dihubungkan dengan tali
Untuk dua roda yang dihubungkan dengan tali, arah putaran kedua roda
berlawana dan kelajuan linear kedua sama. Pada sistem ini kelajuan sudutnya
sama (𝜔1 ≠ 𝜔2), sedangkan kelajuan linear tidak sama (𝑣1 = 𝑣2 ).
Sehingga
𝒗𝟏 = 𝒗𝟐
𝝎𝟏 𝒓𝑰 = 𝝎𝟐 𝒓𝟐
Contoh Soal
1. Dua buah roda dihubungkan dengan rantai, Jika jari jari roda pertama adalah
20 cm, jari-jari roda kedua adalah 10 cm dan kecepatan sudut roda pertama
adalah 50 rad/s, tentukan kecepatan sudut roda kedua!
37 | F i s i k a
SMA
X
(1)/MA
Nurul
Huda/BY
Triyanti
Mandasari
Gerak
Melingkar
/
Gerak
Rotasi
2. Dua buah roda berputar dihubungkan seperti pada gambar!
Jika kecepatan roda pertama adalah 20 m/s jari-jari roda
pertama dan kedua masing-masing 20 cm dan 10 cm,
tentukan kecepatan roda kedua!
3. Dua buah roda A dan B saling bersinggungan, masing-masing berjari-jari 10
cm dan 30 cm. Jika roda A berputar dengan frekuensi 8 Hz, maka frekuensi
roda B adalah?
Kaji Soal
1. Tiga buah roda berputar dihubungkan seperti gambar berikut!
Data ketiga roda :
r1 = 20 cm
r2 = 10 cm
r3 = 5 cm
Jika kecepatan sudut roda pertama adalah 100 rad/s, tentukan kecepatan
sudut roda ketiga!
2. Berdasarkan gambar berikut tentukan kecepatan sudut roda kedua?
3. Roda A dan roda B bersinggungan. Jari-jari roda A adalah 2 cm dan tiap menit
roda A berputar 20 kali, sedangkan roda B tiap menit berputar 13 kali. Jari-jari
roda B adalah....
a. 1,5 cm
c. 3 cm
b. 2,5 cm
d. 3,5 cm
e. 4 cm
4. Roda A dan B sepusat, masing-masing memiliki jari-jari 10 cm dan 15 cm.
Roda berputar dengan kecepatan sudut 4𝜋 rad/s. Apabila kecepatan sudut A
dijadikan 3/2 kali kecepatan sudut semula , frekuensi putaran roda B
menjadi....
a. Nol
c. 3/2 kali semula
b. 3/4 kali semula
d. 3 kali semula
38 | F i s i k a
SMA
X
(1)/MA
Nurul
Huda/BY
e. 4 akli semula
Triyanti
Mandasari