06. persamaan linier

06. PERSAMAAN LINIER
A Persamaan Linier dengan Satu Variabel
Persamaan linier dengan satu variabel mempunyai bentuk umum:
dimana:

, dan

adalah konstanta
Persamaan tersebut penyelesaiannya adalah:
Contoh soal:
1.
, berapakah x ?
Penyelesaian:
2.
, berapakah x ?
Penyelesaian:
3. Jumlah dari dua bilangan adalah 21, dan salah satu bilangan tersebut adalah dua kali bilangan
lainnya. Carilah bilangan-bilangan tersebut !
Penyelesaian:
Misalkan bilangan yang dicari adalah x dan 2x, maka:
Jadi bilangan itu adalah
dan
4. Empat kali suatu bilangan tertentu dikurangi 10 adalah 14. Tentukan bilangan tersebut
Penyelesaian:
Misalkan bilangan yang dikehendaki adalah x, maka:
Matematika: PERSAMAAN LINIER - Sugiyono | 1
5. Jumlah dari tiga bilangan bulat yang berurutan adalah 24. Carilah bilangan-bilangan tersebut!
Penyelesaian:
Misalkan tiga bilangan tersebut adalah ,
, dan
, maka:
Jadi bilangan-bilangan bulat tersebut adalah:



6. Ali mempunyai 50 keping, dalam lima ratusan rupiah dan seribuan rupiah, semuanya
berjumlah Rp. 35.000,--. Berapa keping uang lima ratusan yang dimilikinya ?
Penyelesaian:
Misalkan jumlah uang lima ratusannya adalah
adalah
keping, maka jumlah uang seribuannya
keping.
Jumlah uang lima ratusan + jumlah uang seribuan = Rp. 35.000 maka:
Jadi uang lima ratusan yang dimiliki Ali adalah
keping.
7. Berapakah berat air yang harus diuapkan dari 40 kg larutan garam 20% untuk menghasilkan
larutan garam 50%? (catatan: % dalam satuan berat per-berat, dan yang diuapkan adalah air
jadi berat garamnya tetap).
Penyelesaian:
Matematika: PERSAMAAN LINIER - Sugiyono | 2
Untuk larutan garam 20% (artinya berat garamnya 20% dari berat larutan) seberat 40 kg,
misalnya berat garam a kg, dan airnya b kg, maka:

Berat garam

Berat air
Misalkan air yang diuapkan adalah
agar kadar larutan garam menjadi 50%.
Rumus kadar larutan garam adalah:
Maka air yang harus diuapkan
untuk memperoleh kadar larutan 50% adalah:
Jadi untuk memperoleh kadar larutan garam 50% harus menguapkan air
TUGAS:
Selesaikan soal-soal berikut ini:
1. Di dalam dompet terdapat uang berjumlah Rp. 170.000, terdiri atas lima ribuan, sepuluh ribuan,
dan dua puluh ribuan rupiah. Banyaknya sepuluh ribuan rupiah adalah dua kali banyaknya dua
puluh ribuan, dan banyaknya lima ribuan rupiah kurang dua dari dua kali banyaknya sepuluh
ribuan. Tentukan banyaknya masing-masing lembar uang tersebut.
2. Berapakah bonus yang harus diterima oleh seorang karyawan sedemikian rupa sehingga ia
menerima bersih Rp. 500.000, setelah dikurangi pajak 15%.
3. Berapa harga yang harus dipasang oleh seorang pedagang roti yang harga belinya Rp. 12.000,
agar dapat memberikan potongan 20% dan masih mendapatkan untung 25%.
4. Harga donat super adalah Rp. 3.500 dan harga donat mini adalah Rp. 2.000. Pada suatu hari,
counter makanan itu menjual 280 porsi donat dan jumlah uang yang diperoleh Rp. 875.000.
Berapakah banyaknya donat mini yang terjual pada hari itu?
Matematika: PERSAMAAN LINIER - Sugiyono | 3
5. Seorang karyawan digaji Rp. 20.000 untuk setiap hari kerja dan didenda Rp. 5.000 untuk setiap
hari absen. Pada akhir hari ke-25 ia mendapat gaji bersih Rp. 450.000. Berapa harikah dia
bekerja?
6. Sebuah laporan tenaga kerja mengatakan bahwa suatu perusahaan mempekerjakan 400 orang lakilaki dan perempuan. Rata-rata gaji harian untuk seorang laki-laki adalah Rp. 20.000 dan untuk
seorang perempuan Rp. 15.000. Apabila biaya untuk tenaga kerja adalah Rp. 7.150.000 per hari,
berapakah jumlah tenaga kerja perempuan?
7. Berapakah berat air yang harus ditambahkan pada 5.000 liter larutan alkohol 90% untuk
menghasilkan larutan 70%? Semua persen menurut berat. (kurang jelas !!!)
8. Kacang tanah basah sebanyak 30 kg mempunyai kadar air 50 %. Berapa berat air yang harus
diuapkan untuk menghasilkan kacang tanah kering dengan kadar air 10 % ?
Jika kadar protein kacang tanah mula-mula (kacang tanah basah) 10 %, berapa kadar protein
kacang tanah kering ? (dianggap protein tidak mengalami kerusakan selama proses pengeringan).
9. Sebungkus mie instan dengan berat 84 g mempunyai kadar lemak 23 %, karbohidrat 57 %,
protein 11 %, dan bahan-bahan lain yang dianggap tidak menghasilkan energi. Tiap gram lemak,
karbohidrat, dan protein masing-masing menghasilkan 9, 4, dan 4 kkal (kilo kalori). Jika
kebutuhan energi 2.000 kkal/hari dan anda hanya makan mie instan, berapa bungkus kebutuhan
mie instan per hari ?
10. Minuman serbuk instan mengandung pemanis buatan aspartam sebanyak 120 mg/sachet. Menurut
ketentuan, aspartam boleh dikonsumsi maksimal 40 mg/kg berat badan/hari. Jika anda
mempunyai berat badan 48 kg, berapa sachet maksimal minuman serbuk instan yang boleh anda
konsumsi per hari ?
11. Sebuah perusahaan mempunyai pegawai sebanyak 30 orang terdiri dari seorang manager, tiga
orang supervisor dan sisanya karyawan dengan gaji per bulan masing-masing Rp. 3.000.000,00;
Rp. 1.500.000,00; dan Rp. 500.000,00. Karena inflasi, perusahaan menaikkan gaji masing-masing
Rp. 150.000,00. Berapa % total kenaikan gaji perusahaan ?
B Persamaan Linier Dua Variabel (PLDV)
Persamaan linier dua variabel adalah persamaan yang mengandung dua variabel dimana
pangkat/derajat setiap variabelnya sama dengan satu. Jadi persamaan-persamaan yang tidak
termasuk persamaan linier adalah:

Persamaan yang mempunyai pangkat selain satu (misalnya,

Persamaan yang mempunyai produk dua variabel (misalnya,
)
Bentuk umum persamaan linier dua variabel (PLDV) adalah:
Matematika: PERSAMAAN LINIER - Sugiyono | 4
dimana:



disebut variabel-variabel
dan
C Sistem Persamaan Linier Dua Variabel (SPLDV)
Sistem persamaan linier dua variabel adalah dua persamaan linier dua variabel (2 PLDV) yang
mempunyai hubungan diantara keduanya dan mempunyai satu penyelesaian.
Bentuk umum SPLDV adalah:
dimana:

disebut variabel

disebut koefisien

disebut konstanta
D Penyelesaian SPLDV
1. Metode Substitusi
Menggantikan satu variabel dengan variabel dari persamaan yang lain.
Contoh:
Carilah penyelesaian sistem persamaan:
dan
Penyelesaian:

Kita ambil persamaan pertama yang akan disubstitusikan yaitu

Kemudian persamaan tersebut kita ubah menjadi

Kemudian persamaan yang diubah tersebut disubstitusikan ke persamaan
-y=6

Kemudian masukkan nilai
tersebut ke dalam salah satu persamaan:
Matematika: PERSAMAAN LINIER - Sugiyono | 5

Jadi penyelesaian sistem persamaan tersebut adalah
dan
.
Himpunen penyelesaiannya : HP = {4, 2}
2. Metode Elmininasi
Dengan cara mengeliminasi salah satu variabel
atau .
Contoh:
Selesaikan soal di atas dengan cara eliminasi!
Penyelesaian:

Mengeliminasi variabel
2 

1 


Masukkan nilai
ke dalam salah satu persamaan.
Jadi HP = {4, 2}

Mengeliminasi variabel
1 

2 


Masukkan nilai
ke dalam salah satu persamaan.
Jadi HP = {4, 2}
Matematika: PERSAMAAN LINIER - Sugiyono | 6
Contoh aplikasinya:
Harga dua buah mangga dan tiga buah jeruk adalah Rp. 6.000,-- kemudian apabila membeli
lima buah mangga dan empat buah jeruk adalah Rp. 11.500,--. Berapa jumlah uang yang
harus dibayar apabila kita membeli empat buah mangga dan lima buah jeruk?
Penyelesaian:
Dalam menyelesaikan persoalan cerita seperti di atas diperlukan penggunaan model
matematika.
Misal harga 1 buah mangga adalah
dan harga 1 buah jeruk adalah , maka model
matematika soal tersebut adalah:
Ditanyakan:
Eliminasi variabel , sebagai berikut:
5 

2 


Masukkan ke dalam salah satu persamaan:
Jadi uang yang harus dibayarkan untuk membeli 4 buah mangga dan 5 buah jeruk adalah:
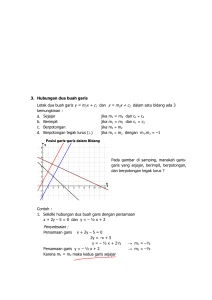
3. Menggunakan Grafik Garis Lurus
Penyelesaiannya didapatkan dengan menggunakan titik potong antara dua garis lurus tersebut
pada grafik garis lurus.
Contoh (sama dengan contoh di atas):
Tentukanlah penyelesaian dari
dan
Penyelesaian:
(1)
(2)
Langkah-langkah penyelesaiannya adalah sebagai berikut:

Menentukan titik-titik potong kedua persamaan tersebut dengan sumbu
dan .
Matematika: PERSAMAAN LINIER - Sugiyono | 7
Persamaan (1):
Berpotongan dengan sumbu , jika
, maka:
Berpotongan dengan sumbu , jika
, maka:
Tabel rangkuman hasil hitung:
8
0
0
4
Persamaan (2):
Berpotongan dengan sumbu , jika
, maka:
Berpotongan dengan sumbu , jika
, maka:
Tabel rangkuman hasil hitung:
3
0
0
-6
Matematika: PERSAMAAN LINIER - Sugiyono | 8

Membuat grafik garis lurus menggunakan tabel-tabel di atas:

Menentukan titik potong kedua persamaan tersebut:
Terlihat titik potongnya adalah
dan
Jadi HP = {4, 2}
Matematika: PERSAMAAN LINIER - Sugiyono | 9
4. Metode Determinan
Determinan diberi lambang
atau
a. Bentuk umum
keterangan:
:
elemen determinan
:
baris
:
kolom
b. Determinan orde dua
c. Determinan orde tiga
(1)
Definisi Saurus (menulis kolom I dan II di belakang kolom III)
(2)
Dengan perhitungan
Matematika: PERSAMAAN LINIER - Sugiyono | 10
Bentuk umum SPLDV adalah:
Cara penyelesaian dengan metode determinan:
Nilai
adalah:
Nilai
adalah:
Untuk contoh soal di atas:
(1)
(2)
Jadi HP = {4, 2}
Matematika: PERSAMAAN LINIER - Sugiyono | 11