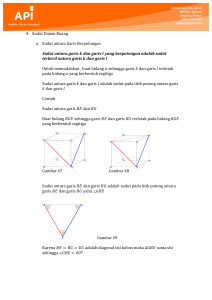
Memahami Hubungan Antar Sudut

GARIS DAN SUDUT
(Materi SMP Kelas VII Semester1)
Garis dan Sudut
Memahami Kedudukan Garis dan Sudut
a. Menemukan konsep titik, garis, dan bidang
Dalam ilmu Geometri, terdapat beberapa istilah atau sebutan yang tidak
memiliki
definisi (undefined terms), antara lain, titik, garis, dan bidang.Meskipun ketiga istilah
tersebut tidak secara formal didefinisikan, sangat penting disepakati tentang arti istilah
tersebut.
Perhatikan gambar berikut ini.
Titik tidak memiliki ukuran, biasanya dideskripsikan menggunakan tanda noktah,seperti
pada gambar di atas. Penamaan titik menggunakan huruf kapital, seperti titikA, titik B,
titik C, dan sebagainya.
Sedangkan, garis direpresentasikan oleh suatu garis lurus dengan dua tanda panah di
setiap ujungnya yang mengindikasikan bahwa garis tersebut panjangnya tak terbatas.
Suatu bidang direpresentasikan oleh permukaan meja atau dinding. Pada Gambar
Selanjutnya, beberapa konsep dasar dalam geometri juga harus dipahami tanpa
didefinisikan. Salah satu diantaranya, konsep letak suatu titik pada suatu garis atau pada
suatu bidang.
Mari perhatikan gambar di bawah ini.
1. Posisi titik terhadap garis
2. Posisi titik terhadap bidang
3. Titik-titik segaris
Dua atau lebih dikatakan segaris jika titik-titik tersebut terletak pada garis yang sama.
Pada Gambar 4.3 titik A dan titik B dikatakan segaris, karena sama-sama terletak pada
garis l.
4. Titik-titik sebidang
Dua atau lebih dikatakan sebidang jika titik-titik tersebut terletak pada bidang yang sama.
Pada Gambar 4.5 titik C dan titik D dikatakan sebidang, karena sama-sama terletak pada
bidang ß.
Gambar 4.6 di atas adalah kondisi daerah yang dihubungkan oleh sebuah jembatan. Jembat
merupakan struktur penghubung antara dua tempat yang terpisah. Jembatan berperan sebagai
penghubung dua daerah yang dipisahkan oleh sungai. Andaikan sisi kiri sungai sebagai titik A,
sisi kanan sungai sebagai titik B dan ruas garis AB merepresentasikan jembatan itu sendiri.
Adanya ruas garis AB menjadikan dua titik A dan B terhubung. Jika titik A merupakan titik
pangkal ruas segmen garis AB, maka titik B merupakan titik ujung ruas garis AB.
Masalah lain yang akan kita pahami berikutnya adalah cahaya yang dihasilkan senter. Mari
cermati Gambar 4.7.
Mari kita fokus pada cahaya yang memancar lurus dan besar (garis kuning). Tentunya, pangkal
dari cahaya tersebut adalah senter. Jika kita hanya perhatikan pada gambar, kita dapat
menentukan ujung cahaya, tetapi pada kejadian sebenarnya cahaya tersebut tidak memiliki
ujung.
Jadi pada kejadian ini, kita menemukan suatu pengamatan terhadap objek yang memiliki titik
awal, tetapi tidak memiliki ujung.
Dari tiga kajian di atas, terdapat dua pemahaman yang berkaitan dengan garis, segmen garis, dan
sinar garis (sinar).
Secara geometri, ketiga istilah tersebut kita deskripsikan sebagai berikut.
⃡
Gambar di bawah ini adalah garis yang melalui titik A dan B disebut garis AB, dinotasikan 𝐴𝐵
⃡ artinya dapat diperpanjang sampai tak terbatas.
Tanda panah pada kedua ujung 𝐴𝐵
̅̅̅̅, dengan titik A dan B
Gambar di bawah ini adalah ruas garis (segmen) AB, disimbolkan 𝐴𝐵
merupakan titik ujung ruas garis AB.
b. Kedudukan Garis
Pembahasan pada buku ini, kalian akan lebih banyak menggunakan garis daripada dua yang lain.
Alasannya, semua kajian matematika harus berlaku secara umum, bukan hanya pada sebagian.
Selanjutnya kita akan mengkaji posisi satu garis dengan garis yang lain.
1. Garis Berpotongan
Dua buah garis akan berpotongan jika memiliki tepat satu titik persekutuan. Misalkan terdapat
dua garis yakni AB dan CD, maka kondisi berpotongan dapat digambarkan sebagai berikut:
2. Garis Sejajar
Kondisi sejajar akan terjadi jika dua garis berada di bidang yang sama dan tidak memiliki
persekutuan. Contoh dua garis yang sejajar adalah sebagai berikut:
3. Garis Berhimpit
Kondisi berhimpit akan terjadi jika dua garis terletak pada satu garis lurus, sehingga
seolah-olah hanya terdapat satu garis saja.
Contoh garis yang saling berhimpit
Cermati kembali Gambar 4.9, untuk satuan waktu 24 jam.
1. Ada berapa kali dapat ditemukan garis (jarum jam, menit dan detik) berhimpit?
2. Ada berapa kali terbentuk sudut siku-siku (90˚) antara jarum menit dan jarum jam?
Untuk membantu kita memahami lebih mudah tentang kedudukan garis, mari cermati setiap
gambar di bawah ini.
Pada Gambar 4.10 (i), titik P merupakan pertongan garis l dan garis k.
Sedangkan pada Gambar 4.10 (ii), titik P merupakan perpotongan garis k, l dan m. Selain titik,
terdapat juga daerah-daerah yang terbentuk oleh garis-garis yang berpotongan tersebut. Untuk
Gambar 4.10 (i) terdapat 4 daerah yang terbentuk oleh hasil perpotongan garis k dan garis l, serta
Gambar 4.10 (ii) menghasilkan 6 daerah yang terbentuk oleh hasil perpotongan ketiga garis
tersebut.
Gambar 4.11 berikut ini, menyajikan garis-garis yang saling sejajar. Ciri yang menunjukkan
dua atau tiga garis (terletak pada satu bidang datar) saling sejajar jika jarak antar garis yang
sejajar selalu sama dan tidak pernah berpotongan. Perhatikan gambar di bawah ini.
Walaupun pada Gambar 4.11 kelihatannya garis-garis tersebut tidak sama panjang,tidak menjadi
alasan untuk menyebut garis-garis tersebut tidak sejajar. Intinya adalah, jika garis tersebut
diperpanjang maka tidak pernah berpotongan, dan terletak pada satu bidang datar, maka garisgaris tersebut merupakan garis-garis sejajar.
b. Menemukan Konsep Sudut
Banyak aktivitas yang kia lakukan dalam kehidupan sehari-hari berkaitan dengan sudut.
Misalnya
pemanah, sudut terbentuk antara tangan dengan badan pemanah. Untuk gambar
pemancing, garis bantu merah sengaja ditambah untuk menunjukkan lebih jelas sudut yang
terbentuk antara pancingan dengan bidang datar.
Sudut terbentuk karena dua sinar bertemu pada titik pangkalnya. Secara matematis, hubungan
sinar garis dan titik sudut diilustrasikan sebagai berikut.
Menentukan besar sudut yang dibentuk oleh jarum jam
Selanjutnya, mari kita cermati pengukuran sudut yang terbentuk oleh jarum jam danjarum menit
pada waktu-waktu yang lain. Perputaran selama 12 jam jarum jam berputar sebesar 360°,
akibatnya pergeseran tiap satu jam adalah
360˚
12
= 30º.
Penamaan sudut
Secara matematis, penamaan sudut diperlukan untuk mempermudah penamaan sudut untuk
kajian selanjutnya. Mari kita perhatikan Gambar 4.17. berikut.
Alat ini dapat membantu kita mengukur suatu sudut yang sudah terbentuk dan membentuk besar
sudut yang akan digambar.
Perlu kita kenalkan bahwa, terdapat ukuran sudut standar yang perlu kita ketahui, seperti yang
disajikan pada gambar di bawah ini.
Dengan memperhatikan ukuran setiap sudut, lengkapilah besar sudut berdasarkan jenis-jenis
sudut.
Memahami Hubungan Antar Sudut
Mari kita perhatikan gambar-gambar berikut ini
Pada Gambar 4.18 terdapat sudut berpelurus, sudut berpenyiku dan sudut bertolak belakang.
Pada kegiatan kali ini kalian akan memperlajari ketiga bentuk hubungan antar sudut tersebut
yang rinciannya dikemas dalam kasus-kasus berikut ini.
a. Sudut Berpelurus dan Sudut Berpenyiku
Hubungan Antar Sudut
1. Sudut Berpenyiku
Dua sudut dikatakan berpenyiku, jika jumlah besar kedua sudut tepat 90˚
2. Sudut Berpelurus
Dua sudut dikatakan berpelurus, jika jumlah besar kedua sudut tepat 180˚
b. Sudut saling betolak belakang
Pada gambar 4.28, <PTR bertolak belakang dengan <STQ, dan <PTS bertolak belakang dengan
<RTQ. Sudut yang saling bertolak belakang mempunyai besar sudut yang sama.
c. Hubungan sudut-sudut pada dua garis sejajar
Sekarang, coba perhatikan kembali gambar lintasan kereta api dan modelnya di bawah
ini.
Garis k dan garis l, dipotong oleh garis garis m pada Gambar 4.29 sehingga membentuk delapan
sudut.
Sudut-sudut ini mempunyai nama khusus sesuai dengan posisinya.