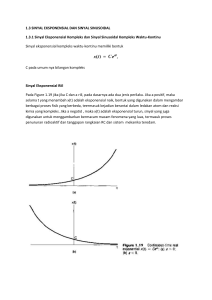
1 BAB I PENDAHULUAN A. Latar Belakang Persamaan

1
BAB I
PENDAHULUAN
A. Latar Belakang
Persamaan eksponensial merupakan salah satu kajian yang menarik
dalam matematika. Persamaan eksponensial adalah persamaan yang
eksponennya mengandung variabel dan tidak menutup kemungkinan bilangan
pokoknya juga mengandung variabel. Variabel adalah simbol (lambang) yang
mewakili sebarang anggota dari suatu himpunan elemen-elemen (Muhsetyo
dkk, 1985). Dari dua definisi di atas dapat diambil beberapa contoh bentukbentuk persamaan eksponensial yaitu, 𝑎𝑎 𝑥𝑥 = 𝑏𝑏, 𝑎𝑎 𝑥𝑥 = 𝑏𝑏 𝑦𝑦 , 𝑥𝑥 𝑥𝑥 = 𝑦𝑦, 𝑥𝑥 𝑦𝑦 = 𝑦𝑦 𝑥𝑥 ,
dimana 𝑎𝑎, 𝑏𝑏 ∈ 𝑹𝑹.
Persamaan eksponensial dapat digunakan untuk menyelesaikan
persoalan dalam kehidupan sehari-hari. Sebagai contoh, untuk menerangkan
peristiwa peluruhan zat radio aktif dalam bidang fisika, untuk menerangkan
peristiwa pertumbuhan bakteri dalam bidang biologi, atau untuk menerangkan
kecepatan bereaksinya dau macam zat dalam ilmu kimia (Margha, 1985).
Solusi dari persamaan eksponensial dapat berupa solusi aljabar.
Namun, untuk kasus-kasus tertentu, solusi dari persamaan eksponensial bisa
juga berupa solusi transcendental. Sebagai contoh adalah persamaan
eksponensial yang berbentuk 𝑥𝑥 𝑦𝑦 = 𝑦𝑦 𝑥𝑥 , 𝑥𝑥 𝑥𝑥 = 𝑦𝑦 𝑦𝑦 , 𝑥𝑥 𝑥𝑥 = 𝑦𝑦, 𝑥𝑥 𝑦𝑦 = 𝑦𝑦 dimana
𝑥𝑥, 𝑦𝑦 > 0, dan 𝑥𝑥 ≠ 𝑦𝑦.
1
Solusi Aljabar dan..., Agus Tuswandi, FKIP UMP, 2012
2
Solusi dari bentuk persamaan eksponensial di atas lebih banyak adalah
berupa bilangan transcendental. Bilangan transcendental adalah bilangan
yang tidak dapat dinyatakan sebagai akar dari suatu polinom dengan koefisien
bilangan rasional (Leithold, 1991).
Solusi aljabar dan transcendental adalah solusi non numerik untuk
persamaan
eksponensial.
Dengan
demikian,
solusi
dari
persamaan
eksponensial yang berbentuk 𝑥𝑥 𝑦𝑦 = 𝑦𝑦 𝑥𝑥 , 𝑥𝑥 𝑥𝑥 = 𝑦𝑦 𝑦𝑦 , 𝑥𝑥 𝑥𝑥 = 𝑦𝑦, 𝑥𝑥 𝑦𝑦 = 𝑦𝑦 dimana
𝑥𝑥, 𝑦𝑦 > 0, dan 𝑥𝑥 ≠ 𝑦𝑦, dapat berupa solusi aljabar dan transcendental.
Dari hal di atas, perlu diteliti bagaimana solusi aljabar dan
transcendental untuk persamaan eksponensial.
B. Rumusan Masalah
Berdasarkan latar belakang di atas, permasalahan yang timbul adalah
bagaimana solusi aljabar dan transcendental untuk persamaan eksponensial.
C. Batasan Masalah
Persamaan eksponensial yang akan dibahas dalam penelitian ini adalah
persamaan eksponensial yang berbentuk 𝑥𝑥 𝑦𝑦 = 𝑦𝑦 𝑥𝑥 , 𝑥𝑥 𝑥𝑥 = 𝑦𝑦 𝑦𝑦 , 𝑥𝑥 𝑥𝑥 = 𝑦𝑦, 𝑥𝑥 𝑦𝑦 = 𝑦𝑦
dimana 𝑥𝑥, 𝑦𝑦 > 0, dan 𝑥𝑥 ≠ 𝑦𝑦.
D. Tujuan Penelitian
Tujuan dalam penelitian ini adalah untuk mengetahui bagaimana solusi
aljabar dan transcendental untuk persamaan eksponensial.
Solusi Aljabar dan..., Agus Tuswandi, FKIP UMP, 2012
3
E. Manfaat Penelitian
Manfaat dari penelitian ini antara lain:
1.
Mendapatkan
tambahan
referensi
tentang
solusi
aljabar
dan
transcendental untuk persamaan eksponensial.
2.
Persamaan
eksponensial
dapat
diaplikasikan
untuk
membantu
menyelesaikan permasalahan dalam bidang kimia.
Solusi Aljabar dan..., Agus Tuswandi, FKIP UMP, 2012