fungsi

MBS - DTA
Sucipto
UNTUK KALANGAN SENDIRI
SMK Muhammadiyah 3 Singosari
SERI : MBS-DTA
FUNGSI
STANDAR KOMPETENSI
Siswa mampu memecahkan masalah yang berkaitan dengan fungsi, persamaan
fungsi linear dan fungsi kuadrat.
KOMPETENSI DASAR
Setelah mempelajari materi ini, siswa diharapkan mampu:
1. Mendeskripsikan perbedaan konsep relasi dan fungsi
2. Menerapkan konsep fungsi linier
3. Menggambarkan fungsi kuadrat
4. Menerapkan konsep fungsi kuadrat
MATERI BELAJAR PRASYARAT
Siswa harus sudah menguasai kompetensi Himpunan dan Sistem Bilangan Real.
1. RELASI DAN FUNGSI
A. Pengertian Relasi dan Fungsi
p
a
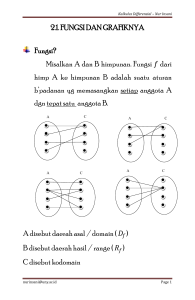
Pada gambar 1 disamping menunjukkan diagram panah
suatu relasi dari himpunan A ke himpunan B, dengan
A = {a, b, c} dan B = {p, q, r, s}. Tampak bahwa setiap
anggota himpunan A dihubungkan dengan tepat pada
satu anggota himpunan B. Relasi yang berciri demikian
disebut dengan fungsi atau pemetaan.
q
b
r
c
s
f
A
Apabila fungsi f memetakan setiap x  A dengan tepat
ke satu anggota y  B, ditulis dengan lambang
f : x  y atau f (x) = y
(dibaca: ”fungsi f memetakan x ke y” atau ”y adalah peta dari x oleh f )
Gambar 1
B
Perhatikan kembali gambar 1.
(i) Daerah asal /domain pada fungsi f tersebut adalah himpunan A = {a, b, c)
(ii) Daerah kawan / kodomain pada fungsi f tersebut adalah himpunan B = {p, q, r, s}
(iii) Daerah hasil / range pada fungsi f tersebut adalah = {p, q, r}
CONTOH 1
Diketahui fungsi f : x  2x + 1 dengan daerah asal D = {x | 1 ≤ x ≤ 3, x  R}
a) carilah nilai fungsi f untuk x = 1, x = 2, dan x = 3 !
b) gambarlah grafik fungsi f pada bidang Cartesius !
c) tentukanlah daerah hasil fungsi f !
b) Grafik fungsi f dinyatakan dengan y = 2x + 1 yaitu
suatu persamaan garis lurus. Beberapa anggota dari f
adalah titik-titik dengan koordinat (1,3), (2,5), dan
(3,7). Titik-titik itu digambar pada bidang Cartesius,
kemudian dihubungkan dengan ruas garis lurus
seperti pada gambar 2.
Y
y = f (x) = 2x + 1
daerah hasil
JAWAB :
f : x  2x + 1, rumus untuk fungsi f adalah f(x) = 2x + 1.
a) Nilai fungsi f :
untuk x = 1 adalah f(1) = 2(1) + 1 = 3
untuk x = 2 adalah f(2) = 2(2) + 1 = 5
untuk x = 3 adalah f(3) = 2(3) + 1 = 7
daerah asal
c) Berdasarkan grafik fungsi f pada gambar 2,
jelas bahwa daerah hasilnya adalah
{y | 3 ≤ y ≤ 7, x  R}.
Gambar 2
B. Jenis-jenis Fungsi
Jenis-jenis fungsi diantaranya adalah sebagai berikut:
1. Fungsi konstan
Fungsi konstan adalah suatu fungsi y = f(x) dengan sama dengan konstanta.
f(x) = k, dengan x  R dan k adalah sebuah konstanta.
X
2. Fungsi identitas
Fungsi identitas adalah fungsi y = f(x) dengan f(x) = x, untuk semua x dalam daerah
asalnya. Fungsi identitas f(x) = x, sering ditulis dengan I(x) = x.
3. Fungsi linier
Fungsi linier adalah fungsi y = f(x) dengan f(x) = ax + b, (dengan a dan b  R, a  0).
Fungsi linier juga dikenal dengan fungsi suku banyak (polinom) berderajat satu.
4. Fungsi kuadrat
Fungsi kuadrat adalah fungsi y = f(x) dengan f(x) = ax2 + bx + c,
dengan a, b dan c  R, a  0.
Fungsi kuadrat juga dikenal dengan fungsi suku banyak (polinom) berderajat dua.
Grafik fungsi kuadrat y = f (x) = ax2 + bx + c, dalam bidang Cartesius dikenal sebagai
parabola.
5. Fungsi modulus atau fungsi nilai mutlak
Fungsi modulus atau fungsi nilai mutlak yaitu fungsi y = f(x) dengan f(x) = | x |
(dibaca: ”nilai mutlak x”) yang didefinisikan sebagai berikut:
 x jika x ≥ 0
Untuk setiap bilangan real x, maka: | x | = 
 –x jika x < 0
CONTOH 2
c) | -4 – 5 | = | -9 | = 9
d) | -3 + 9 | = | 6 | = 6
a) | 5 | = 5
b) | -7 | = 7
Jadi nilai mutlak suatu bilangan real tidak pernah negatif.
6. Fungsi surjektif/fungsi kepada/fungsi onto
Fungsi f : A  B disebut sebagai fungsi surjektif (onto) jika daerah hasil fungsi f sama
dengan himpunan B.
Contoh fungsi surjektif terlihat pada gambar 3.
7. Fungsi injektif/fungsi satu-satu
Fungsi f : A  B disebut sebagai fungsi injektif atau fungsi satu-satu jika dan hanya
jika untuk sembarang a1 dan a2  A dengan a1  a2 berlaku f(a1)  f(a1).
Contoh fungsi injektif terlihat pada gambar 4.
8. Fungsi bijektif
Fungsi f : A  B disebut sebagai fungsi bijektif, jika dan hanya jika fungsi f adalah
fungsi surjektif dan juga fungsi injektif.
Contoh fungsi injektif terlihat pada gambar 4.
1
2
3
4
f
x
y
z
B
A
Gambar 3
1
2
3
f
x
y
z
B
A
Gambar 4
LATIHAN 1
1. Sebutkan relasi-relasi pada gambar di bawah ini, manakah yang merupakan fungsi ?
a.
a
b
c
d
b.
p
q
r
d.
a
b
c
d
c.
p
q
r
e.
a
b
c
d
p
q
r
a
b
c
d
p
q
r
a
b
c
d
p
q
r
f.
a
b
c
d
p
q
r
2. Daerah asal fungsi f : x  x – 3 adalah D = {x | 0 ≤ x ≤ 4, x  R}.
a. tentukan nilai fungsi f untuk x = 0, x = 1, x = 2, x = 3 dan x = 4.
b. gambarlah grafik fungsi f pada bidang Cartesius.
c. tentukan daerah hasil fungsi f.
3. Diketahui fungsi f : x  (ax + b) dengan a dan b  B. Jika f (1) = 1 dan f (2) = -1,
a. carilah nilia a dan b.
b. hitunglah nilai-nilai f (-2), f (-1), f (0), f (3) dan f (4).
c. gambarlah grafik fungsi f pada bidang Cartesius.
4. Diketahui fungsi f : x  (x2 – 3x + 2) dengan daerah asal D = {-2, -1, 0, 1, 2}. Tentukan
daerah hasilnya !
2. FUNGSI LINIER
A. Menggambar Grafik Fungsi Linier
Bentuk umum fungsi linier adalah sebagai berikut:
f (x) = ax + b dengan a dan b  R, a  0.
Grafik fungsi linier y = ax + b dalam bidang Cartesius berupa garis lurus. Grafik fungsi
linier memotong sumbu Y di sebuah titik dengan ordinat y = b. Bilangan a disebut gradien
atau koefisien arah dari garis lurus tersebut, dan a = tan  dengan  adalah sudut yang
dibentuk garis lurus dengan sumbu X positif.
CONTOH 3
Diketahui fungsi linier dengan rumus f(x) = ax + b dengan nilai f (0) = 4 dan nilai f (4) = -4.
a. Hitunglah nilai a dan b, kemudian tulislah rumus untuk fungsi f (x).
b. Tentukan titik-titik potong fungsi f dengan sumbu X maupun sumbu Y.
c. Gambarlah grafik fungsi f pada bidang Cartesius untuk daerah asal D = {x | x  R}
JAWAB :
a. f (x) = ax + b, untuk f (0) = 4 diperoleh a(0) + b = 4 (x pada ax + b diganti dengan 0)
b=4
untuk f (4) = -4 diperoleh a(4) + 4 = -4 (x diganti 4, dan b diganti 4)
4a + 4 = -4
4a = -8
a = -2
 Jadi rumus untuk fungsi f (x) dengan a = -2 dan b = 4 adalah f (x) = -2x + 4
b. Untuk rumus fungsi f (x) = -2x + 4 maka
persamaan grafik fungsinya adalah y = -2x + 4
Y
 Titik potong grafik dengan sumbu X
diperoleh jika y = 0, sehingga
-2x + 4 = 0
-2x = -4
x =2
Jadi titik potong grafik dengan sumbu X
di titik (2,0).
 Titik potong grafik dengan sumbu Y
diperoleh jika x = 0, sehingga
y = -2(0) + 4
y=4
Jadi titik potong grafik dengan sumbu Y
di titik (0, 4).
c. Grafik fungsi y = -2x + 4 untuk x  R pada
bidang Cartesius diperlihatkan pada gambar 5
6
5
4
(0,4)
3
y = -2x + 4
2
1
-1
0
(2,0)
1
2
3
4
5
6
X
-1
-2
-3
Gambar 5
LATIHAN 2
1. Diketahui fungsi linier f : x  f (x) = ax + b dengan nilai f (-1) = 4 dan nilai f (2) = -2
a. Hitunglah nilai a dan b, kemudian tulislah rumus untuk fungsi f (x).
b. Tentukan titik-titik potong fungsi f dengan sumbu X maupun sumbu Y.
c. Gambarlah grafik fungsi f pada bidang Cartesius untuk daerah asal D = {x | x  R}
2. Diketahui fungsi linier f : x  f (x) = ax + b dengan nilai f (1) = -2 dan nilai f (3) = 2
a. Hitunglah nilai a dan b, kemudian tulislah rumus untuk fungsi f (x).
b. Tentukan titik-titik potong fungsi f dengan sumbu X maupun sumbu Y.
c. Gambarlah grafik fungsi f pada bidang Cartesius untuk daerah asal D = {x | x  R}
3. Diketahui fungsi linier dengan rumus fungsi f (x) = 2x – 4.
a. Tentukan titik-titik potong fungsi f dengan sumbu X maupun sumbu Y.
b. Gambarlah grafik fungsi f pada bidang Cartesius untuk daerah asal D = {x | x  R}
4. Gambarlah grafik fungsi f pada bidang Cartesius untuk daerah asal D = {x | x  R} jika
diketahui fungsi f (x) = 3 – x
B. Menentukan Persamaan Grafik Fungsi Linier
B.1. Persamaan Garis Lurus Jika Melalui Sebuah Titik Dengan Gradien Tertentu
Seperti disebutkan pada awal bab ini, pada persamaan fungsi linier y = ax + b,
a merupakan gradien dari grafik fungsi tersebut. Untuk selanjutnya istilah gradien
garis lurus dilambangkan dengan m, sehingga persamaannya menjadi y = mx + b.
Sebagai contoh, jika persamaan garis y = 3x + 5 mempunyai gradien 3, sedangkan
persamaan garis y   x  5 mempunyai gradien  1 .
Untuk menyusun persamaan garis lurus yang melalui sebuah titik (x1, y1) dengan
gradien m dapat menggunakan rumus sebagai berikut:
y – y1 = m(x – x1)
...... ( 1 )
CONTOH 4
Sebuah grafik fungsi linier mempunyai gradien 2 dan melalui sebuah titik dengan
koordinat (3,2). Tentukan persamaan grafik fungsi tersebut !
JAWAB :
Diketahui:
- titik koordinat yang dilalui grafik adalah (3,2) maka x1 = 3 dan y1 = 2
- gradien garis m = 2 sehingga
y – y1 = m(x – x1)
y – 2 = 2(x – 3)
y – 2 = 2x – 6
y = 2x – 6 + 2
y = 2x – 4
( y1 diganti 2, m diganti 2, dan x1 diganti 3)
Jadi, persamaan garis yang melalui titik (3,2) dengan gradien 2 adalah y = 2x – 4
B.2. Persamaan Garis Lurus Jika Melalui Dua Titik
Untuk menentukan gradien (m) dari sebuah garis yang melalui titik A(x1, y1) dan titik
B(x2, y2), dapat menggunakan rumus berikut ini.
m
y 2  y1
x 2  x1
.... ( 2 )
Sedangkan untuk menyusun sebuah persamaan garis yang melalui titik A(x1, y1) dan
titik B(x2, y2), dapat menggunakan rumus berikut ini.
y  y1
x  x1

y 2  y1 x 2  x1
.... ( 3 )
atau dapat juga menggunakan rumus y – y1 = m(x – x1), setelah gradien m dicari
terlebih dahulu menggunakan rumus (2) diatas.
CONTOH 5
Sebuah grafik garis lurus melalui titik A(-1,2) dan titik B(3,-2). Susunlah persamaan
grafik fungsi tersebut!
JAWAB :
>> titik A(-1,2)  sehingga x1 = -1, dan y1 = 2
>> titik B(3,-2)  sehingga x2 = 3, dan y2 = -2
y  y1
x  x1

y 2  y1 x 2  x1
y2
x  (1)

 2  2 3  (1)
y  2 x 1

4
4
(dengan perkalian silang diperoleh ...)
4( y  2)  4( x  1)
4 y  8  4 x  4
4 y  4 x  4  8
4 y  4 x  4
(kedua ruas dikali dengan ¼ sehingga menjadi …)
y  x 1
B.3. Persamaan Garis Lurus Jika Diketahui Grafiknya
Y
CONTOH 6
Sebuah grafik fungsi linier tampak seperti pada
gambar 6. Tentukan persamaan dari grafik
fungsi disamping !
4
3
2
1
-1
0
1
2
3
-1
-2
4
5
X
JAWAB :
Cara menyelesaikan permasalahan di atas, sama
dengan mencari persamaan grafik yang melalui
dua titik.
Pada gambar 6 terlihat bahwa titik yang dilalui
grafik adalah (2,0) dan (0,-4).
-3
-4
BISAKAH ANDA MELANJUTKAN ?
-5
PASTI ..... BISA .... !!!
Gambar 6
atau dapat juga menggunakan rumus :
x
x
dengan
'

y
y'
1
...... ( 4 )
x ' = nilai x yang dipotong grafik pada sumbu X, dan
y ' = nilai y yang dipotong grafik pada sumbu Y
C. Dua Garis Lurus Yang Saling Sejajar
Perhatikan gambar 7 di samping.
Garis f dan g dikatakan saling sejajar jika
gradien f sama dengan gradien g.
Y
6
5
Jika f sebagai grafik fungsi ke-1 dan
g sebagai grafik fungsi ke-2, maka dapat
dituliskan syarat dua buah garis dikatakan
saling sejajar jika:
4
3
2
m1 = m2
...... ( 5 )
1
-1
0
1
2
3
4
5
6
X
Persamaan garis f adalah y   32 x  3
-1
maka gradien f adalah mf = 
-2
3
2
g
f
-3
Persamaan garis g adalah y   32 x  6
maka gradien g adalah mg = 
3
2
Gambar 7
Dari penjelasan di atas dapat dibuat sebuah kesimpulan, bahwa karena mf = mg = 
3
2
maka
garis f dan g saling sejajar.
D. Dua Garis Lurus Yang Saling Tegak Lurus
Perhatikan gambar 8 di samping.
Garis f dan g dikatakan saling tegak lurus
jika hasil kali antara gradien f dengan
gradien g sama dengan  1 .
Y
6
5
Jika f sebagai grafik fungsi ke-1 dan
g sebagai grafik fungsi ke-2, maka dapat
dituliskan syarat dua buah garis dikatakan
saling tegak lurus jika:
m1  m2  1
g
4
3
2
...... ( 6 )
1
-1
0
Persamaan garis f adalah y  2 x  4
maka gradien f adalah mf =  2
-1
Persamaan garis g adalah y  12 x  3
-3
maka gradien g adalah mg =  12
-2
1
2
3
4
5
6
X
f
Gambar 8
Dari penjelasan di atas dapat dibuat sebuah kesimpulan, bahwa karena mf . mg =  1 maka
garis f dan g saling tegak lurus.
CONTOH 6
Diketahui garis k dengan persamaan y  2 x  4 .
a. tentukan persamaan garis f yang sejajar dengan garis k dan melalui titik (2,4)
b. tentukan persamaan garis g yang tegak lurus dengan garis k dan melalui titik (4.3)
JAWAB :
a. - Langkah (i) mencari m1 (gradien garis k),
garis k mempunyai persamaan y  2 x  4 sehingga m1 =  2
- Langkah (ii) mencari m2 (gradien garis f )
karena garis f sejajar dengan k ( f // k ), maka m2 = m1 =  2
- Langkah (iii) mencari persamaan garis f dengan m2 =  2 dan melalui titik (2,4)
dari titik (2,4) dapat ditentukan x1 = 2 dan y1 = 4, sehingga ...
y  y1  m( x  x1 )
y  4  2( x  2)
( ingat ..., yang dimasukkan adalah m2 )
y  2 x  4  4
y  2 x  8
Jadi persamaan garis f yang sejajar garis k dan melalui titik (2,4) adalah y  2 x  8 .
b. - Langkah (i) mencari m1 (gradien garis k),
garis k mempunyai persamaan y  2 x  4 sehingga m1 =  2
- Langkah (ii) mencari m2 (gradien garis g)
karena garis g tegak lurus dengan k ( g  k), maka
m1  m2  1
 2  m2  1
m2  12
- Langkah (iii) mencari persamaan garis g dengan m2 =
1
2
dan melalui titik (4,3)
dari titik (4,3) dapat ditentukan x1 = 4 dan y1 = 3, sehingga ...
y  y1  m( x  x1 )
y  3  12 ( x  4)
( ingat ..., yang dimasukkan adalah m2 )
y  12 x  2  3
y  12 x  1
( atau jika kedua ruas dikali dengan 2 )
2 y  x  2 atau dapat ditulis menjadi 2 y  x  2
Jadi persamaan garis g yang tegak lurus denga garis k dan melalui titik (4,3) adalah
y  12 x  1 .
LATIHAN 3
1. Tentukanlah gradien dari masing-masing persamaan grafik fungsi di bawah ini:
a. y  5x  20
d. 2 y  x  5
b. y  3x  6
e. 3 y  6 x  10
c. y  8  4 x
f. 2 x  3 y  12
2. Tentukan gradien dari masing-masing persamaan grafik fungsi linier di bawah ini jika
melalui titik-titik koordinat yang dimaksud:
a. titik (2, 4) dan (3, 0)
d. titik A(–2, –4) dan B(3, 6)
b. titik (3, 0) dan (0, 6)
e. titik P(1, –3) dan Q(–5,6)
c. titik (–3, 2) dan (2, –3)
f. titik K(–3, 5) dan O(0, 0)
3. Susunlah persamaan grafik fungsi linier yang melalui sebuah titik dan gradien berikut ini:
a. melalui (2, 2) dengan m = –1
c. melalui (3, –2) dengan m = –2
b. melalui (2, 4) dengan m = ½
d. melalui (–3, –2) dengan m = 2/3
4. Susunlah persamaan grafik fungsi yang melalui titik pusat dan titik:
a. (4, –3)
b. (–2, 5)
5. Susunlah persamaan grafik fungsi yang melalui titik-titik berikut ini:
a. (4, 3) dan (1, –1)
b. (2, 5) dan (3, 0)
6. Tentukan persamaan garis dari grafik fungsi di bawah ini:
a.
b.
Y
Y
4
7
3
6
2
5
1
4
-2
-1
-2
-1
0
3
-1
2
-2
1
-3
0
1
2
3
4
5
X
1
2
3
4
-4
-1
-5
-2
-6
-3
7. Diketahui garis g dengan persamaan 2 y  4 x  5 . Tentukan persamaan garis p yang
melalui (4,-2) jika garis p // g.
8. Tentukan persamaan grafik fungsi h yang tegak lurus dengan garis k : y  34 x  2 dan
melalui titik (-2, 5).
5
X
E. Invers Fungsi Linier
Jika hasil pemetaan fungsi y = f(x) dipetakan lagi oleh pemetaan g hasilnya kembali ke titik
semula yaitu x, g(f(x)) = x maka g dikatakan invers dari f. Salah satu ide menentukan
invers y = f(x) adalah mengubah x sebagai fungsi dari y, yaitu x = g(y).
Kadang-kadang proses seperti itu merupakan proses yang mudah atau ada kalanya cukup
rumit. Namun untuk fungsi linear, proses mengubah y = f(x) menjadi x = g(y) cukuplah
sederhana. Sebagai contoh perhatikanlah contoh berikut ini:
CONTOH 7
Tentukanlah invers dari fungsi linier y  5x  2
JAWAB :
y  5x  2
 dapat ditulis sebagai y  f (x)
( y dalam bentuk fungsi x )
Sekarang tinggal mengubah x ke dalam fungsi y.
 5x   y  2
x
 y2
5
x  15 y  52 atau
x  15 ( y  2)  dapat ditulis sebagai x  g ( y)
( x dalam bentuk fungsi y )
Dari persamaan di atas, jika x diganti dengan y dan y diganti dengan x maka diperoleh
fungsi y = g(x) dengan persamaan:
y  15 ( x  2)
 ini adalah invers dari fungsi y  5x  2
Proses yang demikian ini merupakan proses menentukan fungsi invers.
Jadi y = g(x) invers dari y = f(x) dan y = f(x) invers dari y = g(x).
LATIHAN 4
1. Tentukanlah invers dari fungsi linier dengan persamaan sebagai berikut:
a. y  5x  20
b.
y  23 x  6
c.
y  8  4x
2. Jika g(x) adalah invers dari f(x), tentukanlah fungsi g(x) jika:
a. f ( x)  2 x  10
b. f ( x)  4 x  6
c.
f ( x)  12 x  8
3. FUNGSI KUADRAT
A. Pengertian Fungsi Kuadrat
Fungsi kuadrat adalah fungsi y = f(x) dengan f(x) = ax2 + bx + c, ( a, b dan c  R, a  0).
Fungsi kuadrat juga dikenal dengan fungsi suku banyak (polinom) berderajat dua.
Persamaan grafik fungsi kuadrat adalah y = ax2 + bx + c, (a  0) dalam bidang Cartesius
dikenal sebagai parabola.
B. Sifat-sifat Grafik Fungsi Kuadrat
Sifat-sifat grafik fungsi kuadrat f(x) = ax2 + bx + c adalah:
1. Berdasarkan nilai a
a) Jika a > 0 (a positif), maka grafik terbuka ke atas.
b) Jika a < 0 (a negatif), maka grafik terbuka ke bawah.
2. Berdasarkan nilai diskriminan
Nilai diskriminan suatu persamaan kuadrat dinyatakan dengan D = b2 – 4ac. Sifat-sifat
dari persamaan fungsi kuadrat berdasarkan nilai diskriminannya adalah sebagai
berikut:
a) Jika D > 0, maka grafik memotong sumbu X di dua titik yang berbeda (x1  x2)
b) Jika D = 0, maka grafik menyinggung sumbu X di satu titik (x1 = x2)
c) Jika D < 0, maka grafik tidak memotong sumbu X.
C. Langkah-langkah Menggambar Grafik Fungsi Kuadrat
Langkah-langkah menggambar grafik fungsi kuadrat f(x) = ax2 + bx + c pada bidang
Cartesius adalah sebagai berikut:
1. Menentukan titik potong dengan sumbu X (sama artinya dengan jika y = 0)
2. Menentukan titik potong dengan sumbu Y (sama artinya dengan jika x = 0)
3. Menentukan persamaan sumbu simetri
b
Persamaan sumbu simetri dapat dicari dengan rumus : x 
...... ( 7 )
 2a
4. Menentukan koordinat titik balik (titik ekstrem atau titik puncak)
Titik balik yang dimaksud adalah koordinat (x, y) dengan nilai x dan y yang dapat
dicari dengan rumus:
x
b
 2a
dan
y
D
 4a
dengan D  b 2  4ac
CONTOH 8
Diketahui fungsi kuadrat f ( x)  x 2  3x  4 . Buatlah grafik parabolanya!
JAWAB :
f ( x)  x 2  3x  4 maka persamaan fungsinya adalah y  x 2  3x  4
(1) Menentukan titik potong dengan sumbu X, jika y = 0
0  x 2  3x  4 atau dapat ditulis
x 2  3x  4  0
( x  4)(x  1)  0
x  4  0 atau x  1  0
x=4
x = 1
Jadi, titik potong dengan sumbu X pada titik (4, 0) dan (–1, 0).
...... ( 8 )
(2) Menentukan titik potong dengan sumbu Y, jika x = 0
y  x 2  3x  4
y  0 2  3(0)  4
y  4
Jadi, titik potong dengan sumbu Y pada titik (0, –4).
(3) Menentukan persamaan sumbu simetri
Dari persamaan y  x 2  3x  4 diketahui a = 1, b = –3, dan c = –4, sehingga
b
3
3
1
Garis ini adalah sumbu
x

 1
 2a  2(1) 2
2
simetri dengan
Y
persamaan
1
x = 1½
Jadi, persamaan sumbu simetrinya x  1
4
2
(4) Menentukan koordinat titik balik fungsi.
Untuk nilai x sama dengan nilai x pada
1
persamaan sumbu simetri, yaitu x  1
2
Sedangkan untuk mencari nilai y menggunakan
D
b 2  4ac
rumus: y 

 4a
 4a
2
(3)  4.1.(4) 9  16 25
1
y


 6
 4.(1)
4
4
4
Jadi, koordinat titik baliknya
( 1 12
,  6 14
).
Sehingga gambar grafik fungsi kuadrat
f ( x)  x 2  3x  4 dapat dilihat pada gambar 9.
3
2
1
-2
-1
0
1
2
3
4
5
-1
-2
-3
-4
-5
-6
-7
Gambar 9
CONTOH 9
Tentukan nilai k supaya grafik fungsi kuadrat f ( x)  (1  k 2 ) x 2  10kx  16 menyinggung
sumbu X !
JAWAB :
Dari rumus fungsi diketahui a = (1 + k2), b = 10k, dan c = 16
Grafik fungsi kuadrat dikatakan menyinggung sumbu X, jika D = 0, sehingga ...
D = 0
b2 – 4ac = 0
(10k)2 – 4.(1 + k2).16 = 0
100k2 – 64.(1 + k2) = 0
100k2 – 64 – 64k2 = 0
36k2 – 64 = 0
(6k – 8) (6k + 8) = 0
6k – 8 = 0
atau 6k + 8 = 0
6k = 8
6k = –8
k=
8 4

6 3
k= 
8
4

6
3
Jadi, agar grafik fungsi kuadrat menyinggung sumbu X, maka nilai k adalah
4
4
atau  .
3
3
X
LATIHAN 5
1. Tentukanlah sifat-sifat grafik fungsi kuadrat berikut berdasarkan nilai a dan
diskriminannya !
y  ( x  4) 2
a.
y  x 2  12x  20
d.
b.
y   x 2  4 x  10
e. y  6 x 2  9 x
c. y  2 x 2  x  1
2. Buatlah gambar grafik fungsi kuadrat jika :
a.
f ( x)  x 2  3 x  4
c. y  x 2  6 x
b. g ( x)  x 2  4
d. y   x 2  4 x  12
3. Tentukan nilai k supaya grafik fungsi kuadrat berikut menyinggung sumbu X !
a. y = kx2 + 6x + 9
b. y = x2 – 2kx + (3k + 4)
D. Menyusun Persamaan Grafik Fungsi Kuadrat
Persamaan grafik fungsi kuadrat dapat dicari dengan beberapa cara, diantara adalah:
1. Jika grafik fungsi kuadrat melalui titik (x, y) dengan titik puncak (p, q) dapat
ditentukan dengan menggunakan rumus:
y  a( x  p) 2  q
..... ( 9 )
2. Jika grafik fungsi kuadrat memotong sumbu X di titik (x1, 0) dan (x2, 0) serta melalui
titik sembarang (x, y) dapat ditentukan dengan menggunakan rumus:
y  a( x  x1 )(x  x2 )
..... ( 10 )
CONTOH 10
Tentukan persamaan grafik fungsi kuadrat yang mempunyai titik balik (1, –1) serta melalui
titik (2, 3) !
JAWAB :
( i ) Langkah pertama adalah mencari nilai a.
Karena titik balik grafik adalah (1, –1) maka p = 1 dan q = –1, dan titik yang dilalui
(2, 3) sehingga persamaannya adalah:
y  a( x  p) 2  q
3 = a(2 – 1)2 + (–1)
3 = a.1 – 1
a=4
( ii ) Langkah kedua mencari persamaan grafik fungsi kuadrat yang dimaksud.
Dengan a = 4 dengan titik balik (1, –1) maka persamaannya adalah:
y = 4(x – 1)2 + (–1)
y = 4(x2 – 2x + 1) – 1
y = 4x2 – 8x + 4 – 1
y = 4x2 – 8x + 3
Jadi, persamaan grafik fungsi kuadrat dengan titik balik (1, –1) serta melalui titik (2, 3)
adalah y = 4x2 – 8x + 3.
CONTOH 11
Tentukan persamaan grafik fungsi kuadrat yang memotong sumbu X di titik (–2, 0) dan
(3, 0) serta melalui titik (1, 6) !
JAWAB :
Grafik memotong sumbu x di titik (–2, 0) dan (3, 0) sehingga persamaannya menjadi
y  a( x  2)(x  3)
dengan melalui titik (1, 6) maka ...
6  a (1  2)(1  3)
6  a.(3).(2)
6  6a
a  1
Dengan mensubstitusikan a = –1 ke persamaan y  a( x  2)(x  3) didapat
y  1( x  2)(x  3) =  1( x 2  x  6)
y  x 2  x  6
Jadi, persamaan grafik fungsinya adalah y   x 2  x  6 .
LATIHAN 6
1. Tentukanlah persamaan grafik fungsi kuadrat berikut jika:
a. Grafik melalui titik (0, 8) dengan titik puncak (3, 1)
b. Grafik mempunyai titik puncak di P(2, 1) serta melalui titik (3, 1)
2. Tentukanlah persamaan grafik fungsi kuadrat berikut jika:
a. Grafik memotong sumbu X di titik (-1, 0) dan (1, 0) serta melalui titik (2, 1)
b. Grafik memotong sumbu X di titik (-3, 0) dan (1, 0) serta melalui titik (0, 9)
3. Tentukan fungsi kuadrat jika grafiknya mempunyai titik balik ( P(3, -1) serta f(1) = 7
4. Tentukan fungsi kuadrat yang mempunyai pembuat nol fungsi 2 dan 6 sedangkan nilai
maksimumnya adalah 9.