RENCANA PELAKSANAAN PEMBELAJARAN (RPP) Satuan

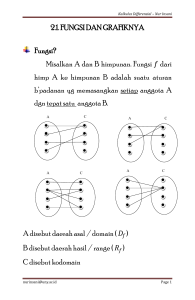
RENCANA PELAKSANAAN PEMBELAJARAN
(RPP)
I.
Satuan Pendidikan
: SMA Negeri 1 Sukasada
Mata Pelajaran
: Matematika
Kelas/Semester
: X/1 (Ganjil)
Alokasi waktu
: 2 x 45 menit (1 pertemuan)
Standar Kompetensi
1.1 Memecahkan masalah yang berkaitan dengan fungsi, persamaan, dan fungsi kuadrat
serta pertidaksamaan kuadrat.
II. Kompetensi Dasar
2.1 Menggambar grafik fungsi aljabar sederhana (fungsi linear) dan fungsi kuadrat.
III. Indikator
3.1 Menentukan domain fungsi linear.
3.2 Menentukan daerah hasil (range) fungsi linear.
3.3 Menentukan titik-titik potong grafik fungsi linear dengan sumbu koordinat yaitu sumbu
dan sumbu .
3.4 Menggambarkan grafik fungsi linear.
3.5 Menentukan titik-titik potong grafik fungsi kuadrat dengan sumbu koordinat yaitu
sumbu
dan sumbu .
3.6 Menentukan koordinat titik puncak grafik fungsi kuadrat.
3.7 Menentukan persamaan sumbu simetri grafik fungsi kuadrat.
3.8 Menggambarkan grafik fungsi kuadrat.
IV. Tujuan Pembelajaran
Melalui pembelajaran kooperatif (tipe STAD), berbantuan LKS, diskusi dan tanya jawab,
diharapkan tercapai tujuan pembelajaran sebagai berikut;
4.1 siswa mampu menentukan domain fungsi linear.
4.2 siswa mampu menentukan daerah hasil (range) fungsi linear.
4.3 siswa mampu menentukan titik-titik potong grafik fungsi linear dengan sumbu
koordinat yaitu sumbu
dan sumbu .
4.4 siswa mampu menggambarkan grafik fungsi linear.
4.5 siswa mampu menentukan titik-titik potong grafik fungsi kuadrat dengan sumbu
koordinat yaitu sumbu
dan sumbu .
4.6 siswa mampu menentukan koordinat titik puncak grafik fungsi kuadrat.
4.7 siswa mampu menentukan persamaan sumbu simetri grafik fungsi kuadrat.
4.8 siswa mampu menggambarkan grafik fungsi kuadrat.
Karakter yang diharapkan dapat muncul pada siswa dalam proses pembelajaran:
a. rasa ingin tahu, diantaranya siswa ikut berpartisipasi aktif dalam proses
pembelajaran, mengajukan pertanyaan dan memberikan pendapat.
b. kerja keras, diantaranya dalam menggambarkan grafik fungsi aljabar linear
sederhana (fungsi linear) dan fungsi kuadrat.
c. teliti, diantaranya melalui melalui mengerjakan soal-soal sehingga mendapatkan
hasil yang sesuai dan tepat.
V. Sumber dan Alat Pembelajaran
Sumber Pembelajaran
1.
Buku penunjang sesuai dengan materi yaitu buku Cerdas Belajar Matematika kelas X .
2.
Buku Matematika SMA (LKS Terstruktur) Kelas X, Semester I oleh MGMP yang
sesuai dengan materi menggambarkan fungsi linear dan fungsi kuadrat dan diterbitkan
UD.Laksamana.
3.
Buku referensi lain.
Alat Pembelajaran
1.
Papan Tulis
2.
Spidol
VI. Materi Ajar
A. Menggambar Grafik Fungsi Aljabar Sederhana (Fungsi Linear)
Fungsi aljabar adalah fungsi yang menggunakan operasi-operasi penjumlahan,
pengurangan, perkalian, pembagian, perpangkatan, dan penarikan akar. Salah satu bentuk
fungsi aljabar yang sederhana adalah fungsi linear. Bentuk umum fungsi linear adalah
dengan a, b
,
. Kurva fungsi linear berupa garis
yang selalu melalui titik
dan
fungsi linear dengan sumbu
Titik
sedangkan
merupakan titik potong grafik
merupakan titik potong dengan sumbu
.
Berikut langkah-langkah menggambarkan grafik fungsi linear beserta contoh:
Misalkan diketahui fungsi
. Tentukan titik potong grafik
fungsi dengan sumbu X dan sumbu Y, domain, range dan gambarkan grafik fungsi linear
tersebut.
1) Suatu grafik memotong sumbu X jika dipenuhi syarat
. Titik potong dengan sumbu X,
atau
(
Suatu grafik memotong
sumbu Y jika dipenuhi syarat
. Titik potong dengan
sumbu Y, (
2) Domain fungsi adalah nilai
ditentukan
yang memenuhi fungsi tersebut. Karena sudah
, maka domain fungsi f adalah
.
3) Daerah hasil (range) fungsi, dapat dicari dengan mengambil sampel beberapa titik
atau nilai
pada domain kemudian mensubstitusikannya ke dalam fungsi.
-5
-4
-3
-2
-1
0
1
2
3
-11
-9
-7
-5
-3
-1
1
3
5
4) Gambar grafik fungsi,
B. Fungsi Kuadrat
Fungsi kuadrat adalah suatu fungsi
dengan
pada himpunan bilangan riil
dengan
dan
yang dirumuskan
.
B.1 Menggambar Sketsa Grafik Fungsi Kuadrat.
Berikut ini adalah langkah-langkah untuk melukis grafik fungsi kuadrat
1) Menentukan Titik-Titik Potong dengan Sumbu Koordinat.
a) Titik potong grafik dengan sumbu X. Suatu grafik memotong sumbu X jika
dipenuhi syarat
atau
. Banyaknya akar real
dari sebuah persamaan kuadrat ditentukan oleh tanda diskriminan
.
, grafik
memotong sumbu X di dua titik,
.
, grafik
memotong sumbu X di satu titik,
, grafik
tidak memotong sumbu X.
Titik potong grafik dengan sumbu
dipenuhi syarat
Suatu grafik memotong sumbu Y jika
.
Jadi, titik potong dengan sumbu
.
adalah
b) Menentukan Titik Puncak Grafik Fungsi Kuadrat.
Untuk menentukan titik puncak kita dapat mengubah fungsi kuadrat menjadi
bentuk kuadrat sempurna.
Dari bentuk kuadrat sempurna tersebut diperoleh bahwa nilai
tidak akan pernah negatif berapa pun nilai
maksimum/minimum untuk
. Sehingga nilai fungsi akan
atau
dan nilai ekstrim atau
maksimum/minimum fungsi adalah
Jika nilai
grafik fungsi kuadrat yang berupa parabola terbuka ke
atas. Jenis titik ekstrimnya adalah titik minimum dan jenis nilai
ekstrimnya adalah nilai minimum (diberi lambang
Jika nilai
.
grafik fungsi kuadrat yang berupa parabola terbuka ke
bawah. Jenis titik ekstrimnya adalah titik maksimum dan jenis nilai
ekstrimnya adalah nilai maksimum (diberi lambang
Jadi, koordinat titik puncak/titik ekstrim dari fungsi kuadrat adalah
.
.
c) Menentukan Sumbu Simetri Grafik Fungsi Kuadrat.
Ada dua kemungkinan grafik fungsi kuadrat seperti pada gambar di bawah ini.
sumbu simetri
sumbu simetri
titik maksimum
titik minimum
Parabola terbuka ke atas
Parabola terbuka ke bawah
Sumbu simetri grafik fungsi kuadrat adalah garis yang melalui titik puncak
dan sejajar dengan sumbu . Berdasarkan pengertian sumbu simetri di atas, jadi
persamaan sumbu simetri fungsi kuadrat, f(x) = ax2 + bx + c adalah:
C. Menggambar grafik fungsi kuadrat
Adapun langkah-langkah menggambar grafik fungsi kuadrat f(x) = ax2 + bx + c yaitu
sebagai berikut.
1. Tentukan titik potong
dengan sumbu X.
2. Tentukan titik potong
dengan sumbu Y.
3. Tentukan koordinat titik puncaknya
4. Tentukan persamaan sumbu simetrinya.
5. Gambar grafik fungsi kuadrat.
Contoh:
Gambarlah
=
Penyelesaian:
1. Titik potong f(x) dengan sumbu X
f(x) = 0
f(x) = x2 – 4x + 3 = 0
(x – 3)(x – 1) = 0
x = 3 atau x = 1
Jadi, titik potongnya adalah (3, 0) dan (1, 0).
2. Titik potong f(x) dengan sumbu Y
f(x) = x2 – 4x + 3
f(0) = 0 – 0 + 3
f(0) = 3
Jadi, titik potongnya adalah (3, 0)
3. Persamaan sumbu simetri
Jadi, sumbu simetrinya x = 2
4. Titik puncaknya
Jadi, titik puncaknya (2, -1)
-8
y
f(x)=x^2-4*x
13
12
Gambarnya sebagai berikut.
11
10
9
f (x) = x2 - 4x + 3
8
7
6
5
4
3
2
1
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
7
8
9
10
11
-1
-2
-3
-4
-5
-6
VII. Model dan Metode Pembelajaran
-7
-8
1. Model Pembelajaran yang
digunakan adalah model pembelajaran kooperatif (Cooperatif
Learning) tipe STAD. -9
2. Metode Pembelajaran-10
yang digunakan adalah diskusi, tanya jawab, dan pemberian tugas.
-11
-12
-13
12
13
VIII. Langkah-langkah Kegiatan Pembelajaran
Struktur
Aktivitas Guru
Pendahuluan
APERSEPSI
Alokasi
AktivitasSiswa
o Menyampaikan tujuan
waktu
o Siswa mendengarkan dan
pembelajaran yang ingin dicapai
mencermati tujuan
dalam kegiatan pembelajaran.
pembelajaran yang
5 menit
disampaikan oleh guru.
o Guru
mengingatkan
kembali o Mendengarkan dan
siswa mengenai bentuk umum
mencermati penjelasan
fungsi linear, bentuk umum
guru
fungsi kuadrat, cara mencari
nilai suatu fungsi dan akar-akar
persamaan kuadrat.
MOTIVASI
o Guru memberikan acuan materi o Mendengarkan
berupa penjelasan pokok dan
mencermati
uraian materi pelajaran secara
guru.
dan 20 menit
penjelasan
garis besar.
Inti
o Mengintruksikan
siswa
untuk o Duduk
duduk berdasarkan kelompoknya.
berdasarkan 15 menit
kelompoknya.
(agar kemampuan siswa di setiap
kelompok rata, guru membantu
membentuk kelompok)
(dalam kelompok)
EKSPLORASI
o Memberikan
LKS
kepada
o Mencermati
LKS
yang
masing-masing kelompok yang
diberikan.
sudah dibentuk dan meminta
siswa untuk mencermati LKS.
o Jika ada siswa atau kelompok
o Menanyakan pada guru
yang belum mengerti instruksi
jika ada instruksi pada
dari LKS, guru menjelaskan
LKS
instruksi tersebut pada siswa.
dipahami.
yang
belum
ELABORASI
o Membantu
mengalami
kesulitan
mengerjakan LKS
penerapan
yang o Menanyakan
siswa
dalam
dan soal
dengan
masalah
masalah- 30 menit
yang
ditemui
kepada teman yang sudah
cara
paham ataupun guru dalam
memberikan pertanyaan arahan
mengerjakan LKS dan soal
sehingga siswa sendiri yang
penerapan.
berhasil memecahkan masalah
tersebut.
o Menunjuk
perwakilan
acak o Mempresentasikan
secara
kelompok
hasil
untuk
diskusi kelompok di depan
mempresentasikan hasil kerja
kelas (bagi siswa yang
kelompoknya di depan kelas.
ditunjuk) dan mencermati
pekerjaan
siswa
yang
ditunujk di depan kelas.
KONFIRMASI
o Memberikan
pelurusan o Mendengarkan dengan baik 5 menit
mengenai hasil diskusi siswa.
penjelasan guru.
o Kelompok yang paling aktif
diberikan penguatan oleh guru.
o Mempersilahkan
siswa
yang o Siswa yang belum paham
masih belum paham dengan
bertemu dengan guru.
hasil diskusi untuk bertanya.
o Menuntun siswa menyimpulkan o Membuat simpulan materi 15 menit
Penutup
materi yang telah dipelajari.
o Memberikan
yang telah dibahas.
untuk o Mengerjakan
kuis
mengetahui tingkat pemahaman
yang
diberikan.
siswa terhadap materi yang telah o Mencatat
dibahas.
kuis
tugas
yang
diberikan oleh guru.
o Memberikan pekerjaan rumah o Mendengarkan dengan baik
(PR) berupa soal-soal di LKS
dan mempersiapkan diri
siswa
untuk
yang
sesuai
dengan
materi yang di bahas.
selanjutnya.
o Menginformasikan
siswa
kepada o Memberi
bahwa
pertemuan
berikutnya akan
membahas
tentang
persamaan
pertemuan
jenis-jenis
akar
kuadrat
dan
salam
kepada
guru.
pertidaksamaan kuadrat.
IX. Penilaian Hasil Belajar
1. Penilaian proses
Afektif :
1. Dengan pengamatan langsung dikelas, guru mengamati aktivitas siswa dalam
melakukan diskusi kelompok.
2. Dengan menilai keaktifan siswa dalam diskusi kelompok pada saat mengerjakan
LKS.
Indikator dan penilaian aspek afektif siswa dalam pembelajaran sebagai berikut:
No
1
Indikator sikap
Receiving (A1)
Keterangan
Adanya
penerimaan/perhatian
siswa
terhadap guru atau mata pelajaran
2
Responding (A2)
Tumbuhnya
minat/motivasi
terhadap
pelajaran
3
Valuing (A3)
Semangat/usaha yang tinggi
4
Organizing (A4)
Tumbuhnya keyakinan, menerima konsep
5
Characterizing (A5) Jujur, disiplin, kerja keras, percaya diri,
bertanggung jawab, kreatif, mandiri
Pedoman pemberian nilai afektif sebagai berikut:
No
Criteria
Keterangan
1
Tidak mencapai A1
Kurang (nilai 2)
2
Mencapai A1 s.d. A2
Cukup (nilai 3)
3
Mencapai A3 s.d. A4
Baik (nilai 4)
4
Mencapai A5
Sangat Baik (nilai 5)
Format penilaian afektif:
No
Nama Siswa
A1
A2
A3
A4
A5
Kategori
1
2
dst
2. Kognitif :
Menilai kemampuan peserta didik dalam menyampaikan ide atau pendapat selama
proses pembelajaran.
Tes lisan (dapat berupa latihan soal atau kuis)
Tugas Individu
Penilaian Produk:
a. Teknik
: Kuis
b. Bentuk instrumen
: Uraian
c. Instrumen
:
1. Diketahui fungsi kuadrat f(x) = x2 - 2x, gambarlah grafiknya !
X. Rubrik Penskoran
No
1.
Penyelesaian
a.
Titik potong f(x) terhadap sumbu X.
Skor
20
f (x) = x2 - 2x = 0
x (x - 2) = 0
x = 0 atau x = 2
Jadi, titik potongnya adalah (0, 0) dan (2, 0).
b. Titik potong f(x) terhadap sumbu Y.
20
f (x) = f (0)
= 02 – 2.0
=0
Jadi, titik potongnya adalah (0, 0)
c. Persamaan sumbu simetrinya.
20
merupakan sumbu simetrinya.
d. Titik puncaknya.
20
-b -D
Titik puncaknya adalah (
,
) = (1, -1).
2a 4a
e. Gambar Grafiknya.
20
8
9
8
7
6
5
4
f(x) = x2 - 2x
3
2
1
-7
-6
-5
-4
-3
-2
-1
1
2
3
4
5
6
-1
-2
-3
-4
-5
Skor Maksimal
100
-6
-7
-8
Nilai akhirnya =
-9
Mengetahui/Menyetujui,
Guru pamong
Singaraja, September 2013
Mahasiswa Praktikan
Made Kartini, S.Pd
NIP. 19590321 198012 2 005
Ni Made Nur Widowati .R.
NIM. 1013011048
Mengetahui/Menyetujui,
Dosen Pembimbing
Prof. Dr. I Gusti Putu Suharta, M. Si
NIP. 19621215 198803 1 002
7
8