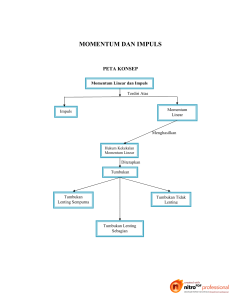
6. sistem partikel dan kekekalan momentum

Fisika Dasar I (FI-321)
Topik hari ini (minggu 6)
Sistem Partikel
dan
Kekekalan Momentum
Persoalan Dinamika
Konsep Gaya
Konsep Energi
Gaya berkaitan dengan
perubahan gerak
(Hukum Newton)
Lebih mudah pemecahannya
karena kita hanya bekerja
dengan besaranbesaran-besaran skalar
Besaran-besaran
BesaranVektor, jadi
Informasi tentang
Arah tetap
dipertahankan
Kehilangan informasi
tentang arah
Konsep
Momentum
Dan
Impuls
Besaran-besaran
BesaranVektor, jadi
Informasi tentang
Arah tetap
dipertahankan
Hk II Newton dalam Bentuk Impuls dan
Momentum
r dpr
Hk II Newton : F =
dt
Bila diketahui gaya sebagai fungsi waktu, maka Hk II Newton menjadi :
t
r
p
0
r
p0
r
r r r
r
r
∫ Fdt = ∫ dp = p − p0 = mv − mv0
t
r
r
∫ Fdt = I
0
Dikenal sebagai Impuls
dan
r
r
p = mv
Sehingga bentuk integral Hk II Newton menjadi
sebagai
momentum linier
r r r
r
I = p − p 0 = ∆p
Momentum Linier
►
Dari Hukum Newton: Gaya harus hadir untuk mengubah
kecepatan sebuah benda (laju dan/atau arah)
Ingin meninjau efek dari tumbukan dan kaitannya
dengan perubahan kecepatan
Bola golf pada awalnya
diam, energi kinetik dari
tongkat golf ditransfer
untuk menghasilkan gerak
dari bola golf (mengalami
perubahan kecepatan)
Untuk menjelaskannya digunakan konsep momentum
linier
Momentum Linier = massa
skalar
× kecepatan
vektor
Momentum (lanjutan)
p = mv
►
►
Besaran Vektor,
Vektor, arah momentum sama dengan arah
kecepatan
Diaplikasikan dalam gerak dua dimensi menjadi:
p x = mv x dan p y = mv y
Besar momentum: bergantung pada massa
bergantung pada kecepatan
Impuls
► Untuk
mengubah momentum dari sebuah benda
(misal bola golf), sebuah gaya harus dihadirkan
► Laju perubahan momentum sebuah benda sama
dengan gaya neto yang bekerja pada benda tsb
Fnet =
∆ p m( v f − v i )
=
= m a atau : ∆ p = Fnet ∆t
∆t
∆t
Memberikan pernyataan lain Hukum II Newton
(F ∆t) didefinisikan sebagai impuls
Impuls adalah besaran vektor,
vektor, arahnya sama dengan
arah gaya
Interpretasi Grafik dari Impuls
►
Biasanya gaya tidak konstan
(bergantung waktu)
impuls = ∑ Fi ∆t i = luas di bawah kurva F (t )
∆t i
►
Jika gaya tidak konstan,
gunakan gaya ratarata-rata
►
Gaya ratarata-rata dapat dikatakan
sebagai gaya konstan yang
memberikan impuls yang sama
pada benda dalam selang waktu
seperti pada gaya sebenarnya
(bergantung waktu)
Jika gaya konstan: impuls = F ∆t
Latihan 1
Sebuah benda yang bermassa 5 kg mulamula-mula bergerak dengan kecepatan
r
v 0 = 2 î + 3 ˆj m / s , kemudian mengalami gaya dengan komponen x
berubah terhadap waktu seperti pada gambar, dan komponen y yang
berubah terhadap waktu menurut F = 4 t N
y
Fx(N)
10
3
2
4
5
t (sekon)
-10
Tentukanlah:
a. Impuls yang dialami benda antara t=0 dan t=5 s!
b. Momentum linier dan kecepatannya saat t=5 s!
c. Gaya rata
rata--rata yang dialami benda selama 5 s tersebut!
Contoh: Impuls diaplikasikan
pada Mobil
► Faktor
terpenting adalah waktu benturan atau
waktu yang diperlukan pengemudi/penumpang
untuk diam
Ini akan mengurangi kemungkinan kematian pada tabrakan mobil
► Cara
untuk menambah waktu
Sabuk pengaman
Kantung udara
kantung udara menambah waktu tumbukan dan menyerap energi
dari tubuh pengemudi/penumpang
Sistem Banyak Partikel
Tinjau sistem yang terdiri dari N buah partikel, momentum total sistem
dituliskan
N
r r r
r
r
P = p1 + p 2 + ...... + p N = ∑ p i
i =1
Untuk melihat bagaimana evolusi momentum total ini,
sebagai ilustrasi kita tinjau sistem yang terdiri dari 3 partikel (N=3)
Gaya--gaya yang bekerja pada partikel 1:
Gaya
Gaya--gaya yang bekerja pada partikel 2:
Gaya
Gaya--gaya yang bekerja pada partikel 3:
Gaya
r ( e ) r ( i ) r (i )
F1 , F12 , F13
r ( e ) r ( i ) r (i )
F2 , F21 , F23
r ( e ) r ( i ) r (i )
F3 , F31 , F32
Hk II Newton partikel 1:
Hk II Newton partikel 2:
r
dp1 r (e ) r (i ) r (i )
= F1 + F12 + F13
dt
r
dp 2 r (e ) r (i ) r (i )
= F2 + F21 + F23
dt
Hk II Newton partikel 3:
r
dp 3 r (e ) r (i ) r (i )
= F3 + F31 + F32
dt
Lanjutan Sistem Banyak Partikel
Jumlahkan Hk II Newton pertikel 1, 2 dan 3:
r ( e ) r ( e ) r ( e ) r (i ) r ( i )
r ( i ) r (i )
r (i ) r ( i )
d r r r
(p1 + p 2 + p 3 ) = F1 + F2 + F3 + (F12 + F21 ) + (F13 + F31 ) + (F23 + F32 )
dt
Ruas kiri adalah laju perubahan momentum total sistem.
Di ruas kanan, gayagaya-gaya di dalam kurung adalah pasangan aksi
aksi--reaksi.
Akhirnya diperoleh:
r (e ) r (e ) r (e )
r (e )
d r d r r r
P = (p1 + p 2 + p 3 ) = F1 + F2 + F3 = ∑ F
dt
dt
Jadi, evolusi dari momentum total sistem hanya
dipengaruhi oleh gayagaya-gaya luar saja
Pusat Massa Sistem
Momentum total sistem:
r r r
r
P = p1 + p 2 + ...... + p N =
N
r
r
r
r
∑ pi = m1v1 + m2v2 + ...... + mN vN
i =1
r
r
r
r
r
r
drN d
dr1
dr2
= m1
+ m2
+ ...... + mN
= (m1r1 + m2 r2 + ...... + mN rN )
dt
dt
dt
dt
Bila Massa Total Sistem M,
N
M = m1 + m2 + ...... + mN = ∑ mi
i =1
Momentum total sistem menjadi:
r
r
r
r
r
d (m1r1 + m2 r2 + ...... + mN rN )
d r
P=M
= M R pm = MV pm
dt
M
dt
Momentum total sistem banyak partikel sama dengan momentum
sebuah partikel bermassa M (jumlah massa anggota sistem) yang
terletak di pusat massanya
Lanjutan Pusat Massa Sistem
Posisi pusat massa sistem adalah:
N
r
r
r
r
m1r1 + m2 r2 + ... + mN rN
=
R pm =
M
r Catt:
∑ mi ri
i =1
N
∑m
i =1
i
Animasi 6-1
Persamaan di samping adalah persamaan
vektor, jadi kita dapat menuliskannya
dalam bentuk komponen.
Secara fisis, pusat massa menunjukkan ratarata-rata letak massa
sistem dan juga menunjukkan posisi tempat seolahseolah-olah
massa sistem terkumpul
Untuk sistem yang terdiri dari benda kontinu, pusat massanya dapat dihitung
dengan menganggap benda terdiri dari elemenelemen-elemen kecil bermassa dm dan
notasi sigma di atas diganti dengan integrasi
r
Catt:
r
dm
r
1 r
∫
Persamaan di samping adalah persamaan
R pm =
=
r
dm
∫
M
vektor, jadi kita dapat menuliskannya
dm
∫
dalam bentuk komponen.
Latihan 2
1. Empat buah partikel dengan massa dan posisi (x,y) masingmasing-masing sebagai berikut
m1= 1 kg posisi (0 m,0 m), m2= 2 kg posisi (1 m,0 m), m3= 3 kg posisi (1 m,1 m),
dan m4= 4 kg posisi (0 m,1 m). Tentukan posisi pusat massa sistem!
2. Sebuah batang yang panjangnya 10 m terletak pada sumbu x dengan pangkal
batang pada posisi x = 0 dan ujung batang pada posisi x = 10 m. Anggap batang
hanya berdimensi satu (x), tentukan posisi pusat massanya apabila!
a. Rapat massa batang homogen
b. Rapat massa batang merupakan fungsi posisi menurut λ(x) = 6x kg/m
3. Tentukan pusat massa sepotong kawat homogen (rapat massa konstan) yang
berbentuk setengah lingkaran berjejari R!
R
Gerak Pusat Massa
Momentum total sistem:
r
r
r
r
r
d (m1r1 + m2 r2 + ...... + mN rN )
d r
P=M
= M R pm = MV pm
dt
M
dt
Hk II Newton:
(
)
r
dV pm
r
r (e )
r
d r d
P=
MV pm = M
= Ma pm = ∑ F
dt
dt
dt
Pusat massa sebuah sistem bergerak seperti sebuah partikel
bermassa M = ∑ mi di bawah pengaruh gaya eksternal
yang bekerja pada sistem
Animasi 6.2
Kekekalan Momentum
►
Definisi: sebuah sistem terisolasi adalah sistem yang tidak
dikenai gaya eksternal padanya
(
)
r
dV pm
r (e )
r
r
d r d
P=
= Ma pm = ∑ F = 0
MV pm = M
dt
dt
dt
r
d r
P = 0 ⇒ P = Konstan
dt
Momentum dalam sebuah sistem terisolasi dimana
terjadi peristiwa tumbukan adalah konstan
Tumbukan merupakan kontak fisik antara dua benda (atau lebih)
Dalam setiap tumbukan, suatu gaya yang relatif besar bekerja pada
masing--masing partikel yang bertumbukan dalam waktu yang relatif
masing
singkat
Contoh: “Kontak” dapat timbul dari interaksi eletrostatik
Kekekalan Momentum (lanjutan)
Prinsip kekekalan momentum menyatakan
bahwa ketika gaya eksternal neto yang
bekerja pada sebuah sistem yang terdiri dari
dua benda (atau lebih) yang saling
bertumbukan adalah nol, momentum total
dari sistem sebelum tumbukan adalah sama
dengan momentum total sistem setelah
tumbukan
Kekekalan Momentum (lanjutan)
►
Secara matematik (untuk sistem yang terdiri dua partikel):
r
r
r
r
m1v1i + m2 v2i = m1v1 f + m2 v2 f
Momentum adalah konstan untuk sistem benda
Sistem mencakup semua benda yang saling berinteraksi satu
dengan yang lainnya
Diasumsikan hanya gaya internal yang bekerja selama
terjadi tumbukan
Dapat digeneralisasi untuk jumlah benda lebih dari dua
Animasi 6.3
Jenis Tumbukan (lanjutan)
►
Tumbukan Elastik (Lenting Sempurna)
Momentum dan Energi kinetik kekal
►
Animasi 6.4
Tumbukan Inelastik (Tidak Lenting)
Momentum kekal sedangkan Energi kinetik tidak kekal
► Diubah
menjadi jenis energi yang lain seperti panas, suara
EK i = EK f + energi hilang
Tumbukan inelastik sempurna (tidak lenting sama sekali) terjadi
ketika setelah tumbukan benda saling menempel
Animasi 6.5
► Tidak
semua energi kinetik hilang
Tumbukan inelastik sebagian (tidak lenting sebagian), terjadi
antara elastik dan inelastik sempurna (tumbukan yang
sebenarnya)
Tumbukan 1 Dimensi
Tumbukan elastik sempurna, inelastik sempurna, inelastik sebagian
Koefisien restitusi e merupakan ukuran keelastikan suatu tumbukan,
didefinisikan sebagai rasio antara kelajuan saling menjauh relatif dan kelajuan
saling mendekat relatif
e=−
v2f − v1f
v2i − v1i
Tumbukan 2 dan 3 Dimensi
Tumbukan elastik sempurna, inelastik sempurna, inelastik sebagian
Strategi Pemecahan Masalah Tumbukan 2 & 3 Dimensi
Uraikan kekekalan momentum dalam tiap komponen
Terapkan hukum kekekalan energi untuk kasus tumbukan elastik sempurna
Latihan 3
1. Sebuah benda bermassa m1 = 2 kg bergerak dengan kecepatan v1 = (3 i) m/s.
Benda lain bermassa m2 = 4 kg bergerak dengan kecepatan v2 = (3 i + 6 j) m/s.
Kedua benda bertumbukan dan tetap bersatu setelah tumbukan. Hitunglah
a. Kecepatan kedua benda setelah bertumbukan!
b. Energi kinetik benda sebelum dan sesudah tumbukan!
2. Sebuah bola bilyar bergerak dengan kecepatan u1 = (4 i) m/s. Bola menumbuk
bola lain yang identik dalam keadaan diam. Setelah tumbukan, bola pertama
membentuk sudut 300 dengan arah semula. Bila tumbukan bersifat elastik sempurna,
tentukan kecepatan masing-masing bola setelah tumbukan.
Kerangka Acuan Pusat Massa
r
r
r
r (e )
dV pm
r
d
d
P=
MV pm = M
= Ma pm = ∑ F = 0
dt
dt
dt
r
d r
P = 0 ⇒ P = Konstan
dt
(
)
Jika gaya eksternal neto sama dengan nol, maka kecepatan pusat massa konstan
► Dipilih sistem koordinat dengan titik asal di pusat massa (Kerangka
(Kerangka acuan pusat
masa))
masa
► Kerangka acuan pusat massa dinamakan juga kerangka acuan momentum nol
►
Contoh
r
v
Sistem dua partikel, dimana m1 bergerak dengan kecepatan 1 dan m2 bergerak
r
dengan kecepatan v2 .
r
r
r
m1v1 + m2 v2
Kecepatan pusat massa: V pm =
m1 + m2
r r r
Kecepatan--kecepatan dalam kerangka pusat massa: u1 = v1 − V pm
Kecepatan
r r r
u2 = v2 − V pm
Energi Kinetik Sistem Partikel
►
Energi kinetik sistem partikel adalah jumlah energi kinetik masingmasing-masing
partikel
r
r r
r
1 r2
1 r r
1
K = ∑ mi vi = ∑ mi (vi .vi ) = ∑ mi (V pm + ui ).(V pm + ui )
i 2
i 2
i 2
r
1 r2
1 r2
= ∑ miV pm + ∑ mi ui + V pm .∑ mi ui
i 2
i 2
i
1 r2
1 r2 1 r2
1 r2
= ∑ miV pm + ∑ mi ui = MV pm + ∑ mi ui
2
i 2
i 2
i 2
►
Suku pertama adalah energi kinetik yang berhubungan dengan gerakan
pusat massa dan suku kedua adalah energi kinetik sistem partikel relatif
terhadap pusat massa
PR
Buku Tipler
Hal 258258-259 no: 52, 54, 58
Hal 260 no: 78
Gerak dengan Massa Berubah
Hukum II Newton :
r
∑ Feksternal
r
r
r
dP d
dv r dM
=
= (Mv ) = M
+v
dt dt
dt
dt
Ruas kiri menyatakan resultan gaya-gaya luar yang bekerja
pada sistem
Suku pertama ruas kanan menyatakan perubahan momentum
sistem akibat perubahan kecepatannya
Suku kedua ruas kanan menyatakan perubahan momentum
sistem akibat perubahan massanya
Dorongan Roket
► Prinsip
roket berdasarkan pada hukum
kekekalan momentum yang diaplikasikan
pada sebuah sistem, dimana sistemnya
adalah roket sendiri ditambah bahan bakar
Berbeda dengan dorongan yang terjadi di
permukaan bumi dimana dua benda saling
mengerjakan gaya satu dengan yang lain
►Jalan
pada mobil
►Rel pada kereta api
Dorongan Roket (lanjutan)
► Roket
dipercepat sebagai hasil dari
hentakan buangan gas
► Ini merepresentasikan kebalikan dari
tumbukan inelastik
Momentum kekal
Energi kinetik bertambah
Dorongan Roket (lanjutan)
Pada saat t :
m
mv
► Massa
awal roket (+ bahan bakar) adalah m
► Kecepatan awal roket adalah v
► Momentum
awal sistem Pi = m v
Dorongan Roket (lanjutan)
Pada saat t + ∆t :
m ̶ ∆m
∆m
u
►
►
►
►
Massa roket sekarang adalah adalah m ̶ ∆m
Massa gas yang keluar ∆m
Kecepatan roket bertambah menjadi v + ∆v
Momentum akhir sistem Pf = momentum roket + momentum
gas buang
Pf = (m–
(m–∆m) (v+∆v
(v+∆v)) + ∆m u
Dorongan Roket (lanjutan)
Pf - Pi = m ∆ v + ∆m[u- (v + ∆v )] = Feks ∆t
Feks
∆ v ∆m
[u- (v + ∆v )]
=m
+
∆t
∆t
∆m
dm
Limit ∆t → 0 ⇒ ∆ v → 0 dan
=−
∆t
dt
d v dm
d v dm
[u- v] = m − v relatif
Feks = m
−
dt
dt
dt
dt
dv
dm
dm d
dm
Feks = m
+v
−u
= (m v ) - u
dt
dt
dt dt
dt
Dorongan Roket (lanjutan)
Persamaan umum gerak roket :
Feks
d v dm
=m
−
v relatif
dt
dt
v relatif = Kecepatan gas yang keluar relatif terhadap roket
dm
= Laju pembakaran gas
dt
dm
v relatif = Gaya dorong
dt
Latihan
1.
Sebuah roket bergerak dalam ruang bebas tanpa medan gravitasi dengan
kecepatan awal v0= 500 i m/s. Roket menyemburkan gas dengan laju
relatif terhadap roket sebesar 1000 m/s dalam arah berlawanan gerak
roket.
a. Berapa kecepatan akhir roket ketika massanya tinggal ½ kali semula!
b. Berapa besar gaya dorong selama perjalanan bila laju pembakaran gas
10 kg/s
2.
Roket bermassa 6000 kg disiapkan untuk peluncuran vertikal. Jika laju
semburannya 1000 m/s, berapakah banyaknya gas yang harus
disemburkan tiap detik agar dapat diperoleh dorongan yang dibutuhkan
untuk:
a. mengatasi berat roket!
b. memberikan percepatan awal pada roket sebesar 20 m/s2!