kemiringan dan titik potong sumbu

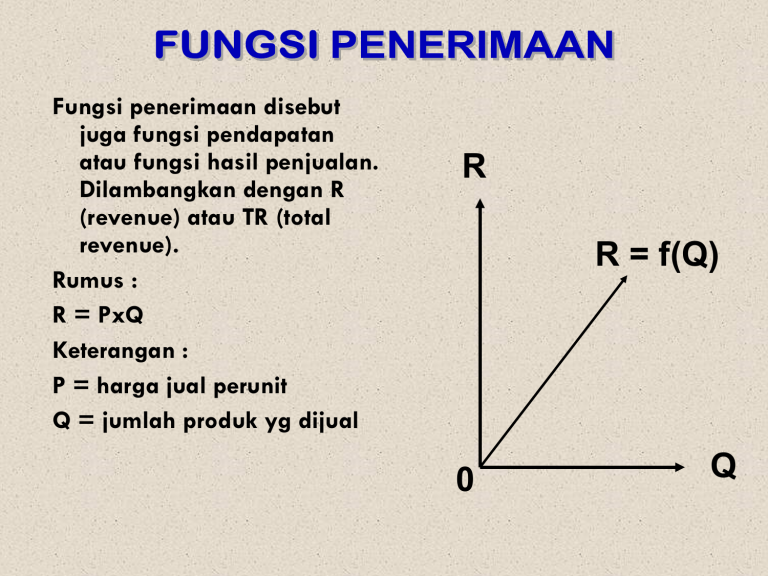
Fungsi penerimaan disebut
juga fungsi pendapatan
atau fungsi hasil penjualan.
Dilambangkan dengan R
(revenue) atau TR (total
revenue).
Rumus :
R = PxQ
Keterangan :
P = harga jual perunit
Q = jumlah produk yg dijual
R
R = f(Q)
0
Q
Contoh
Misalkan suatu produk dijual
dengan harga Rp 5.000
perunit barang.
Bagaimanakah fungsi
penerimaannya ?
Gambarkan fungsi
penerimaan tersebut pada
grafik
JAWAB :
R = PxQ
R = 5000Q
R
R = 5000Q
Q
FUNGSI BIAYA
Fungsi biaya diberi lambang C
(cost) atau TC (total cost)
Rumus :
TC = FC + VC
TC = FC + P.Q
Keterangan :
FC = fix cost = biaya tetap
VC = variabel cost
= biaya
yg berubah
FC , VC, TC
TC
VC
FC
Q
0
Contoh
Jawab :
TC = 100.000.000 + 3000Q
Sebuah perusahaan
mengeluarkan biaya tetap
sebesar Rp 100.000.000 dan
biaya variabelnya Rp.3.000
per unit barang
Tentukan fungsi biayanya ?
Gambarkan grafik fungsinya ?
TC
TC
100.
000.
000
0
Q
FUNGSI PENERIMAAN TOTAL (Bentuk Kuadrat)
Penerimaan total dari suatu perusahaan (produsen) adalah
hasil kali antara harga per unit produk dengan jumlah
produk yang dijual, atau rumusnya adalah,
TR = P . Q
dimana : TR = Penerimaan Total
Q = Jumlah produk yang dijual
P = Harga produk per unit
Jika fungsi permintaan linier dan menurun dari kiri atas ke
kanan bawah berarti harga P tidak tetap, maka
penerimaan total (TR) akan berbentuk fungsi kuadrat. Jadi,
bila fungsi permintaan dinyatakan oleh P = b – aQ, maka
akan diperoleh persamaan penerimaan total,
TR = P . Q
TR = ( b – aQ) Q
TR = bQ – aQ2
Fungsi penerimaan total bila digambarkan dalam bidang
koordinat akan berbentuk kurva parabola yang terbuka ke
bawah dan memotong sumbu Q di dua titik, yaitu : Q = 0 dan
xxx. Karena puncak yang maksimum, yaitu :
Titik Puncak
Contoh
Diketahui fungsi permintaan P = 20 – 2Q, carilah penerimaan total
maksimum dan gambarkanlah kurva dan penerimaan total dalam satu
diagram!
Penyelesaian :
TR = PQ
TR = (20 – 2Q)Q
TR = 20Q – 2Q2
2

  20  (20)
,
TR = Maksimum  

 2(2) 4(2)


  20  (400) 
,
 
  (5,50)

8 
 4

Jika TR = 0, maka 20Q – 2Q2 = 0
2Q (10–Q) = 0
Q1 = 0
Q2 = 0
Kurva penerimaan total ini ditunjukkan oleh Gambar di bawah.
P, TR
(5, 50)
50
TR = 20Q – 2Q2
40
8,30
30
2,30
(0,20) 20
10
P =20 – 2Q
(0,0)
(10,0)
0
1
2
3
4
5
6
7
8
9
10
Q